正扭歪無限面體

在幾何學中，正扭歪^[1][2]無限面體（英語：Regular skew apeirohedron），又稱扭歪正多面體（日語：ねじれ正多面体）^{[註 1]}是一種頂點並非全部共面的正無限面體，即每個面都全等、每個角也相等的扭歪無限面體。通常扭歪無限面體會具有正扭歪的面或扭歪的頂點圖。

歷史

關於考克斯特，1926年時，約翰·弗林德斯·皮特里將扭歪多邊形（非平面多邊形）的概念推廣到四維空間的扭歪多面體和三維空間的扭歪無限面體。

考克斯特找到了三種形式，他們具有平的面和扭歪的頂點圖，兩者彼此互補。它們都可以用施萊夫利符號的擴展符號{l,m|n}來表示。這個擴展符號{l,m|n}表示每個頂點都是${\displaystyle m}$個正${\displaystyle l}$邊形的公共頂點，且存在正${\displaystyle n}$邊形的空洞。

若一扭歪無限面體是一個正扭歪無限面體，則其施萊夫利符號存在下列等式：

• 2 sin(π/l) · sin(π/m) = cos(π/n)

三維空間的正扭歪無限面體

三維空間中有三種扭歪無限面體，分別為四角六片四角孔扭歪無限面體、六角四片四角孔扭歪無限面體和六角六片三角孔扭歪無限面體。約翰·康威將他們稱為多立方體（英語：Mucube）、多八面體（英語：Muoctahedron）和、多四面體（英語：Mutetrahedron），英文中的字首mu-表示「多」（英語：multiple）的意思，其意義分別代表「很多立方體」、「很多八面體」以及「很多四面體」^[3]。

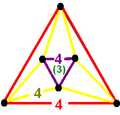
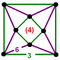
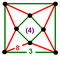
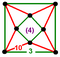
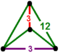
1. 四角六片四角孔扭歪無限面體（多立方體、英語：Mucube）：{4,6|4}：每個頂點都是六個正方形的公共頂點
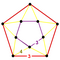
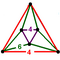
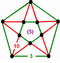
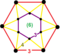
2. 六角四片四角孔扭歪無限面體（多八面體、英語：Muoctahedron）：{6,4|4}：每個頂點都是四個六邊形的公共頂點
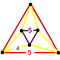
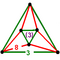
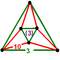
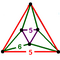
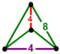
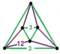
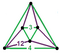
3. 六角六片三角孔扭歪無限面體（多四面體、英語：Mutetrahedron）：{6,6|3}：每個頂點都是六個六邊形的公共頂點

考克斯特給予這些 {2q,2r|p} 形式的扭歪無限面體與抽象群 (2q,2r|2,p) 同構的[[(p,q,p,r)]⁺的手徵對稱性。與之相關的堆砌就具有[[(p,q,p,r)]]的擴展對稱性^[4]。

緊空間正扭歪無限面體

考克斯特群 對稱性	無限面體 {p,q|l}	圖像	面 {p}	洞 {l}	頂點圖	相關堆砌
[[4,3,4]] [[4,3,4]+]	{4,6|4} 四角六片四角孔 扭歪無限面體 多立方體	動畫			扭歪六邊形 （黃色部分）	t0,3{4,3,4}
	{6,4|4} 六角四片四角孔 扭歪無限面體 多八面體	動畫			扭歪四邊形 （綠色部分）	2t{4,3,4}
[[3[4]]] [[3[4]]+]	{6,6|3} 六角六片三角孔 扭歪無限面體 多四面體	動畫			扭歪六邊形 （綠色部分）	q{4,3,4}（英語：Quarter cubic honeycomb）

三維雙曲空間的正扭歪無限面體

1967年時，C. W. L. Garner以類似於在歐式三維空間尋找正扭歪無限面體的方式，發現了31種雙曲空間中具有扭歪多邊形頂點圖的正扭歪無限面體^[5]。

14種緊空間正扭歪無限面體

14種緊空間正扭歪無限面體

考克斯特群	無限面體 {p,q|l}	面 {p}	洞 {l}	堆砌	頂點圖		無限面體 {p,q|l}	面 {p}	洞 {l}	堆砌	頂點圖
[3,5,3]	{10,4|3}			2t{3,5,3}（英語：Bitruncated icosahedral honeycomb）			{4,10|3}			t0,3{3,5,3}（英語：Runcinated icosahedral honeycomb）
[5,3,5]	{6,4|5}			2t{5,3,5}（英語：Bitruncated order-5 dodecahedral honeycomb）			{4,6|5}			t0,3{5,3,5}（英語：Runcinated order-5 dodecahedral honeycomb）
[(4,3,3,3)]	{8,6|3}			ct{(4,3,3,3)}			{6,8|3}			ct{(3,3,4,3)}
[(5,3,3,3)]	{10,6|3}			ct{(5,3,3,3)}			{6,10|3}			ct{(3,3,5,3)}
[(4,3,4,3)]	{8,8|3}			ct{(4,3,4,3)}（英語：Cyclotruncated cubic-octahedral honeycomb）			{6,6|4}			ct{(3,4,3,4)}（英語：Cyclotruncated octahedral-cubic honeycomb）
[(5,3,4,3)]	{8,10|3}			ct{(4,3,5,3)}			{10,8|3}			ct{(5,3,4,3)}
[(5,3,5,3)]	{10,10|3}			ct{(5,3,5,3)}（英語：Cyclotruncated dodecahedral-icosahedral honeycomb）			{6,6|5}			ct{(3,5,3,5)}（英語：Cyclotruncated icosahedral-dodecahedral honeycomb）

17種仿緊空間正扭歪無限面體

17種仿緊空間正扭歪無限面體

考克斯特群	無限面體 {p,q|l}	面 {p}	洞 {l}	堆砌	頂點圖		無限面體 {p,q|l}	面 {p}	洞 {l}	堆砌	頂點圖
[4,4,4]	{8,4|4}			2t{4,4,4}（英語：Bitruncated order-4 square tiling honeycomb）			{4,8|4}			t0,3{4,4,4}（英語：Runcinated order-4 square tiling honeycomb）
[3,6,3]	{12,4|3}			2t{3,6,3}（英語：Bitruncated triangular tiling honeycomb）			{4,12|3}			t0,3{3,6,3}（英語：Runcinated triangular tiling honeycomb）
[6,3,6]	{6,4|6}			2t{6,3,6}（英語：Bitruncated order-6 hexagonal tiling honeycomb）			{4,6|6}			t0,3{6,3,6}（英語：Runcinated order-6 hexagonal tiling honeycomb）
[(4,4,4,3)]	{8,6|4}			ct{(4,4,3,4)}			{6,8|4}			ct{(3,4,4,4)}
[(4,4,4,4)]	{8,8|4}			q{4,4,4}（英語：Order-4 square tiling honeycomb）
[(6,3,3,3)]	{12,6|3}			ct{(6,3,3,3)}			{6,12|3}			ct{(3,3,6,3)}
[(6,3,4,3)]	{12,8|3}			ct{(6,3,4,3)}			{8,12|3}			ct{(4,3,6,3)}
[(6,3,5,3)]	{12,10|3}			ct{(6,3,5,3)}			{10,12|3}			ct{(5,3,6,3)}
[(6,3,6,3)]	{12,12|3}			ct{(6,3,6,3)}			{6,6|6}			ct{(3,6,3,6)}

參見

• 扭歪多面體
• 扭歪無限面體
• 無限面體