拉梅函數

拉梅函數(Lame functions)是下列拉梅方程的解:^[1][2][3]

雅可比形式

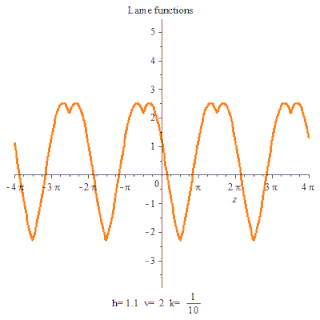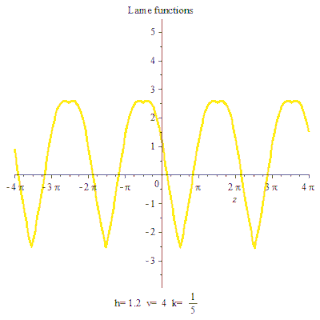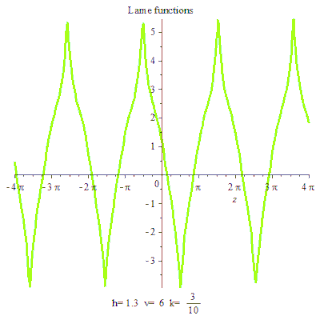Lame function Maple animation plot

${\displaystyle {\frac {d^{2}w}{dz^{2}}}+(A+v(v+1)k^{2}sn^{2}(z,k))w=0}$+ 此拉梅方程的正則奇點在複數平面的${\displaystyle 2pK+(2q+1)*iK'}$ 其中 p,q ∈Z,K代表模數為k的完全橢圓積分，K'代表模數為${\displaystyle k'={\sqrt {1-k^{2}}}}$的完全橢圓積分。

其中 k,v 都是實數，並且 ${\displaystyle 0<k<1}$,

代數形式

作雅可比橢圓函數變數替換${\displaystyle s=sn^{2}(z,k)}$得拉梅方程的代數形式：

${\displaystyle {\frac {d^{2}\Lambda }{ds^{2}}}+{\frac {1}{2}}*({\frac {1}{2}}+{\frac {1}{s-1}}+{\frac {1}{s-h}})*{\frac {d\Lambda }{ds}}-{\frac {n(n+1)s+H}{4s(s-1)(s-h)}}*\Lambda =0}$

${\displaystyle h=k^{-2}={\frac {a^{2}-c^{2}}{a^{2}-b^{2}}}}$,

${\displaystyle H=hA}$

${\displaystyle h>1}$ 此傅克型方程有四個正則奇點${\displaystyle 0,1,h,\infty }$

魏爾斯特拉斯形式^[3]

${\displaystyle {\frac {d^{2}\Lambda }{dz^{2}}}+[H-n(n+1)\wp (z)]\Lambda =0}$

其中${\displaystyle \wp }$是魏爾斯特拉斯函數

三角函數形式

在雅可比形式的拉梅方程中做代換^[4] ${\displaystyle snz=cos\zeta }$

${\displaystyle \zeta ={\frac {1}{2}}\pi -amz}$

可得

${\displaystyle [1-(kcos\zeta )^{2}]{\frac {d^{2}\Lambda }{d\Lambda ^{2}}}}$${\displaystyle +k^{2}cos\zeta \sin \zeta {\frac {d\Lambda }{d\zeta }}+[h-n(n+1)(kcos\zeta )^{2}]\Lambda =0}$

在上列方程組 ${\displaystyle h,k,n}$等是實數或複數常數，而各變量為複數。

拉梅方程的本徵值

對於給定的參數v,k,存在四套實數本徵值h,令拉梅方程的奇數解或偶數解有2K或4K周期^[5]。

本徵值 h	奇偶	周期
${\displaystyle a_{v}^{2m}(k^{2})}$	偶	2K
${\displaystyle a_{v}^{2m+1}(k^{2})}$	奇	4K
${\displaystyle b_{v}^{2m}(k^{2})}$	偶	4K
${\displaystyle b_{v}^{2m+1}(k^{2})}$	奇	2K

拉梅函數

與每一個本徵值對應的本徵函數，稱為v階拉梅函數，其記法及周期性列表於下：^[6]

本徵值 h	奇偶	周期	本徵函數(拉梅函數)
${\displaystyle a_{v}^{2m}(k^{2})}$	偶	2K	${\displaystyle Ec_{v}^{2m}(z,k^{2})}$
${\displaystyle a_{v}^{2m+1}(k^{2})}$	奇	4K	${\displaystyle Ec_{v}^{2m+1}(z,k^{2})}$
${\displaystyle b_{v}^{2m}(k^{2})}$	偶	4K	${\displaystyle Es_{v}^{2m+1}(z,k^{2})}$
${\displaystyle b_{v}^{2m+1}(k^{2})}$	奇	2K	${\displaystyle Es_{v}^{2m+2}(z,k^{2})}$

其中${\displaystyle 2m,2m+1,2m+2}$代表在（0,2K)區間內的零點數。

拉梅函數是Heun函數的特例

Heun方程 ${\displaystyle gh:={\frac {d^{2}(y(z)}{dz^{2}}}+({\frac {\gamma }{z}}+{\frac {\delta }{z-1}}+{\frac {\epsilon }{z-a}})*{\frac {d(y(z)}{dz}}+(\alpha *\beta *z-q)*y(z)/(z*(z-1)*(z-a))=0}$

令=${\displaystyle \gamma =1/2,\delta =1/2,\epsilon =1/2,q=-(1/4)*a*h,\alpha =1/4,\beta =-v(v+1)}$

則化為拉梅方程

${\displaystyle {\frac {d^{2}(y(z)}{dz^{2}}}+(1/2*(1/z+1/(z-1)+1/(z-a)))*{\frac {d(y(z)}{dz}}+(1/4)*(a*h-\nu *(\nu +1)*z)*y(z)/(z*(z-1)*(z-a))=0}$

拉梅方程的Heun函數解

由於拉梅方程式是Heun方程的特例，因此拉梅方程可以用HeunG函數表示^[7] ${\displaystyle y(z)=_{C}1*HeunG(a,-(1/4)*a*h,-(1/2)*\nu ,(1/2)*\nu +1/2,1/2,1/2,z)}$

${\displaystyle +_{C}2*{\sqrt {(}}z)*HeunG(a,1/4+(1/4*(-h+1))*a,1+(1/2)*\nu ,1/2-(1/2)*\nu ,3/2,1/2,z)}$ 其中二個HeunG函數是線性無關的。

拉梅函數的冪級數展開

拉梅函數可以展開成冪級數形式^[8]

${\displaystyle y(z)=\sum _{v=0}^{\infty }a_{v}*z^{\rho +v}}$

其中${\displaystyle \rho }$只能取${\displaystyle 0,1/2}$

例子

${\displaystyle y(z)={1.2+2.3*{\sqrt {(}}z)-.600*h*z-(.383*(a*h-1.*a-1.))*z^{(}3/2)/a+(0.500e-1*(-4.*a*h-4.*h+a*h^{2}+2.*\nu ^{2}+2.*\nu ))*z^{2}/a+(0.192e-1*(-10.*a^{2}*h+9.*a^{2}+6.*a-10.*a*h+9.+a^{2}*h^{2}+6.*\nu *a+6.*\nu ^{2}*a))*z^{(}5/2)/a^{2}+O(z^{3})}}$