热门问题
时间线
聊天
视角
有界函數
来自维基百科,自由的百科全书
Remove ads
在數學中,如果在某個集合上定義的具有實數或複數值的某個函數的值域是有界集合,則函數被稱為有界的(或有界函數)。換句話說,存在實數,使得對於集合中的所有,都有。有時,如果對於集合中的所有,都有,則函數稱為上有界的,就是它的一個上界;如果對於集合中的所有,都有,則函數稱為下有界的,就是它的一個下界。
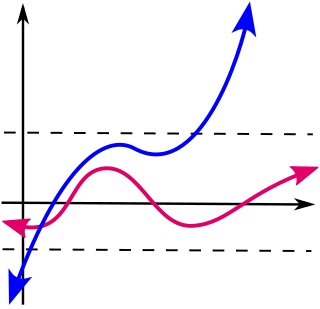
一個特例是有界數列,其中是所有自然數所組成的集合。所以,一個數列 是有界的,如果存在一個數,使得對於所有的自然數,都有。
Remove ads
例子
- 由所定義的函數是有界的。如果正弦函數是定義在所有複數的集合上,則不再是有界的。
- 函數(不等於−1或1)是無界的。當越來越接近−1或1時,函數的值就變得越來越大。但是,如果把函數的定義域限制為,則函數就是有界的。
- 函數是有界的。
Remove ads
參見
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads



















![{\displaystyle f:[0,1]\rightarrow R}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f07e139ee2aaa7c0d9233199f0c6ca7876b65bd6)