热门问题
时间线
聊天
视角
正弦-戈爾登方程
来自维基百科,自由的百科全书
Remove ads
正弦-戈爾登方程是十九世紀發現的一種偏微分方程:

來自下面的拉量:
由於正弦-戈爾登方程有多種孤立子解而倍受矚目。
Remove ads
孤立子解
 |
 |
Remove ads
正弦-戈爾登方程有如下孤立子解:
其中
 |
 |
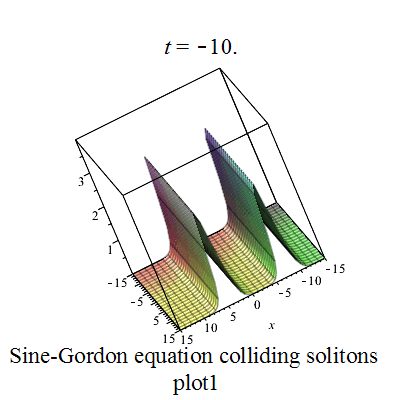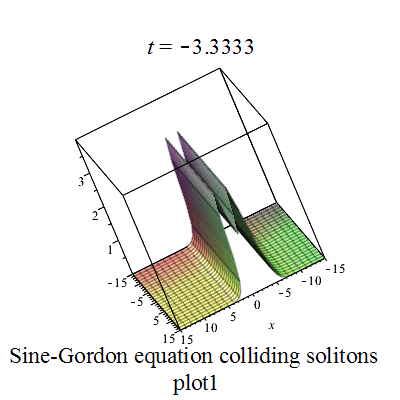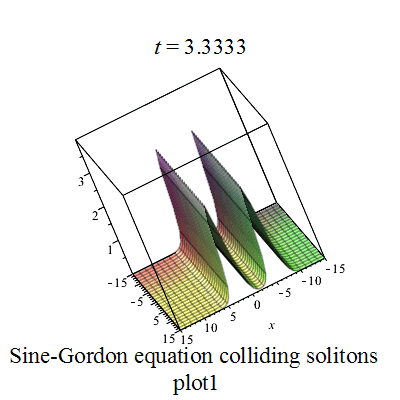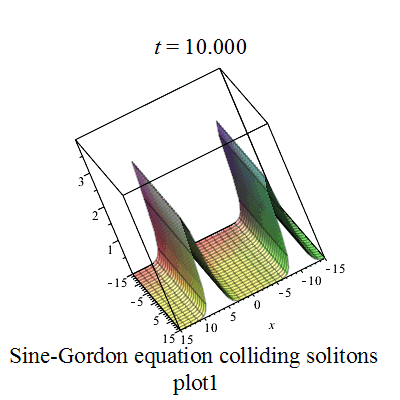 |
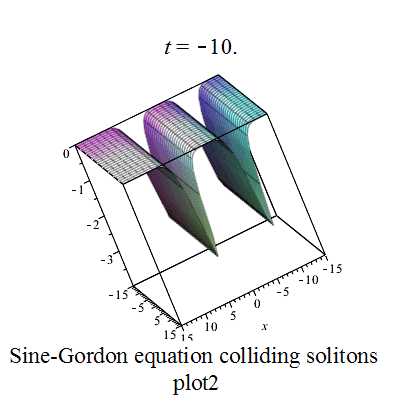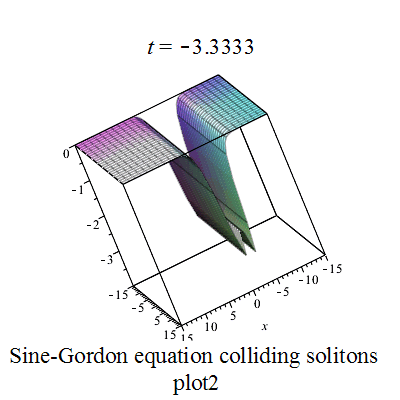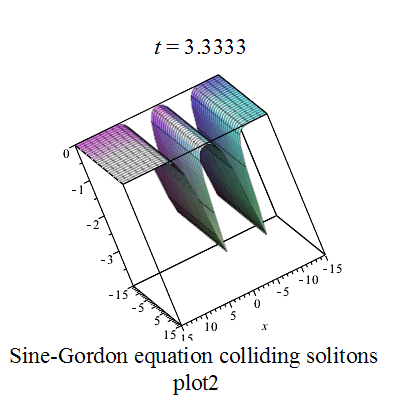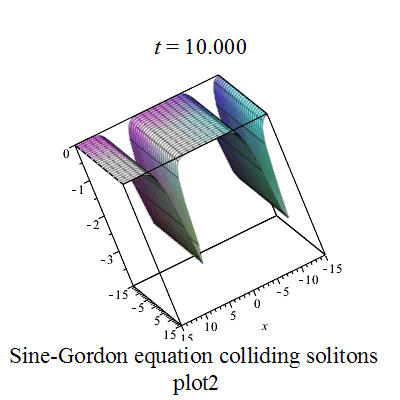 |
 |
 |
 |
 |
 |
  |
Remove ads
 |
 |
呼吸子解

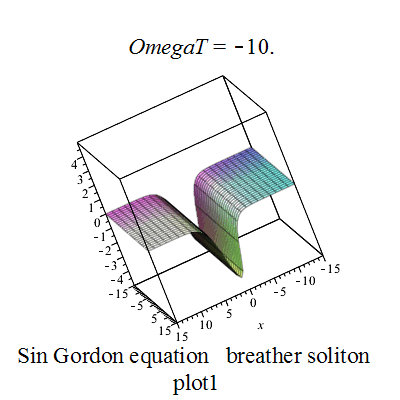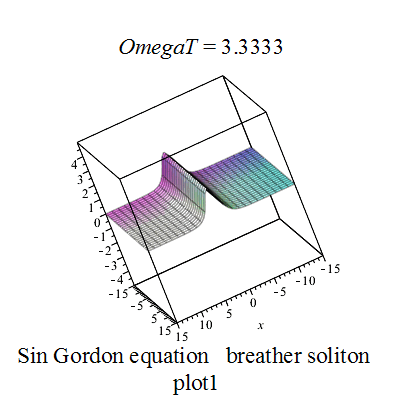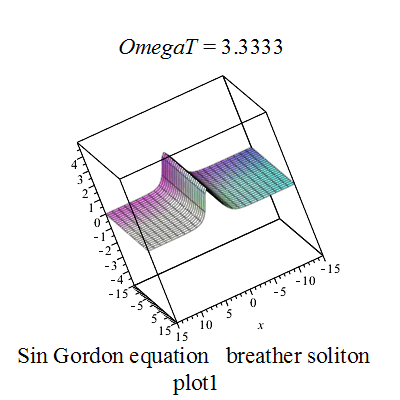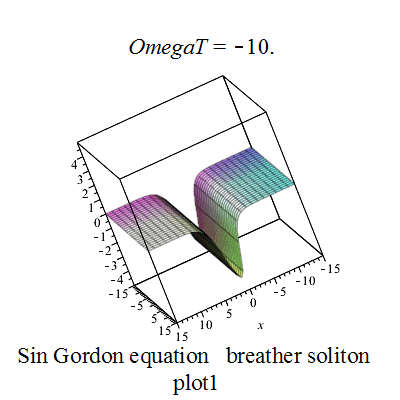 |
 |
Remove ads
幾何解釋

根據陳省身的研究,正弦-戈爾登方程有一個幾何解釋:三維歐幾里德空間的負常曲率曲面(偽球面)。[3]
正弦-戈爾登方程是:[4]
跟戶田場論有關。[5]
Remove ads
量子場論
正弦-戈爾登是Thirring模特的S對偶。
半經典量子化:[6]
參見
參考文獻
閱讀
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads












