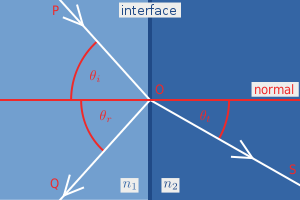
 菲涅耳方程式中所用的變量
菲涅耳方程式中所用的變量在右圖中,入射光線PO到達兩種介質交界面上的點O時,部分光線被反射,反射光為OQ,而另一部分被折射,折射光為OS。定義入射光線、反射光線和折射光線各自與法線形成的夾角分別為 、
、 和
和 。
。
入射角與反射角之間的關係由反射定律給出:

入射角與折射角之間的關係由折射定律給出。 普適的折射定律是:[1]

其中n是折射率, 是消光係數。對於無吸收損耗介質,
是消光係數。對於無吸收損耗介質, ,折射定律在此特殊情況下就是司乃耳定律:
,折射定律在此特殊情況下就是司乃耳定律:

雖然目前教科書還用複數司乃耳定律來描述損耗介質中的折射,但最近的理論和實驗已經驗證它是無效的,不能正確描述和模擬電磁波在有吸收損耗介質參與的界面的反射和折射[1]。
一定功率的入射光被界面反射的功率比例稱為反射率(反射比) ;折射的功率比例稱為透射率(透射比)
;折射的功率比例稱為透射率(透射比) [2]。對反射比和透射比的計算需要用到電動力學中的電磁波傳播理論,具體方法可參考玻恩的《光學原理:光的傳播、干涉和繞射的電磁理論》[3]以及傑克遜的《古典電動力學》[4]。
[2]。對反射比和透射比的計算需要用到電動力學中的電磁波傳播理論,具體方法可參考玻恩的《光學原理:光的傳播、干涉和繞射的電磁理論》[3]以及傑克遜的《古典電動力學》[4]。
反射比和透射比的具體形式還與入射光的偏振有關。如果入射光的電向量垂直於右圖所在平面(即s偏振),反射比為

其中 是由折射定律從
是由折射定律從 導出的。如果是無吸收損耗,還可用三角恆等式化簡。
導出的。如果是無吸收損耗,還可用三角恆等式化簡。
如果入射光的電向量位於右圖所在平面內(即p偏振),反射比為

透射比無論在哪種情況下,都有 。
。
如果入射光是無偏振的(含有等量的s偏振和p偏振),反射比是兩者的算數平均值: 。
。
反射和折射光波的振幅與入射光波振幅的比值(通常稱為反射係數和透射係數)也可用類似的方程式給出,這些方程式也稱作菲涅耳方程式:
 ,
,
 ,
,
 ,
,

根據不同的體系和符號習慣,它們可以有不同形式。反射係數和透射係數通常用小寫的  和
和  表示。在某些體系中,它們滿足條件:
表示。在某些體系中,它們滿足條件:

 [5]
[5]
對於給定的折射率 和
和 且入射光為p偏振光時,當入射角為某一定值時
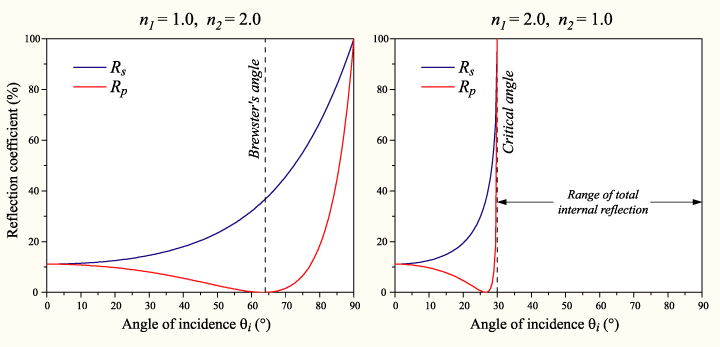
且入射光為p偏振光時,當入射角為某一定值時 為零(無吸收損耗的情況),此時p偏振光被完全透射而無反射光出射。這個角度被稱作布魯斯特角,對於空氣或真空中的玻璃介質約為56°。注意
為零(無吸收損耗的情況),此時p偏振光被完全透射而無反射光出射。這個角度被稱作布魯斯特角,對於空氣或真空中的玻璃介質約為56°。注意 為零只是對於兩種折射率都為實數的介質才有可能,對於會吸光的物質,例如金屬和半導體,折射率是一個複數,從而
為零只是對於兩種折射率都為實數的介質才有可能,對於會吸光的物質,例如金屬和半導體,折射率是一個複數,從而 的最小值一般不為零。
的最小值一般不為零。
當光從光密介質向光疏介質傳播時(即 時),存在一個臨界的入射角,對於大於此入射角的入射光
時),存在一個臨界的入射角,對於大於此入射角的入射光 ,此時入射光完全被界面反射。這種現象稱作全內反射,臨界角被稱作全反射臨界角,對於空氣中的玻璃約為41°。
,此時入射光完全被界面反射。這種現象稱作全內反射,臨界角被稱作全反射臨界角,對於空氣中的玻璃約為41°。
當光線以近法線入射( )時,反射比和透射比分別為:
)時,反射比和透射比分別為:


對於普通的玻璃,反射比大約為4%。注意窗戶對光波的反射包括前面一層以及後面一層,因而少量光波會在兩層之間來回振盪形成干涉。如忽略這種干涉效應,這兩層合併後的反射比為 (見下)。
(見下)。
需要指出的是這裡所有的討論都假設介質的磁導率 都等於真空磁導率
都等於真空磁導率 。對於大多數介電質而言這是近似正確的,但對其他類型的物質來說不正確,因而若考慮這一點則菲涅耳方程式的形式會更加複雜。
。對於大多數介電質而言這是近似正確的,但對其他類型的物質來說不正確,因而若考慮這一點則菲涅耳方程式的形式會更加複雜。