| 描述 |
圖形 |
轉動慣量 |
註解
|
| 質點,離軸距離為r,質量為m |
 |
 |
—
|
| 兩端開通的薄圓柱殼,半徑為r,質量為m |
 |
 [1] [1] |
此表示法假設了殼的厚度可以忽略不計。此為下一個物體,當其r1 = r2時的特例。
|
| 兩端開通的厚圓柱,內半徑為r1,外半徑為r2,高為h,質量為m
|
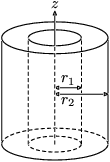
|

![{\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left[3\left({r_{1}}^{2}+{r_{2}}^{2}\right)+h^{2}\right]}](//wikimedia.org/api/rest_v1/media/math/render/svg/9e48edde3cc6fa2d6c3d6c4bbc9bf9b370269606)
或者定義標準化厚度tn = t/r並定義r = r2,
可得 |
—
|
| 實心圓柱,半徑為r,高為h,質量為m
|
 |
 [1] [1]
 |
此為前面物體,當其r1 = 0時的特例。
|
| 薄圓盤,半徑為r,質量為m |
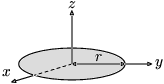 |

 |
此為前面物體,當其h = 0時的特例。
|
| 圓環,半徑為r,質量為m |
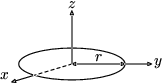 |

 |
此為後面環面,當其b = 0時的特例。
|
| 球殼,內半徑為r1,外半徑為r2,質量為m |
 |
 [1] [1] |
—
|
| 實心球,半徑為r,質量為m |
 |
 [1] [1] |
此為前面物體,當其r1 = 0時的特例;也是後面橢球,當其a = b = c時的特例。
|
| 空心球,半徑為r,質量為m |
 |
 |
此為前面球殼,當其r1 → r2時的極限。
|
| 橢球,半軸為a、b、c,質量為m |
 |


 |
—
|
| 圓錐,半徑為r,高為h,質量為m |
 |
 [2] [2]
 [2] [2] |
—
|
| 實心長方體,高為h,寬為w,長為d,質量為m |
 |


 |
邊長為 的立方體對任意過質心的軸的轉動慣量 的立方體對任意過質心的軸的轉動慣量 。 。
|
| 正四面體,邊長為s,質量為m |
 |

 [3] [3] |
「solid」意為實心,「hollow」意為空心,下同。
|
| 正八面體,邊長為s,質量為m |
 |
 [3] [3]
 [3] [3] |
—
|
| 細棒,長為L,質量為m |
 |
 [1] [1] |
此表示法假設了棒的寬度和厚度可以忽略不計。此為前面實心長方體,當其w = L,h = d = 0時的特例。
|
| 細棒,長為L,質量為m |
 |
 [1] [1] |
此表示法假設了棒的寬度和厚度可以忽略不計。
|
| 環面,圓管的半徑為a,截面的半徑為b,質量為m |
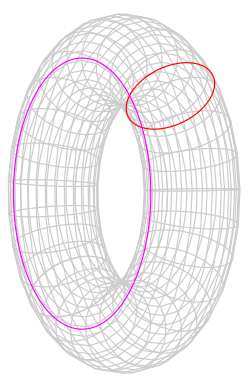 |
關於直徑: [4] [4]
關於縱軸: |
—
|
薄多邊形,頂點為 , , , , ,……, ,……, ,質量為 ,質量為 |
 |
 |
外接圓半徑為R,質量為m的正n邊形,對過其中心且垂直於所在平面的軸的轉動慣量 [5] [5]
|

 ,
, 



![{\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left[3\left({r_{1}}^{2}+{r_{2}}^{2}\right)+h^{2}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9e48edde3cc6fa2d6c3d6c4bbc9bf9b370269606)


















































 ,
,  ...
...











