邏輯運算子

在形式邏輯中，邏輯運算子或邏輯聯結詞把語句連接成更複雜的複雜語句。例如，假設有兩個邏輯命題，分別是「正在下雨」和「我在屋裡」，我們可以將它們組成複雜命題「正在下雨，並且我在屋裡」或「沒有正在下雨」或「如果正在下雨，那麼我在屋裡」。一個將兩個語句組成的新的語句或命題叫做複合語句或複合命題。又稱邏輯運算子(Logical Operators)。

基本運算子

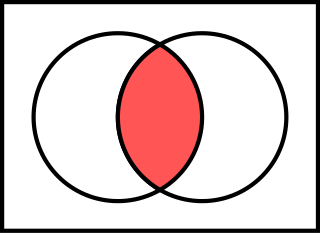
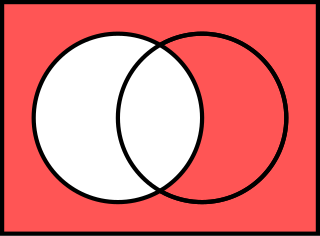
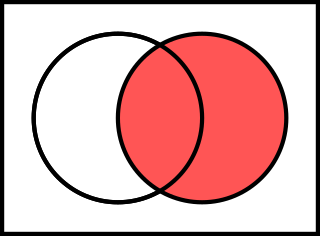
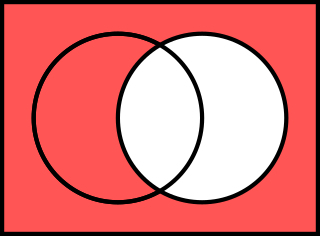
基本的運算子有：「非」（¬）、「與」（∧）、「或」（∨）、「條件」（→）以及「雙條件」（↔）。「非」是一個一元運算子，它只操作一項（¬ P）。剩下的是二元運算子，操作兩項來組成複雜語句（P ∧ Q, P ∨ Q, P → Q, P ↔ Q）。

注意，符號「與」（∧）和交集（∩），「或」（∨）和聯集（∪）的相似性。這不是巧合：交集的定義使用「與」，聯集的定義是用「或」。

這些連接符的真值表:

P	Q	¬P	P ∧ Q	P ∨ Q	P → Q	P ↔ Q
T	T	F	T	T	T	T
T	F	F	F	T	F	F
F	T	T	F	T	T	F
F	F	T	F	F	T	T

為了減少需要的括號的數量，有以下的優先規則：¬高於∧，∧高於∨，∨高於→。例如，P ∨ Q ∧ ¬ R → S是 (P ∨ (Q ∧ (¬ R)) → S的簡便寫法。

二元邏輯聯結詞表

下面是在輸入P和Q上的16個二元布林函數。

永假 符號 等價公式 真值表 文氏圖 ${\displaystyle \bot }$ P ${\displaystyle \wedge }$ ¬P   Q 0 1 P 0    0   0  1    0   0	永真 符號 等價公式 真值表 文氏圖 ${\displaystyle \top }$ P ${\displaystyle \vee }$ ¬P   Q 0 1 P 0    1   1  1    1   1
合取 符號 等價公式 真值表 文氏圖 P ${\displaystyle \wedge }$ Q P & Q P · Q P AND Q P ${\displaystyle \not \rightarrow }$¬Q ¬P ${\displaystyle \not \leftarrow }$ Q ¬P ${\displaystyle \downarrow }$ ¬Q   Q 0 1 P 0    0   0  1    0   1	與非 符號 等價公式 真值表 文氏圖 P ↑ Q P | Q P NAND Q P → ¬Q ¬P ← Q ¬P ∨ ¬Q   Q 0 1 P 0    1   1  1    1   0
非蘊涵 符號 等價公式 真值表 文氏圖 P ${\displaystyle \not \rightarrow }$ Q P ${\displaystyle \not \supset }$ Q P & ¬Q ¬P ↓ Q ¬P ${\displaystyle \not \leftarrow }$ ¬Q   Q 0 1 P 0    0   0  1    1   0	蘊涵 符號 等價公式 真值表 文氏圖 P → Q P ${\displaystyle \supset }$ Q P ↑ ¬Q ¬P ∨ Q ¬P ← ¬Q   Q 0 1 P 0    1   1  1    0   1
命題P 符號 等價公式 真值表 文氏圖 P   Q 0 1 P 0    0   0  1    1   1	非P 符號 等價公式 真值表 文氏圖 ¬P ~P   Q 0 1 P 0    1   1  1    0   0
反非蘊涵 符號 等價公式 真值表 文氏圖 P ${\displaystyle \not \leftarrow }$ Q P ${\displaystyle \not \subset }$ Q P ↓ ¬Q ¬P & Q ¬P ${\displaystyle \not \rightarrow }$ ¬Q   Q 0 1 P 0    0   1  1    0   0	反蘊涵 符號 等價公式 真值表 文氏圖 P ${\displaystyle \leftarrow }$ Q P ${\displaystyle \subset }$ Q P ∨ ¬Q ¬P ↑ Q ¬P → ¬Q   Q 0 1 P 0    1   0  1    1   1
命題Q 符號 等價公式 真值表 文氏圖 Q   Q 0 1 P 0    0   1  1    0   1	非Q 符號 等價公式 真值表 文氏圖 ¬Q ~Q   Q 0 1 P 0    1   0  1    1   0
互斥或 符號 等價公式 真值表 文氏圖 P ${\displaystyle \not \leftrightarrow }$ Q P ${\displaystyle \not \equiv }$ Q P ${\displaystyle \oplus }$ Q P XOR Q P ↔ ¬Q ¬P ↔ Q ¬P ${\displaystyle \not \leftrightarrow }$ ¬Q   Q 0 1 P 0    0   1  1    1   0	雙條件 符號 等價公式 真值表 文氏圖 P ↔ Q P ≡ Q P XNOR Q P IFF Q P ${\displaystyle \not \leftrightarrow }$ ¬Q ¬P ${\displaystyle \not \leftrightarrow }$ Q ¬P ↔ ¬Q   Q 0 1 P 0    1   0  1    0   1
析取 符號 等價公式 真值表 文氏圖 P ∨ Q P ∨ Q P OR Q P ${\displaystyle \leftarrow }$ ¬Q ¬P → Q ¬P ↑ ¬Q   Q 0 1 P 0    0   1  1    1   1	或非 符號 等價公式 真值表 文氏圖 P ↓ Q P NOR Q P ${\displaystyle \not \leftarrow }$ ¬Q ¬P ${\displaystyle \not \rightarrow }$ Q ¬P ∧ ¬Q   Q 0 1 P 0    1   0  1    0   0

圖示

真值表		哈斯圖