馬丟函數

馬丟函數（法語：Équation de Mathieu）是1868年法國數學家以米里迂·拉·馬丟（法語：Émile Mathieu）因研究數學物理所推得的特殊函數，下列馬丟方程的解析解：

${\displaystyle {\frac {d^{2}y}{dx^{2}}}+[a-2q\cos(2x)]y=0.}$

MathieuCE 3D

MathieuSE 3D

馬丟方程有兩個線性無關的解：

奇數解

MathieuCE(n, q, x)，或記為${\displaystyle w_{I}(n,q,x)}$,

偶數解

MathieuSE(n, q, x).或記為${\displaystyle w_{II}(n,q,x)}$ 稱為基本解^[1]

周期性

馬丟函數 MathieuC(a,q,z) 或 MathieuS(a,q,z) 只有一個是周期為 ${\displaystyle \pi }$ 或${\displaystyle 2\pi }$的周期解，另一個不是。

馬丟函數 MathieuC(a,q,z) 和 MathieuS(a,q,z) 兩者都有是周期為${\displaystyle 2n\pi }$（n≥2)的周期函數。 ^[1]

• 
• 
• 
• 

正交性

• ${\displaystyle \int _{0}^{2*\pi }\!ce_{m}(x,q)*ce_{n}(x,q)\,dx=0}$
• ${\displaystyle \int _{0}^{2*\pi }\!ce_{m}(x,q)*se_{n}(x,q)\,dx=0}$
• ${\displaystyle \int _{0}^{2*\pi }\!se_{m}(x,q)*se_{n}(x,q)\,dx=0}$

特徵方程

Mathieu Eigen value a(n,q)

Mathieu eigenvalue b(n,q)

馬丟方程的特徵方程是^[1]

${\displaystyle cos(\pi *v)=w_{I}(a,q,\pi )}$

${\displaystyle cos(\pi *v)=w_{II}(b,q,\pi )}$

對於給定的v，q, 上列特徵方程給出無窮多個a、b解稱為特徵值。

特徵值的展開

馬丟函數體特徵值可展開成級數：^[2]

${\displaystyle a_{0}(q)={-(1/2)*z^{2}+(7/128)*z^{4}-(29/2304)*z^{6}+(68687/18874368)*z^{8}+{\mathcal {O}}(z^{10})}}$ ${\displaystyle a_{1}(q)={1+z-(1/8)*z^{2}-(1/64)*z^{3}-(1/1536)*z^{4}+(11/36864)*z^{5}+(49/589824)*z^{6}+(55/9437184)*z^{7}-(83/35389440)*z^{8}-(12121/15099494400)*z^{9}+{\mathcal {O}}(z^{10})}}$ ${\displaystyle a_{2}(q)={4+(5/12)*z^{2}-(763/13824)*z^{4}+(1002401/79626240)*z^{6}-(1669068401/458647142400)*z^{8}+{\mathcal {O}}(z^{10})}}$ ${\displaystyle a_{3}(q)={9+(1/16)*z^{2}+(1/64)*z^{3}+(13/20480)*z^{4}-(5/16384)*z^{5}-(1961/23592960)*z^{6}-(609/104857600)*z^{7}+(4957199/2113929216000)*z^{8}+(872713/1087163596800)*z^{9}+{\mathcal {O}}(z^{10})}}$

${\displaystyle b_{1}(q)={1-z-(1/8)*z^{2}+(1/64)*z^{3}-(1/1536)*z^{4}-(11/36864)*z^{5}+(49/589824)*z^{6}-(55/9437184)*z^{7}-(83/35389440)*z^{8}+(12121/15099494400)*z^{9}+{\mathcal {O}}(z^{10})}}$ ${\displaystyle b_{2}(q)={4-(1/12)*z^{2}+(5/13824)*z^{4}-(289/79626240)*z^{6}+(21391/458647142400)*z^{8}+{\mathcal {O}}(z^{10})}}$ ${\displaystyle b_{3}(q)={9+(1/16)*z^{2}-(1/64)*z^{3}+(13/20480)*z^{4}+(5/16384)*z^{5}-(1961/23592960)*z^{6}+(609/104857600)*z^{7}+(4957199/2113929216000)*z^{8}-(872713/1087163596800)*z^{9}+{\mathcal {O}}(z^{10})}}$ ${\displaystyle b_{4}(q)={16+(1/30)*z^{2}-(317/864000)*z^{4}+(10049/2721600000)*z^{6}-(93824197/2006581248000000)*z^{8}+{\mathcal {O}}(z^{10})}}$ ${\displaystyle b_{5}(q)={25+(1/48)*z^{2}+(11/774144)*z^{4}-(1/147456)*z^{5}+(37/891813888)*z^{6}+(7/339738624)*z^{7}+(63439/201364441399296)*z^{8}+(1/2130840649728)*z^{9}+{\mathcal {O}}(z^{10})}}$

級數展開

馬丟函數ce,se的級數展開^[3]

${\displaystyle ce_{0}(z,q)={1-(1/2)*cos(2*z)*q+(-1/16+(1/32)*cos(4*z))*q^{2}+((11/128)*cos(2*z)-(1/1152)*cos(6*z))*q^{3}+O(q^{4})}}$ ${\displaystyle ce_{1}(z,q)={cos(z)-(1/8)*cos(3*z)*q+(-(1/128)*cos(z)-(1/64)*cos(3*z)+(1/192)*cos(5*z))*q^{2}+(-(1/512)*cos(z)+(1/3072)*cos(3*z)+(1/1152)*cos(5*z)-(1/9216)*cos(7*z))*q^{3}+O(q^{4})}}$ ${\displaystyle ce_{2}(z,q)={cos(2*z)+(1/4-(1/12)*cos(4*z))*q+(-(19/288)*cos(2*z)+(1/384)*cos(6*z))*q^{2}+(-49/1152+(11/4608)*cos(4*z)-(1/23040)*cos(8*z))*q^{3}+O(q^{4})}}$ ${\displaystyle ce_{3}(z,q)={cos(3*z)+((1/8)*cos(z)-(1/16)*cos(5*z))*q+(-(5/512)*cos(3*z)+(1/64)*cos(z)+(1/640)*cos(7*z))*q^{2}+(-(1/512)*cos(3*z)-(1/4096)*cos(z)+(11/40960)*cos(5*z)-(1/46080)*cos(9*z))*q^{3}+O(q^{4})}}$ ${\displaystyle ce_{4}(z,q)={cos(4*z)+((1/12)*cos(2*z)-(1/20)*cos(6*z))*q+(-(17/3600)*cos(4*z)+1/192+(1/960)*cos(8*z))*q^{2}+((7/28800)*cos(2*z)+(29/288000)*cos(6*z)-(1/80640)*cos(10*z))*q^{3}+O(q^{4})}}$

${\displaystyle se_{1}(z,q)={sin(z)-(1/8)*sin(3*z)*q+(-(1/128)*sin(z)+(1/64)*sin(3*z)+(1/192)*sin(5*z))*q^{2}+((1/512)*sin(z)+(1/3072)*sin(3*z)-(1/1152)*sin(5*z)-(1/9216)*sin(7*z))*q^{3}+O(q^{4})}}$ ${\displaystyle se_{2}(z,q)={sin(2*z)-(1/12)*sin(4*z)*q+(-(1/288)*sin(2*z)+(1/384)*sin(6*z))*q^{2}+((1/1536)*sin(4*z)-(1/23040)*sin(8*z))*q^{3}+O(q^{4})}}$ ${\displaystyle se_{3}(z,q)={sin(3*z)+((1/8)*sin(z)-(1/16)*sin(5*z))*q+(-(5/512)*sin(3*z)-(1/64)*sin(z)+(1/640)*sin(7*z))*q^{2}+((1/512)*sin(3*z)-(1/4096)*sin(z)+(11/40960)*sin(5*z)-(1/46080)*sin(9*z))*q^{3}+O(q^{4})}}$ ${\displaystyle se_{4}(z,q)={sin(4*z)+((1/12)*sin(2*z)-(1/20)*sin(6*z))*q+(-(17/3600)*sin(4*z)+(1/960)*sin(8*z))*q^{2}+(-(1/1600)*sin(2*z)+(29/288000)*sin(6*z)-(1/80640)*sin(10*z))*q^{3}+O(q^{4})}}$ ${\displaystyle se_{5}(z,q)={sin(5*z)+((1/16)*sin(3*z)-(1/24)*sin(7*z))*q+(-(13/4608)*sin(5*z)+(1/384)*sin(z)+(1/1344)*sin(9*z))*q^{2}+(-(7/73728)*sin(3*z)+(13/258048)*sin(7*z)-(1/9216)*sin(z)-(1/129024)*sin(11*z))*q^{3}+O(q^{4})}}$

傅立葉展開式

馬丟函數的傅立葉展開：^[3]

• ${\displaystyle MathieuCE(2n,q,x)=\sum _{m=0}^{\infty }A_{2m}^{2n}(q)cos(2mx)}$
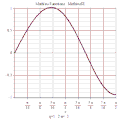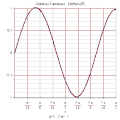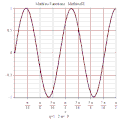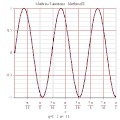
• ${\displaystyle MathieuCE(2n+1,q,x)=\sum _{m=0}^{\infty }A_{2m+1}^{2n+1}(q)cos[(2m+1)x]}$
• ${\displaystyle MathieuSE(2n+1,q,x)=\sum _{m=0}^{\infty }B_{2m+1}^{2n+1}(q)sin[(2m+1)x]}$
• ${\displaystyle MathieuSE(2n+2,q,x)=\sum _{m=0}^{\infty }B_{2m+2}^{2n+2}(q)sin[(2m+2)x]}$

其中係數A,B滿足下列遞歸關係：^[3]

${\displaystyle aA_{0}=qA_{2}}$

${\displaystyle (a-4)A_{2}=q(2A_{0}+A_{4})}$

${\displaystyle (a-4m^{2})A_{2m}=q(A_{2m-2}+A_{2m+2})}$

${\displaystyle (a-1+q)B_{1}=qB_{3}}$

${\displaystyle (a-(2m+1)^{2})B_{2m+1}=q(B_{2m-1}+B_{2m+1})}$

關係式

馬丟方程的基本解${\displaystyle W_{I}W_{II}}$滿足下列關係：^[3]:

${\displaystyle {\begin{vmatrix}w_{I}(n,q,0)&w_{II}(n,q,0)\\w_{i}^{'}(n,q,0)&w_{II}^{'}(n,q,0)\end{vmatrix}}}$= ${\displaystyle {\begin{vmatrix}1&0\\0&1\end{vmatrix}}}$

郎斯基行列式： ${\displaystyle W[w_{I},w_{II}]=1}$

${\displaystyle w_{I}(a,q,z+\pi )=w_{I}(a,q,\pi )*w_{I}(a,q,z)+w_{I}^{'}(a,q,\pi )*w_{II}(a,q,z)}$ ${\displaystyle w_{I}(a,q,z-\pi )=w_{I}(a,q,\pi )*w_{I}(a,q,z)-w_{I}^{'}(a,q,\pi )*w_{II}(a,q,z)}$ ${\displaystyle w_{II}(a,q,z+\pi )=w_{II}(a,q,\pi )*w_{II}(a,q,z)+w_{II}^{'}(a,q,\pi )*w_{II}(a,q,z)}$ ${\displaystyle w_{II}(a,q,z-\pi )=w_{II}(a,q,\pi )*w_{II}(a,q,z)-w_{I}^{'}(a,q,\pi )*w_{II}(a,q,z)}$

${\displaystyle w_{I}(-z)=w_{I}(z)}$ ${\displaystyle w_{II}(-z)=-w_{II}(z)}$ ${\displaystyle }$ ${\displaystyle }$ ${\displaystyle }$ ${\displaystyle }$

特例

• ${\displaystyle CE(a,0,z)=cos(az)}$
• ${\displaystyle SE(a,0,z)=sin(az)}$
• ${\displaystyle MathieuA(1,0)=1}$
• ${\displaystyle MathieuA(a,0)=a^{2}}$
• ${\displaystyle MathieuB(a,0)=a^{2}}$
• ${\displaystyle MathieuFloquet(a,0,z)=exp(I*sqrt(a)*z)}$
• ${\displaystyle }$

夫洛開解

Mathieu Floquet

馬丟函數中，如果${\displaystyle f(x)}$ 是一個周期為${\displaystyle \omega }$的解，並滿足下列條件

${\displaystyle f(x+\omega )=\sigma *f(x)}$,其中${\displaystyle \sigma }$與x 無關，則此解稱為夫洛開解。

級數展開

${\displaystyle MF(1,1,z)={.7992-.5734*I+(-.9134+.6553*I)*z+(.3996-.2867*I)*z^{2}+(-.1523+.1092*I)*z^{3}+(-.2331+.1673*I)*z^{4}+O(z^{5})}}$ ${\displaystyle MF(1,2,z)={.7643-.4526*I+(-1.167+.6910*I)*z+(1.146-.6789*I)*z^{2}+(-.5835+.3455*I)*z^{3}+(-.2229+.1320*I)*z^{4}+O(z^{5})}}$ ${\displaystyle MF(1,3,z)={.6841-.3703*I+(-1.318+.7135*I)*z+(1.710-.9258*I)*z^{2}+(-1.098+.5946*I)*z^{3}+(0.2851e-1-0.1543e-1*I)*z^{4}+O(z^{5})}}$