热门问题
时间线
聊天
视角
三角不等式
来自维基百科,自由的百科全书
Remove ads
三角不等式是數學上的一個不等式,表示從A到B再到C的距離永不少於從A到C的距離;亦可以說是兩項獨立物件的量之和不少於其和的量。它除了適用於三角形之外,還適用於其他數學範疇及日常生活中。
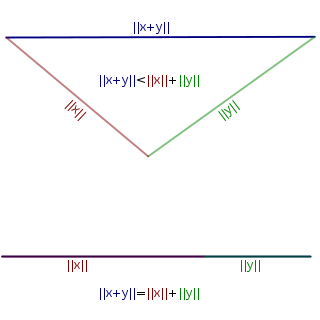
歐式几何
定理 —
任意三角形都有:
至於:
除非三點共線否則在欧氏几何中不可能,要有这种「三角形」只有在打破第五公設的非欧几里得几何裡才會出現,如球面幾何學的球面三角形。或閔考斯基時空:
- 对所有 ,使得, 和
Remove ads
向量空間
一種推廣三角不等式的方法是在「可相加和伸縮的空間」(向量空间)裡定義「長度」(范数),嚴格來說就是所謂的賦範向量空間。但三角不等式在賦範向量空間是個不能證明的前提,而且不一定具有幾何中:
的直觀性質,要確保這種直觀性質的話,需要退一步在向量空间假設内积的構造,換句話說有以下定理:
三角不等式 —
是個複內積空間,則對所有的 有:
(證明請見内积空间#三角不等式)
Remove ads
事實上,实数系跟複數系都是以自己為域(純量母空間)的向量空間,它們的向量加法就是普通的加法;純量積就是普通的乘法;至於內積的話,任二複數的內積可以定義成:
這樣範數就會等於绝对值:
而任二實數的內積就只是普通的乘法:
這樣兩系內的三角不等式都只是內積空間的特例:
定理 —
- ()
- ()
其實上面兩式也可以用更基礎,只牽涉到複數運算的方式證明:
Remove ads
維(实数)坐標空間本身就是以實數系為域(純量母空間)的向量空間,只要對任意和和純量 作如下定義:
(1)向量加法:
(2)純量乘法:
它也能成為實係數内积空间,只要作如下定義:
(3) 內積:
也就是普通的点积。這樣的話範數正好就等於直觀上的長度:
這樣實數座標空間的三角不等式就是內積空間不等式的特例了:
定理 —
- ()
如果把把歐幾里得平面和做一對一對應的話,歐式几何一節的三角不等式就可以視為上式的特例;但也可以使用空間座標的運算性質來證明:
定理 —
對坐标系中任三點有:
Remove ads
參見
参考文献
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads

















































 ,
,  ...
...















 ,
,  ...
...






