热门问题
时间线
聊天
视角
八維正九胞體
来自维基百科,自由的百科全书
Remove ads
在几何学中,八维正九胞体(enneazetton或ennea-8-tope)是一种自身对偶的正八维多胞体[1], 是八维空间的单纯形。八维正九胞体是八维空间中最简单的正图形,因此又称为8-单纯形(8-simplex)[2]。八维正九胞体由9个七维正八胞体的七维胞组成,其二面角为cos−1(1/8)约为82.82°[1]。乔纳森·鲍尔斯(Jonathan Bowers)将八维正九胞体缩写为ene[3]。
Remove ads
命名
八维正九胞体是一种八维单纯形,因此也称为8-单纯形,由于其具有9个七维胞,因此又称为九-七维胞体(英语:enneazetton)[4],其中,九(英语:ennea-)表示其有九个维面,七维胞(英语:zett-)表示其由七维胞体构成,然后加一个体(英语:-on)。[4]
性质
八维正九胞体共由9个顶点、36条边、84个三角形的面、126个正四面体的三维胞、126个正五胞体的四维胞、84个五维正六胞体的五维胞、36个六维正七胞体的六维胞和9个七维正八胞体的七维胞组成,其中七维正八胞体为八维正九胞体的维面。 若一个八维正九胞体的棱长为1,则其外接八维超球的半径为、内切八维超球的半径为。[1]
Remove ads
八维正九胞体可以看做是在八维空间中以七维正八胞体为底的锥体,即八维正九胞体可以透过将七维正八胞体置于八维空间中,并在正八胞体所在的七维空间外取一点,将七维正八胞体的每个顶点连结该点构成,因此八维正九胞体又称为八胞体八维锥(octaexal pyramid)。[1]
八维正九胞体是一个八维空间几何体,因此其体积为八维空间超体积,单位为八次方单位。边长为a的八维正九胞体,其超体积为:[1]
表面积是指将一个几何体表面维面的几何大小的和。在三维空间中,表面积为每个面之面积的总和。而八维正九胞体是一个八维空间几何体,因此其表面积为九个七维八胞体之超体积的和,单位为七次方单位。边长为a的八维正九胞体,其超表面积为:[1]
Remove ads
若一个八维正九胞体几何中心位于原点,且边长为2单位长,则其顶点坐标为:
在九维空间中,八维正九胞体的顶点坐标可以简化为(0,0,0,0,0,0,0,0,1)的全排列。这是因为八维正九胞体是九维正轴体的维面。[5]
Remove ads
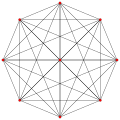
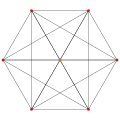
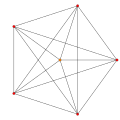
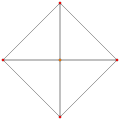
正交投影

参考文献
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads