割圜密率捷法

割圜密率捷法,清代数学家明安图积三十年之功写成；后子明新、弟子陳際新根据明安图遗稿整理、推究于乾隆三十九年（1774年）出版，时明安图已去世十年。^[1]

割圜密率捷法卷一

《割圜密率捷法》根据连比例三角形的性质，详细推导圆周率的九个无穷级数。中算史家李儼说“数与形的结合，堪与笛卡尔所创立的解析几何媲美”^[2]。

内容

卷一 步法

• 圆径求周

${\displaystyle 2*\pi *r={\frac {3*2*r}{4^{0}*1!}}+{\frac {1^{2}*3*2*r}{4^{1}*3!}}+{\frac {1^{2}*3^{2}*3*2*r}{4^{3}*5!}}+{\frac {1^{2}*3^{2}*5^{2}*7^{2}*9^{2}*11^{2}*13^{2}*15^{2}*17^{2}*19^{2}*3*2*r}{4^{1}0*21!}}}$+…………

可以改写成 ${\displaystyle {\frac {\pi }{3}}=\sum _{n=0}^{\infty }{\frac {((2n-1)!!)^{2}}{4^{n}*(2n+1)!}}}$^[3]。

此展开式被清代数学家称为“杜氏第一术”，出自牛顿。

• 弧背求正弦

杜氏九术之二，出自格列高里:^[4].

弧背为a,半径为r,通弦为c

${\displaystyle {\frac {c}{2}}=rsin(\alpha )=a-{\frac {a^{3}}{3!*r^{2}}}-{\frac {a^{5}}{5!*r^{4}}}+{\frac {a^{7}}{7!*r^{6}}}+}$……

• 弧背求正矢

“杜氏九术”之三，出自格列高里

${\displaystyle b=rvers\alpha ={\frac {a^{2}}{2!*r}}-{\frac {a^{4}}{4!*r^{3}}}+{\frac {a^{6}}{6!*r^{5}}}+}$…………

• 弧背求通弦

${\displaystyle 2*\pi *r=2*a-{\frac {(2a)^{3}}{4*3!*r^{2}}}+{\frac {(2*a)^{5}}{4^{2}*5!*r^{4}}}+{\frac {(2*a)^{7}}{4^{3}*7!*r^{6}}}}$+……

• 弧背求矢

${\displaystyle h={\frac {(2*a)^{2}}{4*2!*r}}-{\frac {(2*a)^{4}}{4^{2}*4!*r}}+{\frac {(2*a)^{6}}{4^{3}*6!*r}}}$+…………

• 通弦求弧背

出自明安图：

${\displaystyle 2a=\sum _{n=0}^{\infty }{\frac {[(2n-1)!!]^{2}*c^{2n+1}}{4^{n}*(2n+1)!*r^{2n}}}}$^[5]。

• 正弦求弧背

出自明安图

${\displaystyle a=\sum _{n=0}^{\infty }{\frac {[(2n-1)!!]^{2}*(r*sin\alpha )^{2n+1}}{(2n+1)!*r^{2n}}}}$^[6]。

• 正矢求弧背

${\displaystyle a^{2}=\sum _{n=0}^{\infty }{\frac {(n!)^{2}*(2b)^{n+1}}{(2n+2)!*r^{n-1}}}}$^[7]。

• 矢求弧背

${\displaystyle (2a)^{2}=\sum _{n=0}^{\infty }{\frac {2*(n!)^{2}*(8*r*vers\alpha )^{n+1}}{4^{n}*(2n+2)!*r^{n-1}}}}$^[8]。

• 余弧求正弦正矢

${\displaystyle rvers(90-\alpha )=rcvers(\alpha )}$

${\displaystyle r-rcovers(\alpha )=rsin(\alpha )}$

${\displaystyle rsin(90-\alpha )=rcos(\alpha )}$

${\displaystyle r-rcos(\alpha )=rvers(\alpha )}$

• 余矢余弦求本弧

  借弧背求正弦余弦

  借正弦余弦求弧背

卷二 用法

• 角度求八线
• 直线三角形边角相求
• 弧线三角形边角相求

卷三 法解上

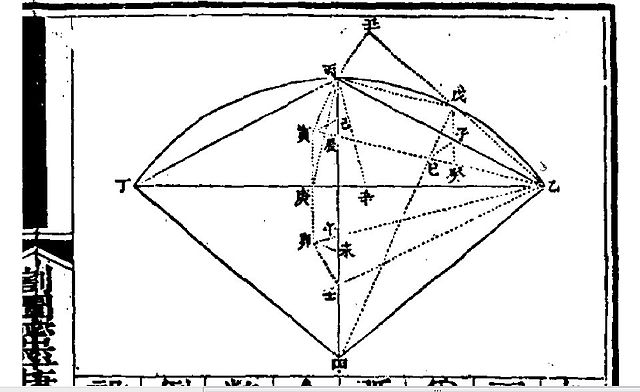分弧通弦率数求全弧通弦率图解

明安图镇此书中最先运用卡塔兰数

弧背求通弦图解

• 分弧通弦率数求全弧通弦率法解
• 弧背求通弦法解
• 通弦求弧背法解
• 弧背正弦相求法解

卷四 法解下

• 分弧正矢率数求全弧正矢率数法解
• 弧背求正矢法解
• 正矢求弧背法解
• 弧矢相求法解
• 弧矢弦正余互用法解
• 借弧背求正弦余弦法解
• 借正弦余弦求弧背法解