角平分线长公式

在平面几何中，角平分線長公式是計算三角形內、外角平分線長度的公式。在三角形 ${\displaystyle \triangle {ABC}}$ 中，${\displaystyle \angle A}$ 的内角平分線交对边 ${\displaystyle BC}$ 于点 ${\displaystyle D}$ ，外角平分線交直线 ${\displaystyle BC}$ 于点 ${\displaystyle E}$ ，则三角形的内、外角平分線的长度为：

${\displaystyle AD={\sqrt {AB\cdot AC-DB\cdot DC}}}$

${\displaystyle AE={\sqrt {EB\cdot EC-AB\cdot AC}}}$

三角形的内、外角平分线

若记 ${\displaystyle BC}$ 边长为 ${\displaystyle a}$ ，${\displaystyle AC}$ 边长为 ${\displaystyle b}$ ，${\displaystyle AB}$ 边长为 ${\displaystyle c}$ ，记内角平分線 ${\displaystyle AD}$ 长为 ${\displaystyle t_{a}}$ ，外角平分線 ${\displaystyle AE}$ 长为 ${\displaystyle t_{a}'}$ ，则三角形的内、外角平分線的长度可以表示为：

${\displaystyle t_{a}={\sqrt {bc(1-{a^{2} \over (b+c)^{2}})}}}$ ${\displaystyle ={bc \over b+c}{\sqrt {2+2\cos A}}}$ ${\displaystyle ={2bc \over b+c}\cdot \cos {A \over 2}}$

${\displaystyle t_{a}'={\sqrt {bc({a^{2} \over (b-c)^{2}}-1)}}}$ ${\displaystyle ={bc \over |b-c|}{\sqrt {2-2\cos A}}}$ ${\displaystyle ={2bc \over |b-c|}\cdot \sin {A \over 2}}$

证明

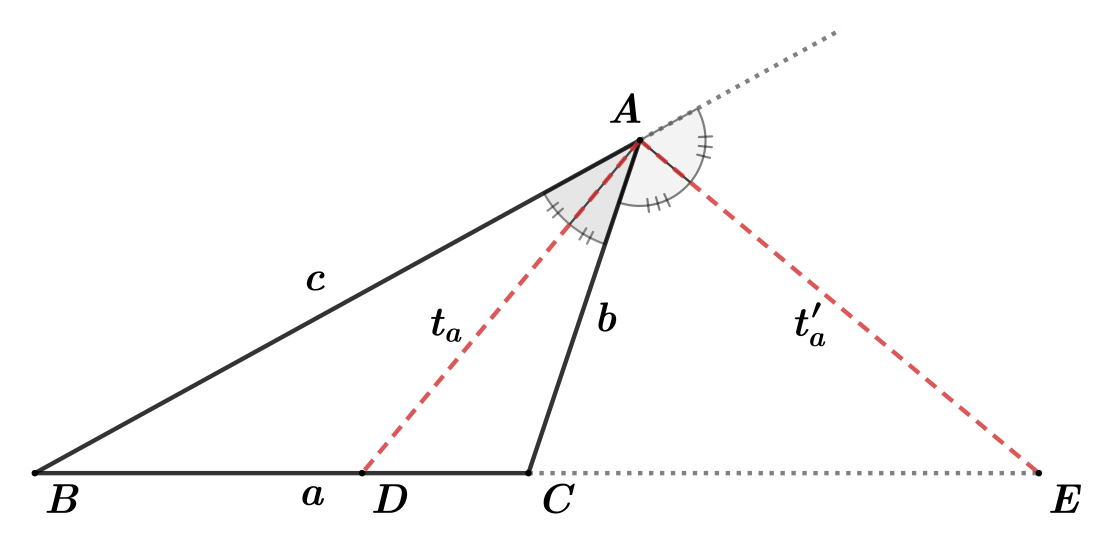
三角形ABC以及關於角A的平分線

内角平分线长

作 ${\displaystyle \angle A}$ 的内角平分線交对边 ${\displaystyle BC}$ 于点 ${\displaystyle D}$ 。延长 ${\displaystyle {\overline {AD}}}$ 至点 ${\displaystyle E}$ ，使 ${\displaystyle \angle AEB=\angle ACD}$ 。

${\displaystyle \triangle AEB\sim \triangle ACD\Rightarrow AE\cdot AD=AB\cdot AC}$

${\displaystyle \triangle DEB\sim \triangle DCA\Rightarrow DE\cdot AD=BD\cdot DC}$

${\displaystyle AD^{2}=(AE-DE)\cdot AD=AE\cdot AD-DE\cdot AD=AB\cdot AC-DB\cdot DC}$

得内角平分线长公式（i）：^[1][2][3]

${\displaystyle AD={\sqrt {AB\cdot AC-DB\cdot DC}}}$

外角平分线长

作 ${\displaystyle \angle A}$ 的外角平分線交直线 ${\displaystyle BC}$ 于点 ${\displaystyle D'}$ 。延长 ${\displaystyle {\overline {D'A}}}$ 至点 ${\displaystyle E'}$ ，使 ${\displaystyle \angle AE'B=\angle ACD'}$ 。

${\displaystyle \triangle AE'B\sim \triangle ACD'\Rightarrow AE'\cdot AD'=AB\cdot AC}$

${\displaystyle \triangle D'E'B\sim \triangle D'CA\Rightarrow D'E'\cdot AD'=BD'\cdot D'C}$

${\displaystyle AD'^{2}=(D'E'-AE')\cdot AD'=D'E'\cdot AD'-AE'\cdot AD'=D'B\cdot D'C-AB\cdot AC}$

得外角平分线长公式（i）：^[2]

${\displaystyle AD'={\sqrt {D'B\cdot D'C-AB\cdot AC}}}$

推导

根据角平分线定理，有：^[4]

${\displaystyle DB={ac \over b+c},\ DC={ab \over b+c}}$

${\displaystyle D'B={ac \over |b-c|},\ D'C={ab \over |b-c|}}$

代入式（i），得到角平分线长公式（ii）：^[5][3]

${\displaystyle t_{a}={\sqrt {bc(1-{a^{2} \over (b+c)^{2}})}}}$

${\displaystyle t_{a}'={\sqrt {bc({a^{2} \over (b-c)^{2}}-1)}}}$

将余弦公式代入式（ii），得到角平分线长公式（iii）：

${\displaystyle t_{a}={bc \over b+c}{\sqrt {2+2\cos A}}}$

${\displaystyle t_{a}'={bc \over |b-c|}{\sqrt {2-2\cos A}}}$

将半角公式代入式（iii），得到角平分线长公式（iv）：^[6]

${\displaystyle t_{a}={2bc \over b+c}\cdot \cos {A \over 2}}$

${\displaystyle t_{a}'={2bc \over |b-c|}\cdot \sin {A \over 2}}$

与其他定理的关系

斯图尔特定理

角平分线长公式是斯图尔特定理的特殊情况，或者说推论。根据斯图尔特定理，对于三角形 ${\displaystyle \triangle {ABC}}$ 的任意一边 ${\displaystyle BC}$ 上的任意一点 ${\displaystyle D}$ ，有：

${\displaystyle AD^{2}=AB^{2}\cdot {DC \over BC}+AC^{2}\cdot {DB \over BC}-DB\cdot DC}$

当点 ${\displaystyle D}$ 是内角平分线足时，根据角平分线定理，有：

${\displaystyle {AB \over DB}={AC \over DC}={AB+AC \over BC}}$

联立之后，即可得到内角平分线长公式（i）或（ii）。同理，可以推出外角平分线长公式（i）或（ii）。^[5][2]

施泰纳-莱穆斯定理

利用角平分線長公式，可以证明施泰纳-莱穆斯定理——有两条内角平分线长度相等的三角形是等腰三角形。^[7]

${\displaystyle t_{a}=t_{b}\ \,\Rightarrow \ \,{\sqrt {bc(1-{a^{2} \over (b+c)^{2}})}}={\sqrt {ac(1-{b^{2} \over (a+c)^{2}})}}}$

化简后得到： ${\displaystyle c(a+b+c)(a-b)[(a+b)(c^{2}+ab)+3abc+c^{3}]=0}$

连乘的其他各项都为正数，从而推出： ${\displaystyle a-b=0}$

名称

在欧美，角平分線長公式没有特殊的名称。^[5][2][7]在中国大陆，有文獻將内角平分線長公式（i）称为“斯库顿定理”，乃是以荷兰数学家弗兰斯·范斯霍滕（英语：Frans van Schooten）命名。^[1][8][9]而在欧美，范斯霍滕定理（英语：Van Schooten's theorem）指的是等边三角形外接圆的一个性质，与三角形角平分线无关。^[10]

參見

• 中線長公式
• 角平分線定理

参考文献

1. 孙建斌. Schooten定理的证明. 数学教学研究. 1986, (1): 3-6.
2. 别列标尔金（俄语：Перепёлкин, Дмитрий Иванович）. 初等几何学教程 上卷. 马忠林 (译). 北京: 高等教育出版社. 1955: 202-204.
3. Amarasinghe, G. W. I. S. On the standard lengths of angle bisectors and the angle bisector theorem (PDF). Global Journal of Advanced Research on Classical and Modern Geometries. 2012, 1 (1): 15-27 [2023-06-24]. （原始内容存档 (PDF)于2022-06-18） （英语）.
4. Heath, Thomas L. The Thirteen Books of Euclid's Elements (PDF) II. Cambridge: Cambridge University Press. 1908: 197 [2023-06-24]. （原始内容存档 (PDF)于2022-02-02） （英语）.
5. Hadamard, Jacques. Leçons de géométrie élémentaire (géométrie plane). Paris: Armand Colin et Cie. 1898: 122-125 （法语）.
6. The angle bisector. Formula 2. mathvox.com. [2023-06-24]. （原始内容存档于2023-06-17） （英语）.
7. Trigg, Charles W. Mathematical Quickies. New York: Dover Publications. 1985: 103 [1967]. ISBN 0-486-24949-2 （英语）.
8. 刘运谊. 斯库顿定理及其应用. 数学教学通讯. 1994, (6): 12+39.
9. 黄家礼. 几何明珠. 北京: 科学普及出版社. 1997: 78. ISBN 7-110-03511-5.
10. Raymond, Viglione. Proof Without Words: van Schooten's Theorem. Mathematics Magazine. 2016, 89 (2): 132 （英语）.