變換幾何

在数学领域，变换几何（英語：Transformation geometry）是一种通过聚焦于几何变换群及在其作用下保持不变的性质来研究几何学的教学方法。这种理念不同于以证明几何定理为核心的欧几里得几何经典法。

例如，在变换几何的框架下，等腰三角形的性质可以通过"其能够沿某条对称轴反射映射的图形与自身重合"这一事实推导得出。这与古典几何中通过三角形全等准则进行证明的方式形成鲜明对比^[1]。

将变换作为几何学基础的第一个系统性的探索由费利克斯·克莱因于19世纪提出，即著名的埃尔朗根纲领。约一个世纪内，该方法主要局限于数学领域。直至20世纪，教育界开始尝试将其运用于教学领域：安德烈·柯尔莫哥洛夫在推动俄罗斯几何教学方案改革时，将此方法（与集合论共同）纳入为核心内容^[2]。这些探索在1960年代伴随名为"新数学运动"的数学教育整体改革达到高潮。

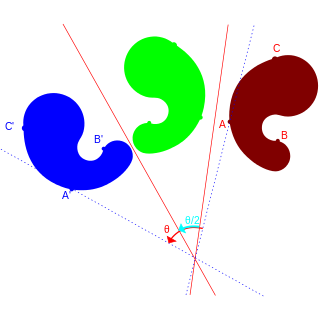
对变换几何的探索一般始于对日常生活中反射对称现象的研究。最初的变换是直线反射（即关于轴的反射）。两个反射的复合会产生旋转（当两直线相交时）或平移（当两直线平行时）。学生可以通过这类变换理解欧几里得平面的等距变换。例如，考察关于垂直线和与水平线成45°夹角直线的复合反射：正向复合会产生逆时针旋转90°，而逆向复合则会产生顺时针旋转90°。这类结果说明变换几何包含非交换过程。

直线反射的一个应用体现在对"任意三角形中的七分之一面积三角形"的几何证明中。

向低龄学生引入的另一类变换是放缩变换。不过圆的反演变换因其复杂性通常不适合低年级教学，因此更广泛的反演几何研究一般安排在大学阶段。

变换几何对具体对称群的实验可以为抽象群论的学习奠定基础。而其他实践活动则通过复数、超复数或矩阵运算来呈现几何的变换。这种教学视角与古典几何形成鲜明对比，当学生后续接触解析几何时，坐标旋转与反射的概念便能快速衔接。所有这些概念都为线性代数中反射概念的拓展做好了准备。

教育工作者们已对其展现出了相当兴趣，并且设计了从幼儿园到高中各学段的变换几何教学方案。针对低龄儿童，为避免引入专业术语并关联其日常经验，建议使用"翻转"指代直线反射，"平移"指代位移，"旋转"指代转动尽管这些并非精确的数学语言。部分方案要求学生先操作实体模型，再通过点集映射定义理解抽象的变换^[3]^[4]^[5]。

在推动改革俄罗斯的几何课程时，柯尔莫哥洛夫主张从变换视角重构课程体系，使几何教学建立在集合论基础上。这导致"全等"取代了传统的"相等"表述：由于图形被视为点集，它只能与自身相等，而通过等距变换能完全重合的两个三角形则被称为全等^[2]。

有位作者如此讲述群论对变换几何的重要性："我刻意从基本原理出发构建了所需的群论体系，意在能使本书作为变换群及抽象群论概念的启蒙读本，即使你从未接触过这些领域"。^[6]

在教学领域的应用

参见

参考资料

延伸阅读

Wikiwand - on