範疇論(英語:Category theory)是數學的一門學科,是關於數學結構及其關係的一般理論,以抽象的方法處理數學概念,將這些概念形式化成一組組的「物件」及「態射」。數學中許多重要的領域可以形式化為範疇。使用範疇論可以令這些領域中許多難理解、難捉摸的數學結論更容易敘述證明。
此條目需要補充更多來源。 (2022年10月9日) |

一個範疇包含兩類數學物件:物件與態射。以集合範疇為例,其物件為集合,態射為集合間的函數。若以第一個態射的目標為源發出第二個態射,這樣形成的「複合態射」的性質同複合函數類似(存在結合律與單位態射)。但需注意,範疇的物件不一定要是集合,態射也不一定要是函數;一個數學概念若可以找到一種方法,以符合物件及態射的定義,則可形成一個有效的範疇,且所有在範疇論中導出的結論都可應用在這個數學概念之上。
範疇最簡單的例子之一為廣群,其態射皆為可逆的。群胚的概念在拓撲學中很重要。範疇現在在大部分的數學分支中都有出現,在理論電腦科學的某些領域中用於對應資料型別,而在數學物理中被用來描述向量空間。
範疇論不只是對研究範疇論的人有意義,對其他數學家而言也有着其他的意思。一個可追溯至1940年代的述語「一般化的抽象廢話」,即被用來指範疇論那相對於其他傳統的數學分支更高階的抽象化。
背景
研究範疇就是試圖以「公理化」的方法抓住在各種相關連的「數學結構」中的共同特性,並以結構間的「結構保持函數」將這些結構相關起來。因此,對範疇論系統化的研究將允許任何一個此類數學結構的普遍結論由範疇的公理中證出。
考慮下面的例子:由群組成的類Grp包含了所有具有「群結構」的物件。要證明有關群的定理,即可由此套公理進行邏輯的推導。例如,由公理中可立即證明出,群的單位元素是唯一的。
不是只專注在有特定結構的個別物件(如群)上,範疇論會着重在這些物件的態射(結構保持映射)上;經由研究這些態射,可以學到更多關於這些物件的結構。以群為例,其態射為群同態。兩個群間的群同態會嚴格地「保持群的結構」,這是個以將一個群中有關結構的訊息運到另一個群的方法,使這個群可以看做是另一個群的「過程」。因此,對群同態的研究提供了一個得以研究群的普遍特性及群公理的推論的工具。
類似的研究也出現在其他許多的數學理論中,如在拓撲學中對拓撲空間的連續映射的研究(相關範疇稱為Top),及對流形的光滑函數的研究等。
再抽象化一次,範疇自身亦為數學結構的一種,因此可以尋找在某一意義下會保持其結構的「過程」;此一過程即稱之為函子。函子將一個範疇的每個物件和另一個範疇的物件相關連起來,並將第一個範疇的每個態射和第二個範疇的態射相關連起來。
實際上,即是定義了一個「範疇和函子」的範疇,其元件為範疇,(範疇間的)態射為函子。
經由研究範疇和函子,不只是學習了一類數學結構,及在其之間的態射;還學習了「在不同類型的數學結構之間的關係」。此一基本概念首次出現於代數拓撲之中。不同的「拓撲」問題可以轉換至通常較易解答的「代數」問題之上。在拓撲空間上如基本群或基本群胚等基本的架構,可以表示成由群胚所組成的範疇之間的基本函子,而這個概念在代數及其應用之中是很普遍的。
再抽象化一次,架構通常會「自然地相關連」,這個第一眼會覺得很曖昧的概念,產生了自然變換(將一個函子映射至另一函子的方法)此一清楚的概念。許多數學上的重要架構可以從此一角度來研究。
歷史註記
範疇、函子和自然轉換是由塞繆爾·艾倫伯格和桑德斯·麥克蘭恩在1945年引進的。這些概念最初出現在拓撲學,尤其是代數拓撲學里,在同態(具有幾何直觀)轉化成同調論(公理化方法)的過程中起了重要作用。烏拉姆說,在1930年代的後期,波蘭學派中曾出現類似的想法。
艾倫堡和麥克蘭說,他們的目的在於理解自然映射;為此,必須定義函子;為了定義函子,就自然地要引進範疇。
同調代數由於計算上的需要而使用範疇論,這對範疇論起到了推進作用;此後範疇論又在代數幾何的公理化過程中得到發展。代數幾何與羅素-懷特海德的關於數學統一性基礎的觀點相牴觸。廣義範疇論隨後產生,且更容納了語意靈活性和高階邏輯等多種新特徵的泛代數,現在被運用到數學的所有分支。
特殊範疇拓撲斯甚至可以代替公理集合論作為數學的基礎。然而範疇論對這些範圍廣泛的基礎應用還是有爭議的;但作為構造性數學的基礎或註釋,範疇論被研究的相當透徹。儘管如此,公理集合論至今仍然是數學家們的通用語言,並沒有被範疇論的註釋所取代。將範疇論引入大學程度的教學(在《伯克霍夫-麥克蘭》和《麥克蘭-伯克霍夫》這兩本抽象代數的教科書的區別上可以印證)還是遭到了相當的反對。
範疇邏輯是直覺邏輯中類型論的一個被明確定義的分支,在計算機學科的函數式編程和體理論中均有應用,並且都是在笛卡爾閉範疇中對λ演算的非句法性描述。至少,用範疇論可以精確地描述在這些相關的領域里什麼是共同的(在抽象的意義上)。
範疇、物件與態射
一個「範疇」 由如下3個數學物件組成:
- 一個類 ,其元素稱為「物件」;
- 一個類 ,其元素稱為「態射」或「箭號」。每個態射 都只有一個「源物件」 及一個「目標物件」 (其中 和 都在 內),稱之為「從 至 的態射」,標記為 。
所有從 至 的態射所組成的類稱之為「態射類」,標記為 、 或 。 - 一個二元運算,稱為「態射複合」,使得對任意三個物件 、 及 ,都會有 。兩個態射 及 的複合寫做 或 [註 1],並會符合下列兩個公理:
由以上公理可證得,每個物件都只存在一個單位態射。有些作者將物件本身用單位態射來定義,這在本質上是相同的。
如果物件的類確實是個集合,那麼這種範疇就被稱為「小範疇」。許多重要的範疇不是小範疇。
範疇中的態射有時又稱為「箭號」,這種叫法來自於交換圖。
每一範疇都由其物件,態射,和複合態射來表述。為了方便起見,以下的「函數」即是指態射,不再一一說明。
- Set 是所有集合和它們彼此之間的全函數構成的範疇
- Ord 是所有預序集和其間的單調函數構成的範疇
- Mag 是所有廣群和其間的同態映射構成的範疇
- Med 是所有對換廣群和其間的同態映射構成的範疇
- Grp 是所有群和其間的群同態構成的範疇
- Ab 是所有阿貝爾群和其間的群同態構成的範疇
- VectK 是所有體 (固定)上的向量空間和其間的線性映射構成的範疇
- Top 是所有拓撲空間和其間的連續函數構成的範疇
- Met 是所有度量空間和其間的測地映射構成的範疇
- Uni 是所有均勻空間和其間的均勻連續函數構成的範疇
- 任何偏序集構成一個小範疇,其物件是的元素,其態射是從指向的箭頭,其中。
- 任何以單一物件(為任意固定集合)為基礎的獨異點構成一個小範疇。獨異點的任意元素通過二元運算給出一個從到的映射,所有這些映射恰好是範疇的所有態射;範疇的複合態射也正好是獨異點的二元運算。事實上,範疇可以看成獨異點的推廣;關於獨異點的定義和定理有一些可以推廣到範疇。
- 任何有向圖對應於一個小範疇:其物件是圖的頂點,其態射是圖的路徑,其複合態射是路徑的連接。稱此範疇為有向圖的「自由範疇」。
- 設是個集合,「上的離散範疇」是一個小範疇,以的元素為物件,以的恆等映射為其唯一的態射。
- 任何範疇可以在另一種看法下成為一個新的範疇:它具有相同的物件,然而所有態射都是反方向的。稱此為「對偶」或者「反範疇」,記作 (來自英文的opposite,意為「相反」)。
- 設和是範疇,則它們的「直積範疇」被定義為:其物件為取自的一個物件和取自的一個物件的有序對,其態射亦為取自的一個態射和取自的一個態射的有序對,其複合態射則由其分量分別複合。
映射之間的關係(比如)在大多數情形下可用更直觀的交換圖來表示,在此圖中物件被表示成頂點,態射被表示為箭頭。
一個表為的態射可具有以下任意一種性質。
- 自同構:若即同構,也自同態。表示的自同構類。
- 屈態射(retraction):若的右逆存在。即有態射和。
- 切態射(section):若的左逆存在。即有態射和。
屈態射必為滿態射,切態射必為單態射。另外,下面三條表述等價:
- 是單態射,也是屈態射;
- 是滿態射,也是切態射;
- 同構。
函子
函子是範疇之間保持結構的映射,可以看成以所有(小)範疇為成員的範疇中的態射。
一個從範疇到範疇的(協變)函子被定義為:
- 對中任意物件,都有一個中相應的物件與其對應;
- 對中任意態射 ,都有一個中相應的態射與其對應;
並使下列性質成立:
- 對中任意物件,都有。
- 對中任意兩個態射和,都有 。
一個從範疇到範疇的反變函子不同於函子的地方僅在於將中的映射箭頭倒過來。比如說是中任一態射,則有。定義反變函子的最簡捷的方法是作為的反範疇到上的函子。
有關函子的具體例子和性質請詳見函子條目。
自然和自然同構
「自然轉換」是兩個函子之間的關係。函子通常用來描述「自然構造」,而自然轉換則描述函子間的「自然同態」。有時,兩個截然不同的構造會產生「相同」結果,這可以用函子之間的自然同態來表述。
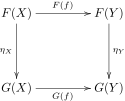
如果和是從範疇到範疇的(協變)函子,則從到的一個自然轉換會給中的每個物件,關聯一個中相應的態射,使得對中的任何態射,都有;這也就是說下列圖表是可交換的:
如有從到的自然轉換,使得對中所有物件來說都同構,則稱這兩個函子和「自然同構」。
設是體,是上的任意向量空間,則有從向量空間到其二重對偶的一個「自然」內射型線性映射 。這些映射在以下意義上是「自然」的:二重對偶運算是一個函子,這些映射正好構成了從恆等函子到二重對偶函子的自然轉換。如果向量空間的維數是有限的,我們就得到一個自然同構;因為「有限向量空間自然同構於其二重對偶」。
考慮阿貝爾群及其同態構成的範疇。對任意阿貝爾群、和,我們得到群同構
- 。
這些同構是「自然」的,因為它們定義了兩個函子間的一種自然轉換:。
泛結構、極限和上極限
運用範疇論的語言,許多數學研究領域都可以歸結成一些恰當的範疇,例如所有集合的範疇,所有群的範疇,所有拓撲的範疇,等等。這些範疇里的確有一些「特殊的」物件,例如空集或者兩個拓撲的直積。然而,在範疇的定義里,物件是原子性的,那就是說,我們無法知道一個物件到底是集合,是拓撲,還是其它抽象概念。有必要定義特殊物件而不涉及物件的內在結構,這是一個挑戰。那麼到底怎樣不用元素而定義空集,不用開集而定義拓撲積呢?
解決這個問題的途徑是借用物件和物件之間的關係,而這些關係由相應範疇中的態射給出。現在問題轉化為尋找泛性質,這些泛性質可以唯一地決定我們所感興趣的物件。事實上,為數眾多的重要結構都可用純範疇論的方法來描述。在定義泛性質時,我們要用到一個非常關鍵的概念:範疇性「極限」和其「上極限」。
等價範疇
人們很自然地要問,在什麼樣的情形下,兩個範疇「在本質上是相同」的,換一句話來說,對其中一個範疇成立的定理,可以既定地轉換成另一個範疇的定理。用來描述這種情形的主要方法是「範疇的等價性」,由函子給出。範疇的等價性在數學中有很多的應用。
進一步的概念和結果
範疇和函子的定義只是範疇代數中最基本的部分。除此之外的重要部分如下列所述。基本上是以閱讀順序排列,儘管它們彼此之間有着內在的聯繫。
高維範疇
上述許多概念,特別是範疇的等價性、伴隨函子和函子範疇等,可抽象至更高維的背景中。簡而言之,若將態射視為「從一個物件到另一個物件的過程」,那麼高維範疇就允許我們考慮「高維過程」,從而方便地概括之。
例如,(嚴格)2-範疇是與「態射間的態射」一起的範疇,即允許態射轉換的過程。然後便可以對這些「雙態射」進行橫縱向的「組合」,通過規定二維的「交換律」,聯繫起兩個合成律。這方面的標準例子是Cat,即所有(小)範疇的二維範疇,其中態射的雙態射僅僅是通常意義上的態射的自然轉換。另一個基本例子是,考慮一個具有單一物件的二維範疇,即么半範疇。雙範疇是比二維範疇弱的概念。其中態射的組成不是嚴格意義上的關聯,而只是平凡的同構。
這個過程可以擴展到任意自然數維,稱為n維範疇。甚至還有與序數ω對應的ω維範疇的概念。
高維範疇是更廣泛的高維代數的一部分。
範疇分類
- 在許多範疇中,態射集合不僅僅是集合,實際上是阿貝爾群,態射的複合具有群結構,也就是說是雙線性的。這種範疇被稱為預加性的。如果這種範疇還具有所有有限的積和上積,則稱為加性範疇。如果所有具有一個核和一個上核,那麼所有滿射都是上核,所有單射都是核,我們稱此為阿貝爾範疇。阿貝爾範疇的一個典型的例子是阿貝爾群所組成的範疇。
- 一個範疇被稱為是完備的,如果所有極限存在。集合,阿貝爾群和拓撲空間的範疇是完備的。
- 一個範疇被稱為是笛卡兒閉性的,如果它具有有限直積,並且一個定義在有限乘積上的態射總是可以表示成定義在其中一個因子上的態射。
- 一個拓撲斯是一種特殊的笛卡兒閉範疇,在其中可表述(公理化)所有的數學結構(就象傳統上使用集合論可以表示所有數學結構)。一個拓撲斯也可以用來表述一個邏輯理論。
- 一個群胚是這樣一種範疇,其中每一個映射都是一個同構。群胚是群、群作用和等價關係的推廣。
研究史
| 「 | 首先應注意到,整個範疇的概念基本上是個輔助性的概念;我們的基本概念,基本上就是函子和自然轉換[...] | 」 |
| ——Eilenberg和Mac Lane (1945) [1] | ||
雖然塞繆爾·艾倫伯格和桑德斯·麥克萊恩在1942年一篇關於群論的論文中已經給出了函子和自然轉換的具體例子,[2]他們在1945年的一篇論文中,向這些概念引入了更普遍的意義,還有範疇的額外概念[1],並討論了範疇論在代數拓撲領域的應用。[3]這些工作是直觀幾何同調到同調代數過渡的一個重要部分。
以斯塔尼斯拉夫·烏拉姆名義寫的一系列文章,都聲稱類似的想法在1930年代末的波蘭已經流行了。艾倫伯格是波蘭人,1930年代在波蘭學習數學。範疇論在某種意義上也是埃米·諾特將抽象過程形式化的延續;[4]諾特意識到,理解一種數學結構需要理解保留了結構的過程(同構)。[來源請求]艾倫伯格和麥克萊恩引入了範疇,用於理解和形式化將代數結構(拓撲不變量)與拓撲學結構相關聯的過程(函子)。
範疇論最初源自同調代數的需要,並為現代代數幾何(概形論)的需要而得到廣泛擴展。範疇論可被視為泛代數的延伸,後者研究代數結構,前者則適用於任何數學結構,並研究不同性質的結構間的關係,因此可用於整個數學領域。在數理邏輯和語義(範疇抽象機)上的應用來得較晚。
某些稱作拓撲斯(topos,單數topoi)的範疇甚至可以替代公理集合論作為數學的基礎。拓撲斯也可看做是特定類型的範疇,有兩個額外的拓撲斯公理。範疇論的這些基礎應用已經研究得相當詳細,常是作為數學構成主義的基礎。拓撲斯理論是抽象層論的一種形式,源於幾何學,啟發了諸如無點拓撲學之類想法。
範疇邏輯現在是基於直覺主義邏輯類型論,定義明確的領域,並在函數式編程和體理論中得到應用,其中一個笛卡兒閉範疇被視作λ演算的非語義描述。範疇論澄清了領域間在某種抽象意義上的共同點。
範疇論還有其他應用。例如,約翰·拜艾茲展示了物理學中費曼圖和么半範疇之間的聯繫。[5]範疇論的另一個應用是拓撲斯理論,已在數學音樂理論中得到了應用,可參Guerino Mazzola的書《音樂的拓撲斯,概念、理論和表現的集合邏輯》。
註釋
參考資料
延伸閱讀
外部連結
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.