Matematikkens historie
From Wikipedia, the free encyclopedia
Matematikkens historie går flere tusen år tilbake i tid, lenge før ordet matematikk oppstod. Ordet «matematikk» kommer fra gresk μάθημα (máthema) som betyr vitenskap, kunnskap eller læring, og μαθηματικός (mathematikós) betyr «glad i å lære».[1] I dag gjelder begrepet en bestemt kunnskapsgren – et deduktivt studium av antall, struktur, rom og endring.

Lenge før matematikk utviklet seg som eget kunnskapsområde har menneskene vært opptatt av antall, strukturer, former og figurer, lokalisering i rommet og andre emner knyttet til matematikk. Den mest fundamentale matematiske prosessen er telling,[2] så det er naturlig å starte matematikkens historie med tall og tallsystemer. Tidlig ble det også behov for å kunne måle og veie, og å kunne sammenligne ulike størrelser. Fra primitiv telling og måling har matematikk gradvis utviklet seg til mer og mer generelle og abstrakte idéer og teorier.
De eldste matematiske tekstene vi kjenner stammer fra det gamle Mesopotamia, fra omkring 1800 f.Kr., og fra det gamle Egypt, fra omkring 1650 f.Kr. Også i India har man funnet gamle matematiske tekster, fra mellom 800 og 500 f.Kr. De eldste tekstene omtaler problemstillinger og metoder i aritmetikk og geometri, og i alle tre landområdene har en hatt kjennskap til det som i dag omtales som Pytagoras’ læresetning. Fra Kina kjenner vi svært gamle matematiske tekster.
Grunnen for matematikk som eget fagområde ble lagt i antikkens Hellas. I det 6. århundre før Kristus blandet Pytagoras og hans disipler matematikk, musikk og mystisisme, i en skole der kunnskap om tall og geometri sto sentralt. Euklid levde i Alexandria omkring 300 før Kristus, og Euklids Elementer ble med sin aksiomatiske tilnærmingsmåte en viktig lærebok i flere tusen år. Også Arkimedes (født ca 287 f.Kr.) skulle få stor betydning for senere vitenskap i middelalderen. Kunnskap om gresk matematikk ble for en stor del glemt i Europa, men ble tatt vare på og videreutviklet i den muslimske verden, i Arabia og Persia. I middelalderen ble arabiske tekster oversatt til latin, og disse oversettelsene formidlet kunnskap om både gresk, arabisk og indisk matematikk til Europa. Ikke minst viktig var introduksjonen av de hindu-arabiske tallene til Europa, på 1200-tallet.
Utviklingen av matematikk i europeisk middelalder var langsom, men ble stimulert ved opprettingen av de første universitetene. Mens grekerne i antikken i hovedsak unngikk uendelige prosesser, studerte europeiske matematikere på 1400-tallet uendelige følger og rekker. Drevet fram av behov innenfor navigasjon ble trigonometri en stadig viktigere del av matematikk. François Viète (1540–1603) innførte bruk av bokstaver i ligninger og la på den måten grunnlaget for moderne matematisk notasjon.
Matematikk har alltid vært et viktig verktøy i naturvitenskapene, og framskritt i matematikk har nesten alltid gått parallelt med utvikling i andre fag, ikke minst i fysikk og astronomi. Mange naturvitenskapsmenn, som Galileo Galilei (1564–1642) og Johannes Kepler (1571–1630), bidro også til utviklingen av matematikk.
Sentralt i utviklingen på 1700-tallet sto innføringen av analytisk geometri av René Descartes (1596–1650) og Pierre de Fermat (1607–1665). En milepæl var også etableringen av differensial- og integralregning, der grunnlaget ble lagt av Gottfried Leibniz (1646–1716) og Isaac Newton (1642–1726). Funksjonsbegrepet vokste fram fra studiet av geometriske kurver og ligninger. En gradvis standardisering av matematisk notasjon ble nå etablert, ikke minst påvirket av arbeidene til Leibniz og Leonhard Euler (1707–1783).
Studiet av algebraiske ligninger hadde på 1600-tallet ført til innføring av komplekse tall, et viktig steg i en prosess der matematiske størrelser ble mer og mer abstrakte. Bruken av denne formen for tall tok for alvor fatt med arbeidene til Leonhard Euler og med etablering av kompleks funksjonsanalyse, av Augustin Louis Cauchy (1789–1857). Carl Friedrich Gauss (1777–1855), kanskje den største matematikeren noensinne, beviste blant annet fundamentalteoremet i algebra, om eksistensen av komplekse røtter i en polynomligning.
Oppdagelsen av at det er mulig å definere ikke-euklidske geometrier fikk mange til å se på grunnlaget for matematikk med nye øyne. Også utforskning av patologiske funksjoner viste at mange intuitive begrep trengte en tydeligere klargjøring. På 1800- og 1900-tallet arbeidet mange matematikere med å etablere et stringent grunnlag for matematikken. Karl Weierstrass (1815–1897) var sentral i prosessen med å klargjøre skillet mellom geometri og algebra, i en prosess som i ettertiden er kalt «aritmetrisering av analysen». Mengdelæren, innført av Georg Cantor (1845–1918), la grunnlaget for en ny uttrykksmåte, som i dag brukes i nær sagt alle deler av matematikk. Studiet av matematiske strukturer, som grupper, metriske rom og vektorrom, var viktig for utviklingen av abstrakt algebra.
David Hilbert (1862–1943) formulerte i 1900 en liste på 23 uløste matematiske problem, en liste som fikk stor innflytelse på utviklingen i nyere matematikk. En av utfordringene var å bevise at aritmetikkens aksiomer er konsistente. Idealbildet av et fullkomment matematisk system fikk imidlertid flere skudd for baugen på 1900-tallet, ikke minst da Kurt Gödel (1906–1978) viste at det ikke er mulig å definere et formelt aksiomatisk system som grunnlag for hele matematikken.
I nyere tid har det oppstått mange nye retninger i matematikk, for eksempel numerisk analyse, stimulert av utviklingen av datamaskiner. Matematikken fortsetter å utvikle seg både i bredden og dybden, og faget er i dag så omfattende at det er umulig for en matematiker å ha oversikt over alt.
Forhistorisk tid, antikken og middelalderen

Forhistorisk matematikk
Opphavet til matematikk ligger i menneskets behov for å kunne telle, å kunne måle og å kunne beskrive størrelse og form. Alt i tidlige samler- og jeger-samfunn har det vært viktig å kunne formidle antall, for eksempel antall dyr og antall fiender. Strukturen i flere språk kan indikere at de første former for primitiv telling har vært basert på et skille mellom «en», «to» og «mange». Innsikten om at to steiner og to fisk har noe felles, representerer en første form for abstraksjon som er fundamental i matematikk.
Naturlig nok har kroppen lenge vært brukt som hjelpemiddel, og alt Aristoteles bemerket at telling basert på fem og ti er en direkte konsekvens av antall fingrer og tær.[3] Det engelske ordet «digit» for tall har opphav i det latinske «digitus», som betyr «finger».[4] Også mange navn på primitive måleenheter viser opphav i kroppen, for eksempel knyttet til hånd-, fot- og armlengde.
Ved arkeologiske utgravninger i Tsjekkoslovakia er det gjort funn av et lårben fra en ulv som er datert til omkring 30 000 f.Kr.[5] På dette benet er det risset inn 55 streker, systematisk etter hverandre. I Sentral-Afrika ble det i 1960 funnet et leggben av en ape, også dette med innrissede streker delt inn i grupper. Dette såkalte Ishango-benet er tidfestet til mellom 20 000 f.Kr. og 18 000 f.Kr., og strekene er blitt tolket som en form for telling eller en kalender.[trenger referanse]
Primitiv telling har vært basert på å risse inn streker og kanskje også ved å sammenligne med et antall pinner, steiner og lignende. En nødvendig forutsetning for matematikkens utvikling var skrivekunsten, som gjorde at en kunne skrive tall og relasjoner mellom tallene på en systematisk måte.
De første jordbrukssamfunnene utviklet seg rundt de store elvene Nilen, Eufrat og Tigris, Indus, Chang Jang og Huang He, og disse samfunnene trengte former for matematisk kunnskap for å kunne fungere. Det er derfor naturlig at vi fra disse samfunnene har de første systematiske nedtegnelsene av matematisk kunnskap. Først og fremst måtte en ha en godt utviklet kalender, slik at en kunne vite når det er tid for å så og høste. For å kunne lage en kalender, trengtes foruten kunnskap om tall og aritmetikk, omfattende astronomiske kunnskaper. Kunnskaper innenfor astronomi utvikles gjennom matematiske beregninger. Et jordbrukssamfunn har også behov for å kunne utføre landmåling, slik at en kan fordele landområdene mellom bøndene. Landmåling krever geometrisk kunnskap, og ordet «geometri» betyr da også landmåling. Det var behov for å kartlegge og beregne regelmessige elveflommer, slik at en kunne sikre seg mot for store tap av avling og menneskeliv. Etter en flom måtte en ofte måle opp bøndenes landområder på nytt, for flommene medførte gjerne endringer i landskapet. Historiske kilder viser at alle sivilisasjoner har utviklet matematisk kunnskap for å løse praktiske problemer, i forbindelse med bokføring, astronomi, jordbruk og konstruksjon.
Matematikk i oldtidens Egypt (ca. 1850–600 f.Kr.)
Utdypende artikkel: Oldtidens egyptiske matematikk

Fram til forskerne klarte å tyde de babylonske leirtavlene, var Egypt den rikeste kilden man hadde til kunnskap om matematikk i oldtiden. De eldste funnene av skrevne tall er fra ca 3300 f.Kr., i form av hieroglyfer hogd i ben, sten og metall.[6] Egypterne brukte et titallsystem, men en har også funnet spor av system basert på 5, 12, 20 og 60. Tallsystemet hadde symboler for 1, 10, 100, 1 000, 10 000, 100 000 og 1 000 000. Det eldste systemet var rent additivt, det vil si at et tall kunne leses som summen av flere symboler plassert ved siden av hverandre. Etter hvert ble systemet også multiplikativt, slik at for eksempel tallet 120 000 kunne skrives med to symbol, som 120 og 100 plassert ved siden av hverandre.[6]
Egypterne hadde en kalender der året var delt inn i 12 måneder, hver på 30 dager. I tillegg hadde en fem festdager, slik at året var 365 dager. Også konstruksjon og plassering av pyramidene vitner om at egypterne hadde et høyt utviklet system for telling og måling. For å kunne lage konstant helning på pyramidesidene hadde en for eksempel laget seg et mål tilsvarende dagens cotangens.
De viktigste kildene til egyptisk matematikk er papyrusruller, skrevet med blekk i hieratisk skrift, en forenklet, rundet form for hieroglyfer. Blant disse rullene er Rhind-papyrusen den viktigste. Denne er tidfestet til ca. 1550 f.Kr.,[7] men teksten indikerer at det er en kopi av et eldre dokument, sannsynligvis fra Mellomriket 2000 - 1800 f.Kr.[8] Rhind-papyrusen er antageligvis skrevet som en lærebok i aritmetikk og geometri, og rullen inneholder en beskrivelse av metoder for brøkregning, multiplikasjon og divisjon samt problemer tilsvarende en enkel form for ligninger. Brøkregningen var i hovedsak begrenset til bruk av stambrøk, det vil si brøk med tallet 1 i teller (egyptiske brøker). Egypterne brukte imidlertid også brøken 2/3 og en sjelden gang brøker av typen .[8] Rhind-papyrusen inneholder to tabeller, der ulike brøker skrives som en sum av stambrøker. I tillegg inneholder rullen 84 problemer med løsning, de fleste av matematisk karakter. Den grunnleggende operasjonen var addisjon. Multiplikasjon kunne utføres ved et system basert på dobling og summasjon. Divisjon brukte brøktabellene, sammen med en form for dobling av divisor.[8]
Rhind-papyrusen beskriver også praktiske geometriske problem knyttet til beregning av areal og volum. I ett av problemene hevdes det at arealet av en sirkel med diameter 9 enheter er det samme som en firkant med sidekant 8 enheter. Dette gir et uttrykk for π svarende til . Det er ikke funnet bevis for at egypterne kjente til den pytagoreiske læresetningen,[8] selv om Berlin-papyrusen kan indikere en form for kjennskap.[9]
Moskva-papyrusen (ca. 1890 f.Kr.) er eldre enn Rhind-papyrusen, men ikke så innholdsrik. Papyrusen inneholder 25 matematiske problemer, og løsningen til ett av problemene viser at egypterne kunne beregne volumet av en frustum, det vil si en avkortet pyramide.[10] Et annet problem gjelder beregning av arealet av en krummet flate, men teksten gir en uklar beskrivelse av flaten dette gjelder.
Greske matematikere arvet kunnskap fra Egypt, og Aristoteles ga egypterne æren for å ha «oppfunnet» geometrien.[8] Egypterne var imidlertid primært opptatt av praktiske problem, og egyptiske kilder gir aldri forklaringer på hvordan en har kommet fram til en problemløsning og heller ikke bevis for noen av resultatene.
Babylonernes matematikk (ca. 1800–300 f.Kr.)
Utdypende artikkel: Babylonsk matematikk
Babylonsk matematikk refererer til matematikk fra det gamle Mesopotamia (dagens Irak), helt fra de tidligste sumeriske kulturene til begynnelsen av hellenismen. Karakteristikken «babylonsk matematikk» blir brukt på grunn av den viktige rollen byen Babylon hadde i denne perioden. Likevel kan begrepet til en viss grad være misvisende, for den mesopotamiske kulturen omfattet mye mer enn Babylon og tilgrensende områder.[11]
Kunnskapen om de gamle mesopotamerne og de sumeriske kulturene har man fra en svært rik samling av leirtavler med kileskrift. Tavler med matematisk kunnskap kommer fra to vidt forskjellige tidsperioder, de fleste i fra den gammelbabylonske perioden (1900–1600 f.Kr.), men også noen i fra Selevkideriket (323–60 f.Kr.). Samlet vitner tavlene om en rik kultur med en høyt utviklet matematikk.
I Mesopotamia ble et tallsystem basert på grunntall 10 svært tidlig fortrengt av et seksagesimalsystem med grunntall 60. Tall under 59 ble skrevet i et system tilsvarende det egypterne brukte, mens tall over 60 ble behandlet svært annerledes. Babylonerne utviklet et posisjonssystem, der plasseringen av tall i forhold til hverandre var viktig. I et stort tall ble tallene skrevet gruppevis, der første gruppe av tall markerte antall enere, neste gruppe antall ganger grunntallet , neste gruppe ganger grunntallet i andre potens og så videre. Eksempelvis kunne tallet 3785 skrives som . Rester av dette seksagesimalsystemet har vi ennå i dag, i inndelingen av tid og av gradesirkelen.
Det eldste babylonske posisjonssystemet manglet symbol for tallet null. Bare ut fra sammenhengen har en senere vært i stand til å gjette seg til om en tegngruppe var ment å representere eller for eksempel . Først i tavler fra Selevkideriket dukker det opp et tegn for å markere en tom plass mellom to grupper av tall, slik at en for eksempel kunne skrive tallet . Tegnet ble ikke brukt i slutten av et tall og ikke brukt alene, så babylonsk matematikk fikk aldri et fullgodt symbol for null.[12]
Posisjonssystemet ble også brukt for å uttrykke brøker av typen . Posisjonssystemet gjorde babylonerne i stand til å utføre multiplikasjon og divisjon langt mer effektivt enn det egypterne var i stand til, og operasjoner på brøker var like enkelt som operasjoner på heltall.
Babylonsk matematikk var i stor grad basert på bruk av tabeller, og i tavler har en funnet multiplikasjonstabeller, divisjonstabeller, tabeller for regning med desimalbrøker, tabeller for kvadrat- og kubikktall, og også tabeller for kvadratrøtter og kubikkrøtter. Lineær interpolasjon ble brukt til å finne mellomliggende verdier i tabellene.
Selv om tabellene var viktige, så utviklet babylonerne også prosedyrer eller algoritmer for å løse matematiske problem. De var vel fortrolige med både lineære og kvadratiske ligninger, og i mange tilfeller var de også i stand til å redusere høyere ordens algebraiske ligninger til kvadratiske ligninger. De utviklet en metode for å finne tilnærmede uttrykk for kvadratrøtter. Ved hjelp av brøkuttrykk greide en for eksempel å uttrykke roten av 2 som , med en feil på rundt 0,000008![12]
Den babylonske leirtavlen som er mest kjent har fått navnet Plimpton 322, laget omkring 1800 f.Kr.[13] Leirtavlen inneholder blant annet av en tabell med pytagoreiske tripler, det vil si tre tall som oppfyller ligningen . Babylonerne kjente til den pytagoreiske setningen mer enn tusen år før Pytagoras levde. Organiseringen av de pytagoreiske triplene på tavlen kan også indikere en tidlig form for trigonometri.
Tradisjonelt har en framstilt babylonerne som pionerer i algebra og egypterne som grunnleggere av geometri. Mange tavler med kileskrift kan imidlertid vitne om at babylonerne var kommet vel så langt i geometri som egypterne.[12]
Kinesisk matematikk (etter ca. 1300 f.Kr.)
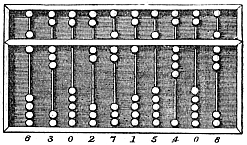
De tidligste bevarte kilder til kinesisk matematikk stammer fra tall som er risset inn på skilpaddeskall (såkalte orakelben). Disse stammer fra Shāng-dynastiet (ca. 1500–1027 f.Kr.). Disse tallene er skrevet i et posisjonssystem, slik at tallet 123 er skrevet (fra topp til bunn) med symbolet for 1 一 fulgt av symbolet for 100 百, deretter symbolet for 2 二 fulgt av symbolet for 10 十, og til sist symbolet for 3 三 (sammen 一百二十三). Dette tallsystemet er fortsatt i bruk i kinesisk skriftspråk, ved siden av arabiske tall. Det kunne gjøres raske og avanserte utregninger ved hjelp av en suànpán, som er en kinesisk kuleramme. Denne oppfinnelsen ble trolig utviklet til praktisk bruk av handelsmenn og gav en «regnekraft» som ikke ble passert før kalkulatorens oppfinnelse.
I 212 f.Kr. beordret Qín-dynastiets keiser Shǐ Huáng at alle bøker skulle brennes. Selv om denne ordren ikke ble fulgt overalt, er konsekvensen at man i dag har få sikre kilder om matematikken i det gamle Kina.
Under Táng-dynastiet ble den til da kjente matematiske viten samlet i verket Ti klassikere om matematikk (Suànjīng shíshū, 算经十书). Den mest innflytelsesrike av disse ti er Matematikk i ni kapitler (Jiǔzhāng suànshù), skrevet av en anonym forfatter for 2000 år siden. Den inneholder praktiske løsninger på matematiske problem, uten bruk av avansert deduksjon, slik samtidig gresk matematikk tilstrebet. Flere av bokas beviser ble ikke oppdaget i Europa før over tusen år senere.[14] De fleste matematiske problem var knyttet til renteregning, skattlegging, rekker, geometri og landmåling. En kinesisk matematiker var den første som klarte å beregne tallet π med hele 7 desimaler.
Eksamenssystemet for statstjenestemenn var enerådende karrierevei for personer med høyere utdanning fra Sòng-dynastiet og senere. Disse harde eksamenene vektla kun kunnskap om konfusianske klassiske tekster. Derfor var studier av matematikk kun en distraksjon fra eksamenspresset, som det ikke lønte seg å vie tid til. Dette er en mulig forklaring på at kinesisk matematikk senere kom til å miste sitt forsprang.[15] Man holdt seg med et matematisk-astronomisk direktorat som hadde som hovedoppgave å beregne kalenderen, men kalenderoppsettene ble mer og mer upålitelige, inntil europeiske jesuitter med matematisk utdannelse ble engasjert på 1600-tallet.[16]
Indisk matematikk (ca. 900 f.Kr.–1150 e.Kr.)
India har en lang og spennende historie, også som matematikk-nasjon. Landet har fostret mange store matematikere, fra det 9. århundre, via den store Brahmagupta (598–670) til vår tids Srinivasa Aiyangar Ramanujan (1887–1920), som blir regnet som et av Indias største matematiske genier.
I det 9. århundre før vår tidsregning, blir verdien til π angitt med to desimaler i teksten Shatapatha Brahmana. Sulba Sutraene (ca. 800–500 f.Kr.) var geometriske tekster, og her finner man irrasjonale tall, primtall og kubikkrot. Her finner man også roten av 2 utregnet med fem desimaler. Teksten ga også en metode for å finne sirkelens kvadratur, den løste lineære og kvadratiske ligninger, utviklet pytagoreiske tripler algebraisk, og den ga et numerisk bevis for Pytagoras' læresetning. I det 5. århundre f.Kr. ble de grammatiske reglene for sanskrit utformet av Pāṇini. Hans notasjon var ikke ulik moderne matematisk notasjon, og den tok i bruk metaregler, transformasjoner og rekursjoner på en sofistikert måte. På mange måter kan derfor Paninis arbeid regnes som forløperen til moderne grammatisk teori, som er viktig i programmeringsspråk.
I verk av Pingala (omkring det 3.–1. århundre f.Kr.) finner man matematiske ideer som kan regnes som forløpere for det binære tallsystem, binomialformelen og fibonaccitall.
Mellom 300 f.Kr. og 200 e.Kr. begynte tilhengere av jainismen å studere matematikk for matematikkens egen skyld. De var de første til å utvikle blant annet transfinite tall, gruppeteori, logaritmer, tredjegradsligninger, fjerdegradsligninger, permutasjoner og kombinasjoner.[trenger referanse] Bakshali-manuskriptet, som ble skrevet en gang mellom 200 f.Kr. og 200 e.Kr., inneholder løsningene på lineære ligninger med opp til fem ukjente, løsning av andregradsligninger, aritmetiske og geometriske rekker, bruk av null og negative tall, og mye mer. Her kan man også finne nøyaktige utregninger av irrasjonale tall. Noen av disse utregningene innebærer at en må trekke ut kvadratroten av tall på størrelse med en million, og røttene er regnet ut med minst 11 desimaler.
Brahmagupta (598–668) var en markant indisk matematiker, og han blir ofte kreditert oppdagelsen av tallet null.[trenger referanse] I sitt verk Brahma Sphuta Siddhanta fra ca. 628 presenterer han regler for regning med negative tall og null. Han er også kjent som den første som ga den generelle løsningen til den diofantiske ligningen på formen ax + by = c. Han etterlot seg også en rekke matematiske problem som var formulert på en kunstferdig måte, slik de indiske matematikerne ofte gjorde.
En av tidenes største indiske matematikere var Bhaskara (1114–1185). I tillegg til sine arbeid innen aritmetikk, algebra og trigonometri, er han en av forløperne for moderne matematisk analyse. Han hadde stor forståelse for differensial- og integralregning lenge før Newton og Leibniz la det formelle grunnlaget for matematisk analyse. Bhaskaras mest kjente verk var Lilivati, oppkalt etter hans eneste datter.
Grekernes matematikk (ca. 550 f.Kr.–300 e.Kr.)

Grekerne leverte mange viktige bidrag til utviklingen av matematikk, og den aller viktigste var nok innføringen av det matematiske beviset. Tidligere sivilisasjoner hadde også hatt en høyt utviklet matematikk, men da stort sett i form av mer eller mindre velutviklete algoritmer for å løse bestemte problem og gjøre ulike utregninger. For de greske matematikerne var det ikke lenger nok bare å regne seg fram til en numerisk løsning på problemene, en måtte også bevise at svaret var riktig. En stor del av den kjente matematikken fra antikken ble sammenfattet omkring 300 f.Kr av Euklid i verket Elementer. Her ser man for første gang en strengt oppbygd matematikk som starter med definisjoner og aksiomer, og ut fra disse blir alle de matematiske setningene bevist. Dette verket har stor betydning for utviklingen av matematikken, og det har blitt brukt som læreverk i geometri ved universitetene helt fram til vår tid.
Den første greske matematikeren som nevnes i historiske kilder er Tales fra Milet. Han regnes også som den første greske filosof og vitenskapsmann generelt. En av de mange historiene som er nedtegnet om Tales, er at han ved hjelp av beregninger kunne forutsi en solformørkelse i 585 f.Kr.[17] Han ble blant annet kreditert oppdagelsen av at diameteren deler sirkelen i to like store deler og at alle vinklene i en likesidet trekant er like store.

Den greske matematikeren som er best kjent i dag er nok Pytagoras. Pytagoras var fra øya Samos like ved kysten av dagens Tyrkia, og han slo seg etter hvert ned i en liten gresk by i det sørlige Italia. Her hadde han en gruppe disipler rundt seg, og denne gruppen ble senere kalt pytagoreerne. Dette var en religiøs og filosofisk skole som det er knyttet mange historier og myter til. Pytagoreerne var svært opptatt av tall, og Pytagoras blir ofte tillagt sitatet: «Alt er tall». Pytagoras oppdaget også forholdet mellom harmoniske toner i musikk. Den mest kjente setningen som knyttes til Pytagoras er nok likevel den såkalte Pytagoras’ læresetning. Denne setningen viser en viktig sammenheng i alle trekanter som har en rett vinkel. Hvis du kvadrerer (multipliserer med seg selv) de to korteste sidene (katetene) i en rettvinklet trekant og adderer de to tallene du får, så blir dette like mye som kvadratet av den lengste siden i trekanten (hypotenusen). Denne setningen kan også brukes for å vise at en trekant er rettvinklet.
I moderne matematisk analyse er uendelig små størrelser sentrale. Grunnlaget for den tenkningen man finner der ble lagt allerede hos Zenon fra Elea (ca. 490–425 f.Kr.). Han er særlig kjent for sine paradokser. Et av paradoksene har utgangspunkt i at man kan dele et linjestykke i uendelig mange biter. For at man skal komme fra et punkt til et annet på et linjestykke må man først bevege seg halvparten av veien. For å komme dit, må man først bevege seg halvparten av dette nye linjestykket, og slik fortsetter det. Resultatet, ifølge Zenon, er at all bevegelse vil være umulig.[18]
Perikles var nok mer kjent som filosof og naturvitenskapsmann enn som matematiker, men hans navn knyttes likevel til et av de store problemene i matematikkens historie. Dette gjelder problemet med sirkelens kvadratur. Problemet dreier seg om å konstruere (med passer og linjal) et kvadrat som har samme areal som en gitt sirkel.
To av de aller største greske tenkere, Platon og Aristoteles, leverte ikke selv viktige resultater i matematikk, men de har likevel hatt innflytelse på utviklingen av matematikken i antikkens Hellas. Begge grunnla sine skoler, hvor det blant annet ble undervist i matematikk, og noen av deres elever har hatt stor betydning for matematikkens utvikling. Platon så på matematikk som en del av den oversanselige virkeligheten, og han mente at matematikken dermed var opphøyet over alle de andre vitenskapene. Dette synet var Aristoteles uenig i.[19]
En av Platons elever, Eudoksos, leverte viktige bidrag til astronomien, og han laget også en permanent kalender. Han skal også ha vist at volumet av en kjegle er en tredjedel av volumet til en sylinder med samme grunnflate og høyde, og at volumet til en pyramide er en tredjedel av volumet til et prisme med samme grunnflate og høyde. Dette klarte han ved bruk av utfyllingsmetoden.
I hellenismen ble den greske matematikken videreutviklet med hovedsete i Alexandria. Her levde den store Euklid, som skrev læreverket Elementer. Dette verket inneholder ikke bare geometri, men også viktige resultater fra andre deler av matematikken. I den hellenistiske tidsalderen leverte også Arkimedes viktige bidrag til matematikken. I likhet med Fermat offentliggjorde han ofte sine resultater uten bevis, slik at andre matematikere kunne ha fornøyelsen av å finne det ut selv.[20]
Den siste av de store greske geometrikerne var Apollonios fra Perge (ca. 262–190 f.Kr.). Han er særlig kjent for sine teorier om kjeglesnitt, og hans mest kjente verk er Conica (som betyr kjeglesnitt). Et kjeglesnitt kan defineres som snittet mellom en kjegle og et plan, og Apollonios var den første som innså at en kan få alle typer kjeglesnitt ved å skjære en fast kjegle med et varierende plan. Tidligere hadde en bare sett på rette kjegler. Apollonios innførte også navnene ellipse, parabel og hyperbel.[21]
En av de siste betydningsfulle greske matematikerne var Diofant, også kalt Diofantos fra Alexandria. Han skal ha hatt sitt virke omkring år 250, og hans mest kjente verk er Aritmetika. Dette verket har hatt stor betydning for utviklingen av matematikk helt fram til våre dager, og den hadde stor påvirkning på en matematiker som Fermat. Her beskriver Diofant hvordan en kan generere alle primitive pytagoreiske tripler, og det var i margen av dette avsnittet i boken at Fermat skrev sin berømte kommentar som senere har blitt kalt Fermats siste teorem.
Persisk og arabisk matematikk (ca. 700–1600)
Utdypende artikkel: Matematikk i middelalderens islam
På 700-tallet erobret araberne store deler av Midtøsten, Nord-Afrika, Den iberiske halvøy og deler av India, og araberne ga flere viktige bidrag til utviklingen av matematikken.
Selv om de fleste islamske tekster om matematikk ble skrevet på arabisk, var ikke alle skrevet av arabere. På denne tiden var arabisk et utbredt skriftspråk blant lærde i de delene av verden som araberne hadde erobret, på samme måte som gresk var et utbredt språk i den hellenistiske verden. Noen av de viktigste matematikerne innenfor den muslimske verden var persere.
En av de mest kjente arabiske matematikerne var Muḥammad ibn Mūsā al-Ḵwārizmī, som levde på 800-tallet i Persia. Han skrev flere viktige bøker. De viktigste tekstene hans var om de hindu-arabiske tallene og om metoder for å løse ligninger. Ordet algoritme er utledet av hans navn, og ordet algebra stammer fra tittelen på ett av hans mest kjente verk: Al-Jabr wa-al-Muqabilah. Al-Khwarizmi blir ofte sett på som grunnleggeren av moderne algebra.
En videre utvikling av algebra finner man hos Abu Bakr al-Karaji (953–1029) i hans bok al-Fakhri. På 900-tallet ble verkene til Diofant oversatt fra gresk til arabisk av Abu l-Wafa.
Omar Khayyām – en persisk dikter som levde på 1100-tallet – var også matematiker, og han skrev blant annet en bok hvor han tok for seg svakhetene i Euklids Elementer. Han ga også en geometrisk løsning på kubiske ligninger, som blir regnet som en av de mest originale bidragene fra datidens matematikk. Han hadde også sterk innflytelse på kalenderreformene. Som matematiker var Khayyám kjent for å ha funnet en metode for å løse tredjegradsligninger ved en geometrisk metode. I 1070 skrev han sitt mest kjente verk om algebra, hvor han klassifiserte ligninger etter graden. Her presenterte han også en metode for å løse andregradsligninger som er svært lik den vi bruker i dag.
Nyere forskning har rettet oppmerksomheten mot den store dybden i den arabiske matematikken. Mange av de ideene som tidligere ble sett på som nyvinninger av europeiske matematikere på 1500-tallet, 1600-tallet og 1700-tallet ble i virkeligheten utviklet av arabiske matematikere omkring fire århundre tidligere. På mange måter ligger den matematikken som studeres i dag mye nærmere den arabiske matematikken enn den gamle greske matematikken.
Middelalder i Europa
Mens den arabiske matematikken blomstret helt fram til slutten av 1400-tallet, var det lite matematisk aktivitet i Europa. Ett av unntakene i den tidlige middelalderen var Alkuin fra York (735–804). Han fikk i oppgave å undervise Karl den store og hans familie i retorikk, logikk, teologi og matematikk. Han skrev elementære bøker i aritmetikk, geometri og astronomi, og han bygde opp en katedralskole i Tours. Denne ble en forløper for de franske universitetene. Han skrev lærebøkene i form av spørsmål og svar, og de inneholder flere klassiske matematiske problemer.
I høymiddelalderen skjer en oppvåkning i Europa, og mange av de greske filosofene blir gjenoppdaget. Det oppstår blant annet en ny interesse for Aristoteles' logikk, og i denne perioden utvikles også skolastikken.
På 1200-tallet var flere regnebøker i bruk i Europa, og blant dem finner man også Algorismus i Hauksbok. Hauksbok ble skrevet av Haukr Erlendsson, som var lagmann på Island i 1294 og kom til Norge i ca. 1301. En del av denne boken kalles for Algorismus, og dette er den eldste regneboken på noe nordisk språk. Boken starter med å beskrive posisjonssystemet, og den fortsetter med å beskrive de ulike regneartene, kvadratrot og kubikkrot.
På 1200-tallet levde også Leonardo av Pisa, også kalt Fibonacci, og det er fra ham man har fått kunnskapen om de såkalte fibonaccitallene. Leonardo var godt kjent med den arabiske matematikken, og han er blant annet kjent for å ha brakt arabernes algebra til Europa. Han var også den første av de italienske regnemestrene (maestri d'abbaco), som blant annet underviste handelsfolk i regning. På denne tiden skjer en forsiktig oppblomstring av matematikken i Europa.
Gjennombruddet i Europa

Den matematiske tradisjonen ble gjenopptatt i Europa etter middelalderen. Dette ble i stor grad gjort mulig av Adelards oversettelser fra 1100-tallet av arabiske verk til latin. Utviklingen skjøt fart i 1500-tallets Italia, da blant andre Girolamo Cardano leverte viktige bidrag til utviklingen av algebra og løsing av ligninger. De italienske fremgangene førte til økt entusiasme for forsking i matematikk, og dette spredde seg til resten av Europa. René Descartes tillempet algebraen til geometriske problem, og Pierre de Fermat og Blaise Pascal var sentrale i utviklingen av sannsynlighetsregningen.
Matematikken fikk en betydelig rolle i sammenheng med den vitenskapelige revolusjonen som startet omkring 1600, da Johannes Kepler og Galileo Galilei anvendte matematiske sammenhenger for å beskrive fysiske fenomen. Den skotske matematikeren Lord Napier var den første som utforsket naturlige logaritmer. På 1600-tallet ble også grunnlaget for den matematiske analysen lagt. Dette dreier seg om forholdet mellom størrelser som gjennomgår forandring, og det er et viktig problemløsingsverktøy innenfor andre grener av vitenskapen og teknikk. Analysen ble grunnlagt av Leibniz og Newton, som gjorde viktige fremskritt uavhengig av hverandre. Newton brukte siden analysen for å formulere den klassiske mekanikken.
Parallelt med matematikkens økende anvendelser ble den også utviklet stadig mer i abstrakt retning. På 1700-tallet og 1800-tallet skjedde en nærmest eksplosjonsartet vekst av matematisk kunnskap. Det var på denne tiden nye områder som topologi, analytisk tallteori og analytisk geometri ble utviklet.
Moderne utvikling
1700-tallet
Kunnskapen om de naturlige tallene: 1, 2, 3, ... er eldre enn noen skrevne tekster, og de tidligste sivilisasjoner i Mesopotamia, Egypt, India og Kina kjente til regning med disse tallene (aritmetikk). En måte å se på utviklingen av de ulike tallsystemene i moderne matematikk er å se på hvordan nye tall blir studert for å finne svar på spørsmål knyttet til regning med de gamle tallene. I tidligere tider ga brøker (rasjonale tall) svaret på spørsmål av typen: Hvilket tall er det som multiplisert med 3 gir svaret 1? I India og Kina, og mye senere i Tyskland, ble negative tall utviklet for å gi svaret på spørsmålet: Hva får du når du trekker et stort tall fra et som er mindre? Nullen ble funnet opp på bakgrunn av et lignende spørsmål: Hva får du når du trekker et tall fra seg selv?
Et annet naturlig spørsmål er hva slags tall kvadratroten av to er. Grekerne visste at dette ikke var en brøk, men et bedre svar på spørsmålet kom da irrasjonale tall ble funnet opp. De ble utviklet av John Napier og senere videreutviklet av Simon Stevin. Ved å bruke desimaler og en ide knyttet til grensebegrepet, studerte Napier en ny konstant. Denne konstanten ga Leonhard Euler senere navnet .

Euler hadde stor innflytelse på standardiseringen av andre matematiske begrep og notasjoner. Han ga kvadratroten av minus 1 symbolet , og han populariserte også bruken av den greske bokstaven for å beskrive forholdet mellom sirkelens omkrets og dens diameter. Senere utviklet han følgende viktige identitet i matematikken,
kjent som Eulers likhet.
1800-tallet
I løpet av 1800-tallet ble matematikken stadig mer abstrakt. I dette århundret levde en av tidenes største matematikere, Carl Friedrich Gauss, og også to av de største norske matematikerne: Niels Henrik Abel og Sophus Lie. Gauss leverte det første fullstendige beviset på algebraens fundamentalteorem, og både Abel og Lie ga flere viktige bidrag til algebraens utvikling.
En viktig oppdagelse på 1800-tallet var da Nikolaj Lobatsjevskij og Janos Bolyai uavhengig av hverandre oppdaget den ikke-euklidske geometrien. I deres hyperbolske geometri krummer rommet slik at det finnes uendelig mange linjer gjennom et gitt punkt som er parallelle med en gitt linje. Bernhard Riemann, en av elevene til Gauss, leverte også et viktig bidrag til utviklingen av den ikke-euklidske geometrien. Hans utvidelse av differensialgeometrien har fått navnet Riemann-geometri. Her utvidet han den tradisjonelle differensialgeometrien til dimensjoner. Den ikke-euklidske geometrien kom som en overraskelse, da man trodde at det bare fantes én geometri, nemlig den euklidske. Den euklidske geometrien er den som stemmer best overens med den menneskelige intuisjon, men paradoksalt nok viste Albert Einstein på starten av 1900-tallet gjennom sin relativitetsteori at det er den ikke-euklidske geometrien som beskriver virkeligheten.
I tillegg til nye retninger av matematikken, fikk matematikken et strengere logisk fundament. Dette skjedde blant annet innenfor matematisk analyse, hvor Augustin Louis Cauchy og Karl Weierstrass leverte viktige bidrag på dette området.

På 1800-tallet ble også en ny retning innen algebra utviklet, nemlig boolsk algebra. Den ble utviklet av den engelske matematikeren George Boole. I boolsk algebra kan variablene kun ha to tilstander eller verdier. Enten er de sanne med verdien 1, eller de er usanne med verdien 0. Boolsk algebra fikk stor betydning i det 20. århundre, og det er denne matematikken som blir brukt i moderne datamaskiner.
Matematikkens begrensning ble også utforsket på 1800-tallet. Niels Henrik Abel ga det endelige beviset for at ligninger av høyere grad enn fire ikke kan løses med vanlige algebraiske metoder. Andre matematikere på denne tiden viste at passer og linjal ikke er nok for å tredele en tilfeldig vinkel (vinkelens tredeling), og heller ikke for å konstruere et kvadrat med samme areal som en gitt sirkel (sirkelens kvadratur). Dette var to problemer som matematikere hadde forsøkt å løse siden antikken.
Oppdagelsene til Abel og Galois la videre grunnlaget for utviklingen av gruppeteori og abstrakt algebra. På 1900-tallet har fysikere og andre vitenskapsmenn oppdaget at gruppeteori er en ideell måte å studere symmetri.
1900-tallet
I løpet av 1900-tallet har matematikken utviklet seg stadig videre. Matematikere er ettertraktet innen mange områder, både innenfor undervisningssektoren og i industri og næringsliv. Årlig blir det delt ut hundrevis av doktorgrader i matematikk og fagfeltet har vokst med slik fart at det er svært vanskelig å holde oversikten.
På bakgrunn av de foregående århundrenes fremskritt forsøkte matematikerne tidlig på 1900-tallet å gjennomføre en fullstendig formalisering av matematikken. Målet var å utlede alle matematiske sannheter ved hjelp av enkle og veldefinerte logiske regler, og eventuelt finne en metode for å utlede matematiske sannheter «mekanisk». En av lederne for dette arbeidet var David Hilbert, som var en av de fremste matematikerne på denne tiden. Han presenterte et program for å videreutvikle og formalisere matematikken. Han ønsket å konstruere et matematisk system basert på noen grunnleggende aksiomer. Ved hjelp av dette systemet skulle alle setninger og problemer i matematikken kunne bevises, og systemet skulle være konsistent. Hvis en beviste at en setning var sann med én metode, skulle en altså ikke kunne finne en annen metode som beviste at den samme setningen var usann. Dette arbeidet samlet flere av de fremste matematikerne i første del av 1900-tallet.
Gottlob Frege viet mange år av sin yrkesaktive karriere til å formulere grunnreglene for aritmetikken med basis i mengdelæren. Like før han skulle gi ut sitt store verk, oppdaget den britiske matematikeren og filosofen Bertrand Russell en inkonsistens i Freges system. Denne inkonsistensen har fått navnet Russells paradoks, og den representerte en alvorlig fare for drømmen om et fullkomment matematisk system.
I 1931 snudde Kurt Gödel hele det rådende matematiske verdensbildet på hodet ved å bevise at ethvert formelt system enten er utilstrekkelig eller fører til selvmotsigelser.[22] Dette medfører ikke at de matematiske setningene som allerede er bevist blir ugyldige, men Gödels oppdagelse viser at det er enkelte setninger og problemer som ikke kan bevises i matematikken. Som en følge av dette begynte matematikere å forsøke å finne ut hvilke setninger som ikke kunne bevises, og man så ikke bort fra at Fermats siste setning kunne være et slikt ubeviselig problem.[23] Da den britisk-amerikanske matematikeren Andrew Wiles i 1995 presenterte et bevis på dette 350 år gamle problemet, var det et av århundrets aller viktigste resultater i matematikken.

Under 2. verdenskrig fikk matematikerne en viktig rolle som kodeknekkere. Et av de mest kjente navnene i denne forbindelsen var Alan Turing. En periode var han leder for det britiske sjøforsvarets Enigmaseksjon ved Bletchley Park. Her jobbet en gruppe dyktige matematikere for å knekke kodene på de tyske meldingene. Tyskerne hadde utviklet en avansert elektromagnetisk krypteringsmaskin, kalt Enigma, som de brukte for å kode meldinger de sendte. Den innsatsen Turing og hans gruppe gjorde for å knekke disse kodene spilte en viktig rolle for krigens utvikling. Turing var også med på å konstruere en av de første programmerbare datamaskinene.
I 1944 lanserte John von Neumann begrepet spillteori. Her brukte han matematikken som redskap for å analysere strukturen i ulike spill, og hvordan mennesker spiller disse spillene. Matematisk spillteori ble et viktig verktøy i forbindelse med militære strategier i den kalde krigen.[24]
På 1900-tallet fikk matematikken nye anvendelser i og med datamaskinenes inntog, og i dag er den matematiske vitenskapen så omfattende og raskt voksende at ingen matematiker kan ha inngående kjennskap til alle delene. Årlig publiseres et hundretusentalls artikler med nye matematiske resultater.
Norsk matematikkhistorie
Den matematiske oppvåkningen i Europa kom lenge etter blomstringstiden i andre deler av verden, og norsk matematikk har en enda kortere historie. I middelalderen skrev Haukr Erlendsson Hauksbók. Denne boken hadde en liten del om regnekunst, som het Algorismus. Her finner man blant annet en forklaring på posisjonssystemet, og boka har også en beskrivelse av syv regnearter: legge til, trekke fra, fordoble, halvere, multiplisere, dele og trekke ut roten.
Caspar Wessel (1745–1818) blir ofte regnet som den første norske matematiker. Wessel var landmåler av yrke, og han var med på å kartlegge Danmark. Gjennom denne kartleggingen fant han opp sine egne metoder som var langt mer effektive enn de gamle. Han jobbet blant annet mye med vektorer, og han er blant de aller første som adderte vektorer. I 1798 publiserte han en avhandling med tittelen Om direktionenes analytiske betegning, et forsøg anvendt fornemmelig til plane og sfæriske polygoners opløsning. Her gir han blant annet en geometrisk beskrivelse av de komplekse tallene, før både Gauss og Argand gjorde det. Arbeidet hans ble ikke oversatt, men hvis det hadde blitt gjort ville han nok blitt regnet blant de største matematikerne i Europa på den tiden.
De to store
Etter Wessel fulgte noen av tidenes største norske matematikere. Først ute var Niels Henrik Abel. Abel var født på Finnøy og oppvokst i Gjerstad, men det var først da han begynte på katedralskolen i Christiania og fikk Bernt Michael Holmboe til lærer at hans matematiske talent begynte å blomstre. Snart hadde Abel gått forbi alle sine lærere i Norge, og han måtte reise utenlands for å lære mer. På en reise i Europa ble Abel kjent med den tyske ingeniøren August Leopold Crelle. Crelle hadde lenge ønsket å starte et matematisk tidsskrift som kunne ta kampen opp med de franske, og etter hvert startet han Journal für die reine und angewandte Mathematik. Her publiserte Abel de fleste av sine arbeider. Abel leverte viktige bidrag til matematikken på flere områder, men han er nok mest kjent for sin ligningsteori, teorien om elliptiske funksjoner og arbeidene om uendelige rekker.

Etter Abel fulgte en annen stor norsk matematiker: Sophus Lie (1842–1899). Lie var høyt ansett i Europa, og han arbeidet blant annet i Berlin, Göttingen og Paris. I Göttingen samarbeidet han med Felix Klein. I 1886 ble Lie utnevnt til professor i matematikk i Leipzig. Lie skapte et helt nytt matematisk begrep, som i dag går under betegnelsen Lie-grupper, og han leverte flere viktige bidrag til utviklingen av algebra.
Samtidig med Sophus Lie levde og virket også Ludvig Sylow. Også han leverte viktige bidrag til gruppeteorien, og de såkalte Sylow-teoremene er oppkalt etter ham. Sylow ble tidlig anerkjent i utlandet, men her hjemme forble han lenge anonym. Da han var ferdig med studiene var det ingen stilling til ham ved Universitetet i Oslo, så han fikk jobb som overlærer i Halden i stedet. Her ble han værende i 40 år. I 1898 ble han utnevnt til ekstraordinær professor ved universitetet, og han underviste her fram til han var nesten 85 år.
Elling Holst (1849–1915) var elev av Sophus Lie, og han studerte geometri under Felix Klein. Holst arbeidet mye med skolematematikken, og han var kjent som en dyktig lærer. Hans doktoravhandling fra 1882 hadde tittelen Et par syntetiske methoder, især til brug ved studiet af metriske egenskaber.
Organiseringen av norsk matematikk
På begynnelsen av 1900-tallet hadde det matematiske miljøet i Norge blitt sterkt, og det oppstod et behov for en samlende organisasjon. I 1918 ble Norsk matematisk forening dannet, og Carl Størmer ble valgt som foreningens første formann. En annen markant matematiker på denne tiden var Thoralf Skolem (1887–1963). Han var også en sentral person i Norsk matematisk forening, han var redaktør for Norsk matematisk tidsskrift, og i 1953 var han med og grunnla tidsskriftet Mathematica Scandinavica.
En av de aller mest markante norske matematikerne i vår tid er nok Atle Selberg. Han er blant annet kjent for sine arbeider innenfor analytisk tallteori, og han regnes som en av de fremste tallteoretikerne gjennom alle tider. I 1950-årene jobbet han med å introdusere spektralteori i tallteorien, og resultatet av dette arbeidet finnes i den såkalte Selbergs sporformel, som er hans mest anerkjente arbeide. I 1950 fikk Selberg den prestisjetunge Fieldsmedaljen, og i 1986 fikk han Wolfprisen i matematikk.
I forbindelse med Abels 200-årsjubileum i 2002 ble Abelprisen opprettet. En slik pris ble foreslått allerede av Sophus Lie, da det ble kjent at nobelprisen ikke skulle deles ut i matematikk. Da Abelprisen første gang ble delt ut i 2003, ble dette etter manges mening den viktigste prisen i matematikk.
Referanser
Litteratur
Eksterne lenker
Wikiwand - on
Seamless Wikipedia browsing. On steroids.


















