
混沌理论
物理学相关理论 / 维基百科,自由的 encyclopedia
混沌理论(英语:Chaos theory)是关于非线性系统在一定参数条件下展现分岔、周期运动与非周期运动相互纠缠,以至于通向某种非周期有序运动的理论。在耗散系统和保守系统中,混沌运动有不同表现,前者有吸引子,后者无(也称含混沌吸引子)。
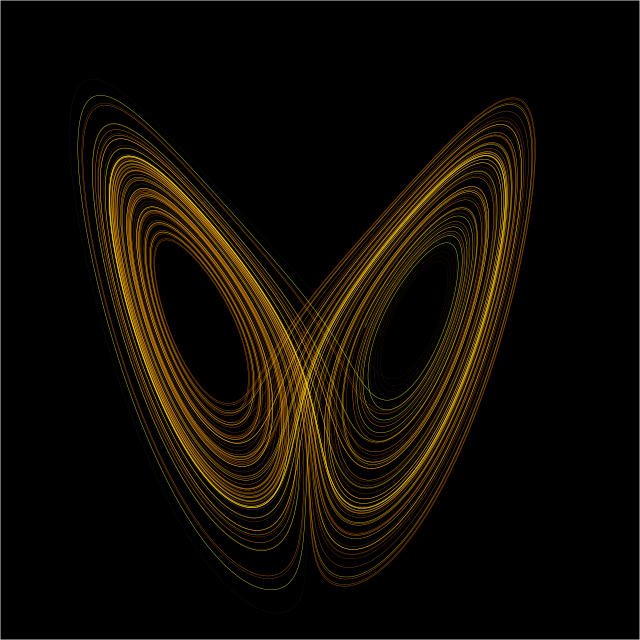





从20世纪80年代中期到20世纪末,混沌理论迅速吸引了数学、物理、工程、生态学、经济学、气象学、情报学等诸多领域学者有关注,引发了全球混沌热。混沌,也写作浑沌(比如《庄子》)。自然科学中讲的混沌运动指确定性系统中展示的一种类似随机的行为或性态。确定性是指方程不含随机项的系统,也称动力系统。典型的模型有单峰镜像迭代系统,洛伦兹微分方程系统,若斯叻吸引子,杜芬方程,蔡氏电路,陈氏吸引子等。为浑沌理论做出重要贡献的学者有庞加莱、洛伦兹、上田睆亮(日语:上田睆亮)、费根堡姆、约克、李天岩、斯美尔、芒德勃罗等。混沌理论向前可追溯到19世纪庞加莱等人对天体力学的研究,他提出了同宿轨道(英语:Homoclinic orbit)、异宿轨道(英语:Heteroclinic orbit)的概念,他也被称为浑沌学之父。
混沌行为可以在许多自然系统中被观测到,例如天气和气候。[1]对于这个行为的研究,可以通过分析混沌数学模型,或者通过诸如递归图(英语:Recurrence plot)和庞加莱映射等分析技术。