Тапалагічная прастора

Тапалагі́чная прасто́ра^[1][2] — мноства з дадатковай структурай пэўнага тыпу (так званай тапалогіяй); з’яўляецца адным з асноўных аб’ектаў (разам з непарыўнымі адлюстраваннямі) вывучэння раздзела матэматыкі пад назвай тапалогія.

Тапалагічная прастора
Вывучаецца ў	агульная тапалогія[d]
Медыяфайлы на Вікісховішчы

Паняцце тапалагічнай прасторы з’явілася як абагульненне метрычнай прасторы^[en], якая, у сваю чаргу, абагульняе паняцці геаметрычнай прасторы і фігур.

Заданне тапалагічнай структуры, або тапалогіі, на мностве дае выразны матэматычны сэнс блізкасці, аддаленасці, аддзялення яго элементаў без выкарыстання лікавай велічыні адлегласці паміж імі.

У сучаснае вызначэнне структуры тапалагічнай прасторы ўвайшоў мінімальны набор уласцівасцяў сістэмы метрычных наваколляў, дастатковы для вызначэння такіх паняццяў, як непарыўнасць, звязнасць і, у большасці выпадкаў, збежнасць у самых агульных сітуацыях, калі метрычныя паняцці могуць быць ужо непрыдатнымі.

Акрамя агульных выпадкаў, калі задаць адлегласць паміж пунктамі немагчыма, выкарыстанне тапалагічнай мовы часта спрашчае разважанні і аб метрычных прасторах, у тых выпадках, калі яны не залежаць ад канкрэтных лікавых значэнняў адлегласці.

Уласцівасці, якія залежаць толькі ад тапалагічнай структуры на мностве, называюцца тапалагічнымі ўласцівасцямі і вывучаюцца ў агульнай тапалогіі. Спалучэнне тапалагічнай структуры з іншымі структурамі, ці ўзбагачэнне яе дадатковымі абмежаваннямі, прыводзіць да вылучэння розных другіх відаў уласцівасцяў, якія вывучаюцца ў іншых раздзелах тапалогіі ці сумежных дысцыплін.

Вызначэнне

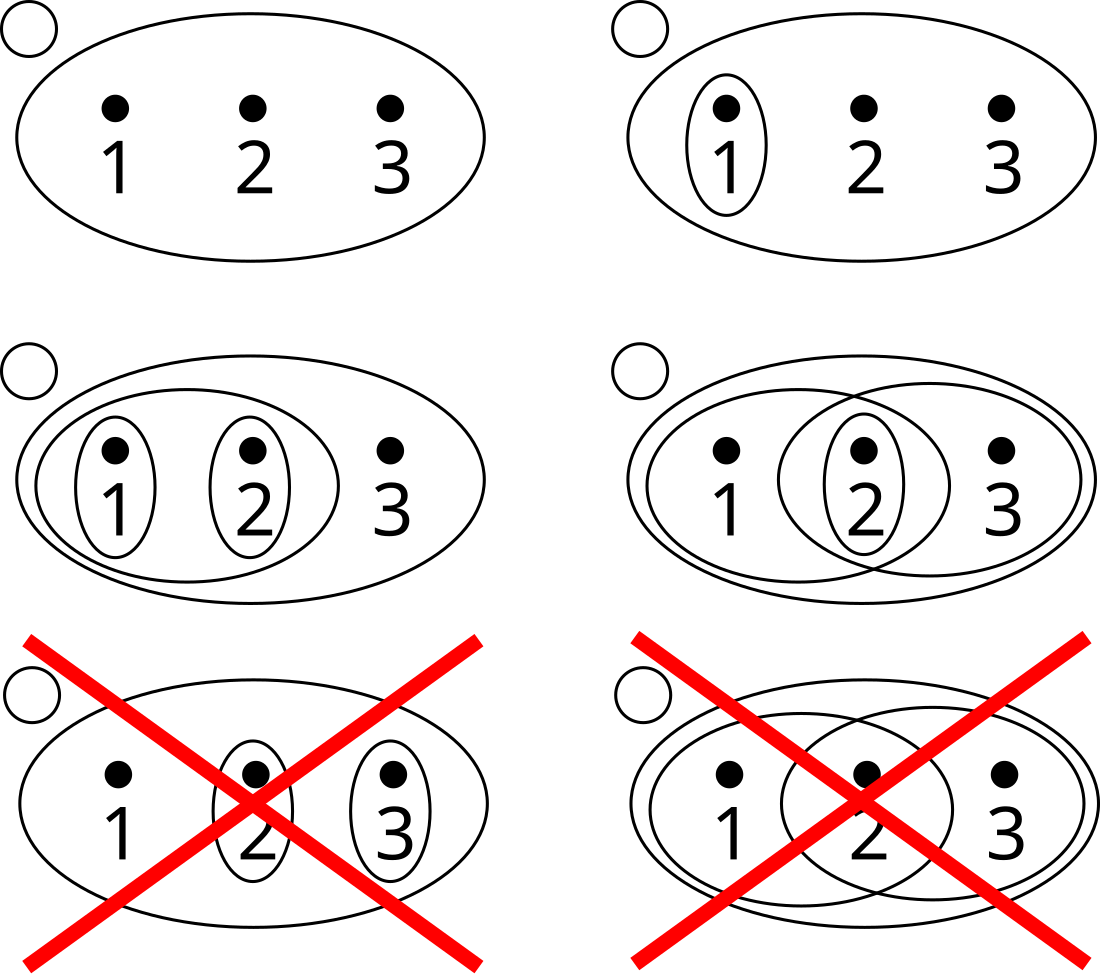
Няхай дадзена мноства ${\displaystyle X}$. Сістэма ${\displaystyle {\mathcal {T}}}$ яго падмностваў называецца тапалогіяй на ${\displaystyle X}$, калі выкананы наступныя ўмовы:

1. Аб’яднанне адвольнага сямейства мностваў, якія належаць ${\displaystyle {\mathcal {T}}}$, належыць ${\displaystyle {\mathcal {T}}}$. Гэта значыць, што калі ${\displaystyle U_{\alpha }\in {\mathcal {T}}\quad \forall \alpha \in A}$, то ${\displaystyle \bigcup \limits _{\alpha \in A}U_{\alpha }\in {\mathcal {T}}}$.
2. Перасячэнне канечнага сямейства мностваў, якія належаць ${\displaystyle {\mathcal {T}}}$, належыць ${\displaystyle {\mathcal {T}}}$. Гэта значыць, што калі ${\displaystyle U_{i}\in {\mathcal {T}}\quad i=1,\;\ldots ,\;n}$, то ${\displaystyle \bigcap \limits _{i=1}^{n}U_{i}\in {\mathcal {T}}}$.
3. ${\displaystyle X,\;\varnothing \in {\mathcal {T}}}$.

Пара ${\displaystyle (X,\;{\mathcal {T}})}$ называецца тапалагічнай прасторай. Мноствы, якія належаць ${\displaystyle {\mathcal {T}}}$, называюцца адкрытымі мноствамі^[en]. Элементы мноства ${\displaystyle X}$, на якім зададзена тапалогія, называюцца, як у геаметрыі, пунктамі.