Средностепенна стойност

Средностепенна стойност (СС) или средностепенно е вид средна стойност на набор от числа в математиката, която се получава чрез повдигане на всички числа на степен ${\displaystyle s}$, намиране на средноаритметичната стойност на тези ${\displaystyle s}$-ти степени и взимане на ${\displaystyle s}$-ия корен от тази средна стойност. Тя обобщава средните стойности, известни от питагорейците като архимедови средни: аритметична, геометрична, квадратична и хармонична, чрез въвеждане на параметъра ${\displaystyle s}$. Затова в чуждоезичната литература се нарича още средно обобщено и генерализирано средно. Във връзка с неравенствата на Хьолдер и Минковски средностепенното също има имената средно на Хьолдер (Ото Хьолдер, 1859 – 1937) и средно на Минковски (Херман Минковски, 1864 – 1909).

Обозначава се с различни символи: ${\displaystyle C_{s}(x),A_{d}(x),H_{p}(x),M_{p}(x),m_{p}(x),\mu _{p}(x)}$ и др.

Средностепенното е частен случай на средното квазиаритметично, известно още като „средно на Колмогоров“ (на руски: среднее Колмогорова).

Разновидност на средностепенното е претегленото средностепенно.

Графика на няколко средностепенни ${\displaystyle C_{s}(1,x)=C_{p}(1,x)}$

Определение

Ако ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ е набор от положителни реални числа и ${\displaystyle s}$ е ненулево реално число, тогава средностепенната стойност с показател ${\displaystyle s}$ на набора от числа е: ^[1][2]

${\displaystyle C_{s}(x_{1},\dots ,x_{n})={\sqrt[{S}]{\frac {x_{1}^{s}+x_{2}^{s}+\dots +x_{n}^{s}}{n}}}={\sqrt[{S}]{\frac {\sum \limits _{i=1}^{n}x_{i}^{s}}{n}}}=\left({\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{s}\right)^{{1}/{s}}.}$

Ако числата от набора ${\displaystyle x_{i}}$ са умножени с поредица от положителни тегла ${\displaystyle w_{i}}$, се дефинира понятието средностепенно претеглено: $${\displaystyle CW_{s}(w_{1}x_{1},w_{2}x_{2},\dots ,w_{n}x_{n})={\sqrt[{S}]{\frac {x_{1}^{s}+x_{2}^{s}+\dots +x_{n}^{s}}{w_{1}+w_{2}+\dots +w_{n}}}}={\sqrt[{S}]{\frac {\sum \limits _{i=1}^{n}x_{i}^{s}}{\sum \limits _{i=1}^{n}w_{i}}}}=\left({\frac {\sum \limits _{i=1}^{n}w_{i}x_{i}^{s}}{\sum \limits _{i=1}^{n}w_{i}}}\right)^{{1}/{s}}}$$

Частни случаи

Визуално изображение на някои от посочените случаи за n = 2 с
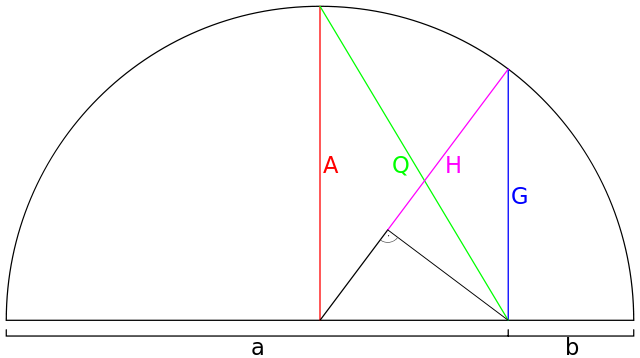
x₁ = a = C_∞ и x₂ = b = C_−∞:

  средно хармонично, H = C₋₁(a, b),

  средно геометрично, G = C₀(a, b)

  средно аритметично, A = C₁(a, b)

  средно квадратично, Q = C₂(a, b)

Средностепенните стойности за ${\displaystyle s=0,\pm 1,2}$ и ${\displaystyle \pm \infty }$ имат свои собствени имена: ^[3]

• ${\displaystyle C_{1}(x_{1},\ldots ,x_{n})=CA={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}}$ се нарича средно аритметично;
  

(с други думи: средноаритметичното на ${\displaystyle n}$ числа е тяхната сума, разделена на ${\displaystyle n}$)

• ${\displaystyle C_{0}(x_{1},\ldots ,x_{n})=\lim _{s\to 0}C_{s}(x_{1},\dots ,x_{n})=CG={\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}}$ е средно геометрично;
  

(с други думи: средното геометрично на ${\displaystyle n}$ числа е ${\displaystyle n}$-ия корен от произведението на тези числа)

• ${\displaystyle C_{-1}(x_{1},\ldots ,x_{n})=CX={\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}}}$ се нарича средно хармонично.
  

(с други думи: средната хармонична стойност на числата е реципрочната на средната аритметична на техните реципрочни стойности)

• ${\displaystyle C_{2}(x_{1},\ldots ,x_{n})=CK={\sqrt {\frac {x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}}{n}}}}$ се нарича средноквадратично, известно също със съкращението RMS (на английски: Root mean square).
  

В статистическата практика се използват и средностепенни от трети и по-високи редове. Най-често срещаните от тях са средните кубични и средните биквадратични стойности:

• ${\displaystyle C_{3}(x_{1},\ldots ,x_{n})=CQ={\sqrt[{3}]{\frac {x_{1}^{3}+x_{2}^{3}+\cdots +x_{n}^{3}}{n}}}}$ се нарича среднокубично
• ${\displaystyle C_{4}(x_{1},\ldots ,x_{n})=CBK={\sqrt[{4}]{\frac {x_{1}^{4}+x_{2}^{4}+\cdots +x_{n}^{4}}{n}}}}$ се нарича среднобиквадратично

Минималното и максималното число от набор от положителни числа се изразяват като средните степени ${\displaystyle -\infty }$ и ${\displaystyle +\infty }$ на тези числа:

${\displaystyle \operatorname {min} \{x_{1},\ldots ,x_{n}\}=C_{-\infty }(x_{1},\ldots ,x_{n})=\lim _{s\to -\infty }C_{s}(x_{1},\dots ,x_{n});}$

${\displaystyle \operatorname {max} \{x_{1},\ldots ,x_{n}\}=C_{+\infty }(x_{1},\ldots ,x_{n})=\lim _{s\to \infty }C_{s}(x_{1},\dots ,x_{n}).}$

Свойства

За редицата от положителни реални числа ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ са валидни следните свойства: ^[4]

• Всяко средностепенно винаги се намира между най-малката и най-голямата стойност на ${\displaystyle x}$:

${\displaystyle \min(x_{1},\dots ,x_{n})\leq C_{s}(x_{1},\dots ,x_{n})\leq \max(x_{1},\dots ,x_{n})}$.

• Всяка средностепенна стойност е симетрична функция на своите аргументи; пермутирането на аргументите на средностепенното не променя неговата стойност:

${\displaystyle C_{s}(x_{1},\dots ,x_{n})=C_{s}(P(x_{1},\dots ,x_{n}))}$, където ${\displaystyle P}$ е пермутационен оператор.

• Като повечето средства, средностепенната стойност е хомогенна функция на своите аргументи ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$. Тоест, ако ${\displaystyle b}$ е положително реално число, тогава средностепенна стойност с показател ${\displaystyle s}$ на числата ${\displaystyle b\cdot x_{1},b\cdot x_{1},\dots ,b\cdot x_{n}}$ е равна на ${\displaystyle b}$ пъти средностепенното на числата ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$:

${\displaystyle C_{s}(bx_{1},\dots ,bx_{n})=b.C_{s}(x_{1},\dots ,x_{n}).}$

• Подобно на квазиаритметичните средни стойности, изчисляването на средностепенната стойност може да бъде разделено на изчисления на еднакви по размер подблокове. Това позволява използването на алгоритъм „разделяй и владей“ за изчисляване на средните стойности, когато е желателно:

${\displaystyle C_{s}(x_{1},\dots ,x_{n\cdot k})=C_{s}\left[C_{s}(x_{1},\dots ,x_{k}),C_{s}(x_{k+1},\dots ,x_{2\cdot k}),\dots ,C_{s}(x_{(n-1)\cdot k+1},\dots ,x_{n\cdot k})\right]}$.

Геометрично доказателство без думи, че при а=MN и b=MP:
max(a,b) > средно квадратично (QM) > средно аритметично (AM) >
средно геометрично (GM) >
средно хармонично (HM) > min(a,b) за две различни положителни числа a и b ^[5][6]

Обобщено неравенство на средните

Като цяло, ако ${\displaystyle s<q}$, тогава

${\displaystyle C_{s}(x_{1},\dots ,x_{n})\leq C_{q}(x_{1},\dots ,x_{n})}$

и двете средни са равни тогава и само тогава ако x₁ = x₂ = ... = x_n.

Неравенството е вярно за реални стойности на ${\displaystyle s}$ и ${\displaystyle q}$, както и за положителни и отрицателни стойности за безкрайност. То следва от факта, че за всички реални ${\displaystyle s}$,

${\displaystyle {\frac {\partial }{\partial s}}C_{s}(x_{1},\dots ,x_{n})\geq 0,}$

което може да се докаже с помощта на неравенството на Йенсен.

По-специално, за ${\displaystyle s}$ в {−1, 0, 1}, средностепенното предполага неравенството на Питагоровите средни (на украински: Піфагорові середні), както и неравенството на средните аритметични и геометрични:

${\displaystyle C_{-\infty }(x_{i})\leq C_{-1}(x_{i})\leq C_{1}(x_{i})\leq C_{2}(x_{i})\leq C_{3}(x_{i})\leq C_{4}(x_{i})\leq C_{\infty }(x_{i})}$, ${\displaystyle i=1,\dots ,n}$, или

${\displaystyle \min(x_{1},\ldots ,x_{n})\leq {\bar {x}}_{\mathrm {harm} }\leq {\bar {x}}_{\mathrm {geom} }\leq {\bar {x}}_{\mathrm {aritm} }\leq {\bar {x}}_{\mathrm {kvadr} }\leq {\bar {x}}_{\mathrm {qubich} }\leq {\bar {x}}_{\mathrm {bikv} }\leq \max(x_{1},\ldots ,x_{n}).}$