Eкстремум

Eкстремум (от латински: extremum – „краен“) в математиката е максималната или минималната стойност на функцията в дадено множество. Тази точка може да е бъде както локален екстремум, така и глобален екстремум.

Локален и глобален максимум и минимум на функцията cos(3πx)/x, 0.1≤ x ≤1.1

Определение

Ако е дадена функцията ${\displaystyle f\colon M\subset \mathbb {R} \to \mathbb {R} }$, за която ${\displaystyle x_{0}\in M^{0}}$, тогава:

• ${\displaystyle x_{0}}$ се нарича точка на локален максимум на функцията ${\displaystyle f,}$ ако съществува прекъсната част ${\displaystyle {\dot {U}}(x_{0})}$ такава, че

  ${\displaystyle \forall x\in {\dot {U}}(x_{0}):f(x)\leqslant f(x_{0})\;;}$

• ${\displaystyle x_{0}}$се нарича точка на локален минимум на функцията ${\displaystyle f,}$ ако съществува прекъсната част ${\displaystyle {\dot {U}}(x_{0})}$ такава, че

  ${\displaystyle \forall x\in {\dot {U}}(x_{0}):f(x)\geqslant f(x_{0})\;.}$

Определение за локален екстремум

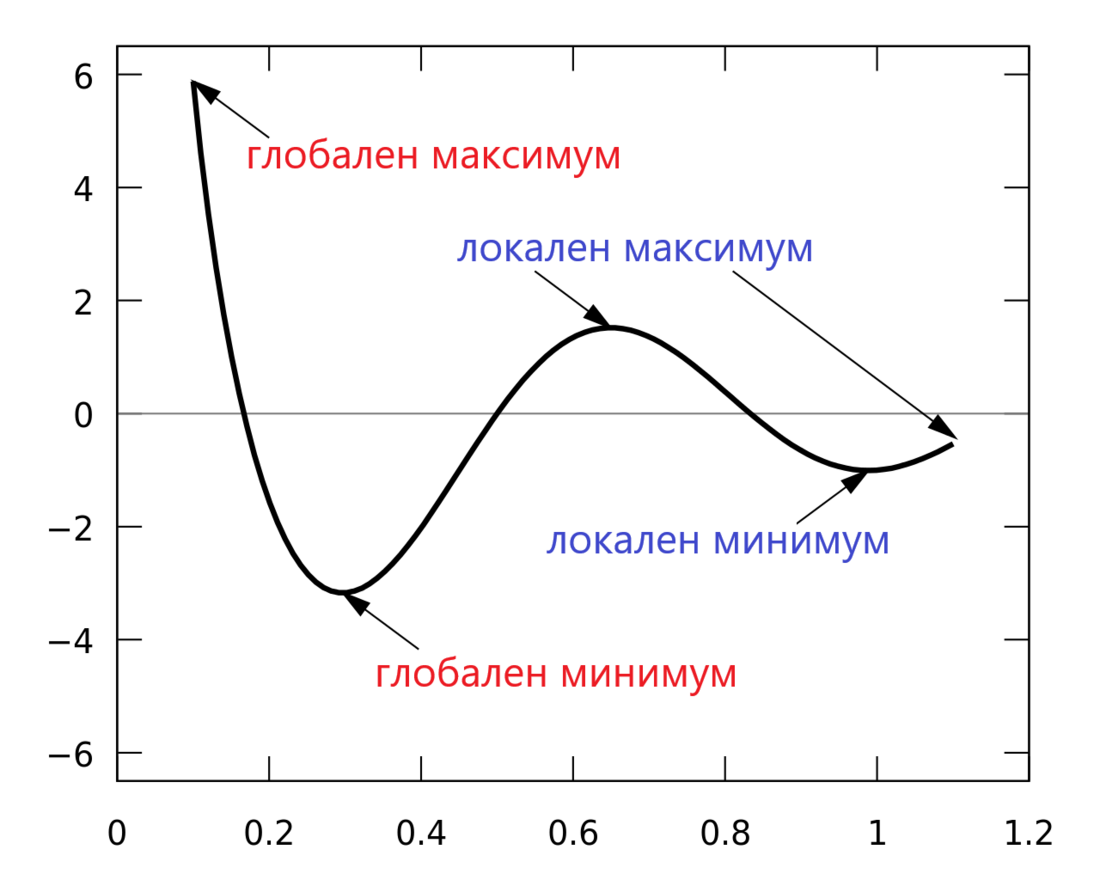
Ако дефиниционното множество на една функция е интервал, обикновено той може да се раздели на подинтервали, във всеки от който функцията е растяща или намаляваща. Сега да разгледаме поведението на функцията в точка, разделяща два съседни интервала, в които тя от растяща става намаляваща и обратното. В първия подинтервал на снимката функцията намалява, в следващия расте и т.н. Точките, където функцията от растяща става намаляваща и обратното са екстремуми. В достатъчно малка околност на тези точки няма други стойности на функцията, които да са съответно по-малки (по-големи, в когато става въпрос за максимум, а не за минимум) от стойността на функцията в тази точка.

Локален минимум

Функцията ${\displaystyle f(x)}$ има локален минимум в точка ${\displaystyle x=c}$ от дефиниционната си област, когато може да се намери достатъчно малка околност ${\displaystyle (c-\varepsilon ;c+\varepsilon )}$, с ${\displaystyle \varepsilon >0}$ от дефиниционната област на ${\displaystyle f}$, в която няма стойноси на ${\displaystyle f}$, по-малки от ${\displaystyle f(c)}$, т.е. $${\displaystyle f(x)\geqslant f(c)}$$ за ${\displaystyle x}$ принадлежащо на ${\displaystyle (c-\varepsilon ;c+\varepsilon )}$, с ${\displaystyle \varepsilon >0}$.

Локален максимум

Функцията ${\displaystyle f(x)}$ има локален максимум в точка ${\displaystyle x=c}$ от дефиниционната си област, когато може да се намери достатъчно малка околност ${\displaystyle (c-\varepsilon ;c+\varepsilon )}$, с ${\displaystyle \varepsilon >0}$ от дефиниционната област на ${\displaystyle f}$, в която няма стойности на ${\displaystyle f}$, по-големи от ${\displaystyle f(c)}$, т.е. $${\displaystyle f(x)\leqslant f(c)}$$ за ${\displaystyle x}$ принадлежащо на ${\displaystyle (c-\varepsilon ;c+\varepsilon )}$, с ${\displaystyle \varepsilon >0}$.

Необходимо условие за локален екстремум

Ако функцията ${\displaystyle f(x)}$ има екстремум в дадена точка и е диференцируема в тази точка, първата ѝ производна в тази точка е равна на нула.

Достатъчно условие за локален екстремум

Ако функцията ${\displaystyle f(x)}$ е два пъти диференцируема в околност на точката ${\displaystyle x=x_{0}}$, при което ${\displaystyle f'(x_{0})=0}$, а ${\displaystyle f''(x_{0})}$ е различно от ${\displaystyle 0}$, като ${\displaystyle f''(x)}$ е непрекъсната в тази точка, функцията има екстремум в точката x = x₀ – минимум, когато ${\displaystyle f''(x_{0})>0}$ и максимум, когато ${\displaystyle f''(x_{0})<0}$.

Източници

1. Учебник по математика за 12 клас, профилирана подготовка, издателство „Просвета“