শীর্ষ প্রশ্ন
সময়রেখা
চ্যাট
প্রসঙ্গ
ভর
মৌলিক রাশি উইকিপিডিয়া থেকে, বিনামূল্যে একটি বিশ্বকোষ
Remove ads
ভর হলো একটি বস্তুর অন্তর্নিহিত বৈশিষ্ট্য। পরমাণু এবং কণিকা পদার্থবিজ্ঞান আবিষ্কারের পূর্বে ধারণা করা হত যে, এটি বস্তুর মধ্যে থাকা পদার্থের পরিমাণের সাথে সম্পর্কিত। পরবর্তীতে দেখা গেছে, পরমাণু এবং মৌলিক কণাতে তাত্ত্বিকভাবে একই পরিমাণ পদার্থ থাকার পরেও, ভিন্ন ভিন্ন ভর ধারণ করে। আধুনিক পদার্থবিজ্ঞানে ভরের একাধিক সংজ্ঞা রয়েছে, যা ধারণাগতভাবে পৃথক হলেও শারীরিকভাবে সমতুল্য।[১] পরীক্ষামূলকভাবে ভরকে বস্তুর জড়তার পরিমাপ হিসেবে সংজ্ঞায়িত করা যেতে পারে, অর্থাৎ, একটি নিট বল প্রয়োগ করার সময় গতির পরিবর্তন (ত্বরণ) এর প্রতি যে প্রতিরোধ সৃষ্টি হয়।
ভরের এসআই একক হলো কিলোগ্রাম (কেজি)। পদার্থবিজ্ঞানে, ভর এবং ওজন দুটি আলাদা বিষয়। মহাকর্ষ বলের প্রভাবে একটি বস্তুর ওজন চাঁদে পৃথিবীর তুলনায় কম হবে, তবে এর ভর একই থাকবে। এটির কারণ ওজন হলো একপ্রকার বল, ভর এমন একটি বৈশিষ্ট্য যা (মহাকর্ষ সহ) এই বলের শক্তি নির্ধারণ করে।
পদার্থবিজ্ঞানের প্রমিত মডেল অনুযায়ী, মৌলিক কণার ভর ধারণা করা হয় যে, এটি হিগস বোজনের সাথে তাদের সংযোগের ফলস্বরূপ, যা ব্রাউট-এংলার্ট-হিগস প্রক্রিয়া হিসেবে পরিচিত।[২]
Remove ads
পরিমাপ
সারাংশ
প্রসঙ্গ
ভরের পরিমাপ করার জন্য বেশ কয়েকটি আলাদা পদ্ধতি রয়েছে। যদিও কিছু বিজ্ঞানী মনে করেছেন যে এই পদ্ধতি একে অপর থেকে স্বাধীন হতে পারে,[৩] তবে বর্তমান পরীক্ষা-নিরীক্ষাগুলি যে পদ্ধতিতেই এটি পরিমাপ করা হোক না কেন, ফলাফলে কোনো পার্থক্য খুঁজে পাওয়া যায় নি।
- জড়তার ভর একটি বস্তুর ত্বরণে প্রতিরোধ পরিমাপ করে, যখন সেই বস্তুর উপর কোন বল প্রয়োগ করা হয় (যা F = ma সম্পর্ক দ্বারা চিহ্নিত)।
- সক্রিয় মহাকর্ষীয় ভর একটি বস্তুর দ্বারা সৃষ্ট মহাকর্ষীয় ক্ষেত্রের শক্তি নির্ধারণ করে।
- নিষ্ক্রিয় মহাকর্ষীয় ভর একটি বস্তুর উপর একটি পরিচিত মহাকর্ষীয় ক্ষেত্রের প্রভাবে প্রয়োগিত মহাকর্ষীয় শক্তি পরিমাপ করে।
একটি বস্তুর ভর তার ত্বরণ নির্ধারণ করে যখন বল প্রয়োগ করা হয়। জড়তা এবং জড়তার ভর এই বাহ্যিক বৈশিষ্ট্যটি যথাক্রমে গুণগত এবং পরিমাণগত স্তরে বর্ণনা করে। নিউটনের গতির দ্বিতীয় সূত্র অনুসারে, যদি একটি নির্দিষ্ট ভর m বস্তুকে একটি একক বল F এর অধীনে রাখা হয়, তবে তার ত্বরণ হবে,
a = F/m
একটি বস্তুর ভর এটাও নির্ধারণ করে যে, এটি কতোটা শক্তিতে মহাকর্ষীয় ক্ষেত্র সৃষ্টি করে এবং কতটা প্রভাবিত হয়। যদি একটি প্রথম বস্তুর ভর mA দ্বিতীয় বস্তুর ভর mB থেকে r (ভর কেন্দ্র থেকে ভর কেন্দ্র) দূরত্বে স্থাপন করা হয়, তবে প্রতিটি বস্তু একটি আকর্ষণ বল,
Fg = GmAmB/r2 এর অধীনে থাকবে,
যেখানে,
G = ৬.৬৭×১০−১১ N⋅kg−2⋅m2
এটি হল "মহাকর্ষীয় ধ্রুবক"। এটিকে কখনও কখনও মহাকর্ষীয় ভর বলা হয়। ১৭ শতক থেকে চলমান পরীক্ষাগুলি প্রদর্শন করেছে যে, জড়তা এবং মহাকর্ষীয় ভর একে অপরের সমান; ১৯১৫ সাল থেকে, এই পর্যবেক্ষণটি সাধারণ আপেক্ষিকতার সমতার নীতিতে পূর্বধারণা হিসেবে অন্তর্ভুক্ত করা হয়েছে।
Remove ads
ভরের একক সমূহ
সারাংশ
প্রসঙ্গ
আন্তর্জাতিক একক পদ্ধতি (এসআই) অনুযায়ী ভরের একক হলো কিলোগ্রাম (কেজি)। এক কিলোগ্রাম ১০০০ গ্রাম এর সমান, এবং ১৭৯৫ সালে প্রথম এটি সংজ্ঞায়িত করা হয় একটি কিউবিক ডেসিমিটার পানির ভর হিসেবে যা বরফের গলনাঙ্কে ছিল। তবে, নির্দিষ্ট তাপমাত্রা এবং চাপের নিচে একটি কিউবিক ডেসিমিটার পানির সঠিক পরিমাপ করা কঠিন ছিল, তাই ১৮৮৯ সালে কিলোগ্রামকে একটি ধাতুর বস্তুর ভর হিসেবে পুনঃসংজ্ঞায়িত করা হয়, এবং এর ফলে এটি মিটার এবং পানির গুণাবলীর থেকে স্বাধীন হয়ে ওঠে। এই ধাতু বস্তুর মধ্যে ছিল ১৭৯৩ সালে তৈরি তামার প্রোটোটাইপ, ১৭৯৯ সালে প্লাটিনাম কিলোগ্রাম ডেস আর্কাইভস এবং ১৮৮৯ সালে প্লাটিনাম-ইরিডিয়াম আন্তর্জাতিক কিলোগ্রাম প্রোটোটাইপ (আইপিকে)।
এসআই ইউনিটের সাথে ব্যবহারের জন্য অনুমোদিত অন্যান্য ইউনিটগুলো হল:
- ১ টন (মেট্রিক টন) ১০০০ কেজির সমান।
- ইলেকট্রন ভোল্ট (eV), যা শক্তির একটি একক, ভরের পরিমাপ প্রকাশ করতে ব্যবহৃত হয় eV/c² এককে, ভর-শক্তির সমতুল্যতা মাধ্যমে।
- ডাল্টন (Da), যা একটি মুক্ত কার্বন-১২ পরমাণুর ভরের ১/১২ সমান, প্রায় 1.66×10⁻²⁷ কিলোগ্রাম।[ক]
এসআই ইউনিট ব্যতীত অন্যান্য ভরের অন্য ইউনিট গুলো হলো:
- পাউন্ড (lb), যা ভরের একটি একক (প্রায় ০.৪৫ কিলোগ্রাম), যা একই নামধারী পাউন্ড (বল) (প্রায় ৪.৫ নিউটন) এর সাথে ব্যবহৃত হয়, যা শক্তির একটি একক।[খ]
- সৌর ভর (M☉), যা সূর্যের ভর হিসেবে সংজ্ঞায়িত, প্রধানত জ্যোতির্বিজ্ঞানে ব্যবহৃত হয় বৃহৎ ভরের তুলনা করতে, যেমন তারা বা গ্যালাক্সি (≈ 1.99×10³⁰ কিলোগ্রাম)।
- একটি তারা বা কৃষ্ণগহ্বরের ভর, যা তার শোয়ার্জশিল্ড ব্যাসার্ধের সাথে সনাক্ত করা হয় (1 সেমি ≘ 6.73×10²⁴ কিলোগ্রাম)।
Remove ads
সংজ্ঞা
ভৌত বিজ্ঞানে, একজন ব্যক্তি ন্যূনতম সাতটি ভিন্ন ভিন্ন দৃষ্টিকোণ থেকে ভরের ধারণা আলাদা করতে পারে, বা সাতটি ভৌত ধারণা যা ভরের ধারণার সাথে সম্পর্কিত।[৪] এখন পর্যন্ত প্রতিটি পরীক্ষা দেখিয়েছে যে এই সাতটি মান পরস্পরানুপাতিক, এবং কিছু ক্ষেত্রে সমান, এবং এই পরস্পরানুপাতিকতা ভরের বিমূর্ত ধারণার উদ্ভব ঘটায়। ভর পরিমাপ বা কার্যকরভাবে সংজ্ঞায়িত করার বিভিন্ন পদ্ধতি রয়েছে:
- জড়তার ভর হল একটি বস্তুর ত্বরণ প্রতিরোধের পরিমাপ যখন বল প্রয়োগ করা হয়। এটি একটি বস্তুর উপর বল প্রয়োগ করে এবং সেই বল থেকে উদ্ভূত ত্বরণের পরিমাপ করে নির্ধারিত হয়। একটি ছোট জড়তার ভরের বস্তু একই বল দ্বারা প্রভাবিত হলে একটি বড় জড়তার ভরের বস্তুর চেয়ে বেশি ত্বরণ লাভ করবে। বলা হয় যে, বৃহত্তর ভরের বস্তুটির জড়তা বেশি।
- সক্রিয় মহাকর্ষীয় ভর হল একটি বস্তুর মহাকর্ষীয় প্রবাহের শক্তির পরিমাপ। মহাকর্ষীয় ক্ষেত্র পরিমাপ করা হয় একটি ছোট "বস্তু" কে মুক্তভাবে পড়তে দেয়ার মাধ্যমে এবং এর মুক্তপতনের ত্বরণ পরিমাপ করে। উদাহরণস্বরূপ, চাঁদের কাছে মুক্তপতনরত একটি বস্তু কম শক্তিশালী মহাকর্ষীয় ক্ষেত্রের প্রভাবের মধ্যে থাকে এবং সেই কারণে এটি ধীর গতিতে ত্বরণ লাভ করে, যা একই বস্তু পৃথিবীর কাছে মুক্তপতন করলে হত। চাঁদের কাছাকাছি মহাকর্ষীয় ক্ষেত্র দুর্বল কারণ চাঁদের সক্রিয় মহাকর্ষীয় ভর কম।[৫]
নিউটনের পূর্ববর্তী ধারণা
সারাংশ
প্রসঙ্গ
গ্যালিলিওর মুক্ত পতন ধারণা

১৬৩৮ সালের পূর্বে, গ্যালিলিও গ্যালিলেই তার দৃষ্টি নিবদ্ধ করেছিলেন মুক্ত পতনে থাকা বস্তুর উপর, তিনি বস্তুর গতির বৈশিষ্ট্য নির্ধারণের চেষ্টা করেছিলেন। গ্যালিলিও পৃথিবীর মহাকর্ষক্ষেত্রীয় গবেষণায় প্রথম ছিলেন না, এবং এর মৌলিক বৈশিষ্ট্যগুলি সঠিকভাবে বর্ণনাতেও তিনি প্রথম ছিলেন না, তবে শারীরিক নীতিগুলি প্রতিষ্ঠা করার জন্য বৈজ্ঞানিক পরীক্ষা-নিরীক্ষার উপর তার নির্ভরতা ভবিষ্যৎ প্রজন্মের বিজ্ঞানীদের উপর একটি গভীর প্রভাব ফেলেছিল। এটি অস্পষ্ট যে, এইগুলি কেবল ধারণাগত পরীক্ষা ছিল, যা একটি ধারণা ব্যাখ্যা করতে ব্যবহৃত হয়েছিল, নাকি গ্যালিলিও বাস্তব পরীক্ষা পরিচালনা করেছিলেন;[৬] তবে এই পরীক্ষা থেকে প্রাপ্ত ফলাফলগুলি বাস্তব এবং প্রাসঙ্গিক ছিল। গ্যালিলিওর শিষ্য ভিনচেনজো ভিভিয়ানির একটি জীবনী অনুযায়ী, গ্যালিলিও পিসার হেলে পড়া মিনার থেকে এক ধরনের পদার্থের কিন্তু ভিন্ন ভিন্ন ভরের বল ফেলেছিলেন, যাতে করে তিনি দেখাতে চেয়েছিলেন যে, তাদের পতনের সময় তাদের ভরের উপর নির্ভরশীল নয়। এই উপসংহারকে সমর্থন করতে, গ্যালিলিও নিম্নলিখিত তাত্ত্বিক যুক্তি উপস্থাপন করেছিলেন: তিনি প্রশ্ন করেছিলেন, যদি দুটি ভিন্ন ভরের এবং ভিন্ন পতনের গতির বস্তু একটি রশিতে বাঁধা থাকে, তবে কি অধিক ভর হওয়ার কারণে দ্রুত পতিত হবে, নাকি অপেক্ষাকৃত হালকা বস্তুটির ধীর পতন ভারী বস্তুটির পতনকে ধীর করে দেবে? এই প্রশ্নের একমাত্র যুক্তিসঙ্গত সমাধান হলো, সব বস্তু একই গতিতে পতিত হবে।[৭]
গ্যালিলিওর "Two New Sciences" গ্রন্থে ১৬৩৮ সালে বর্ণিত একটি পরবর্তী পরীক্ষার কথা উল্লেখ করা হয়েছে। গ্যালিলিওর একটি কাল্পনিক চরিত্র, সালভিয়াতি, একটি তামার বল এবং একটি কাঠের র্যাম্প ব্যবহার করে একটি পরীক্ষা বর্ণনা করেছেন। কাঠের র্যাম্পটি ছিল "১২ কিউবিট লম্বা, আধা কিউবিট চওড়া এবং তিন আঙুল পুরু", যার মধ্যে একটি সোজা, মসৃণ এবং পালিশ করা খাঁজ ছিল। খাঁজটি "প্যাপিরাসে আচ্ছাদিত ছিল, যা সম্ভবত সবচেয়ে মসৃণ এবং পালিশ করা ছিল"। এবং এই খাঁজে রাখা হয়েছিল "একটি কঠিন, মসৃণ এবং খুব গোল তামার বল"। র্যাম্পটি বিভিন্ন কোণে বাঁকানো হয়েছিল যাতে ত্বরণ ধীর করা যায়, যাতে সময়টি পরিমাপ করা যায়। বলটি র্যাম্পের উপর একটি পরিচিত দূরত্বে গড়িয়ে যেতে দেওয়া হয়েছিল, এবং ওই পরিচিত দূরত্বে বলটি পৌঁছাতে সময়টি পরিমাপ করা হয়েছিল।[৮]
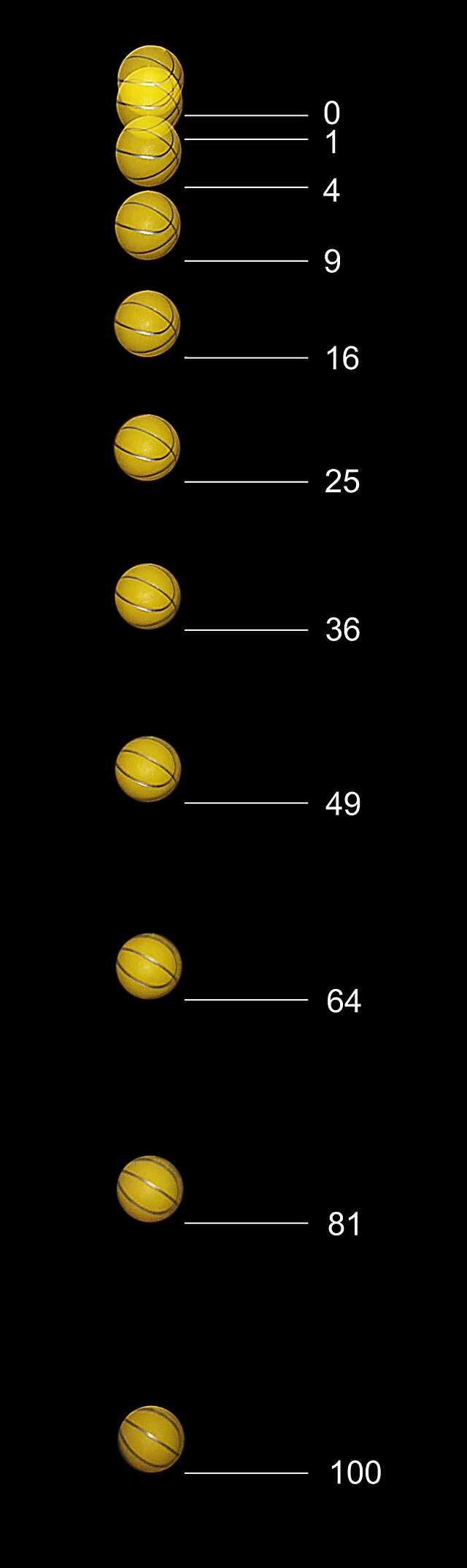
গ্যালিলিও এটি আবিষ্কার করেছিলেন যে, মুক্ত পতনে থাকা একটি বস্তুর জন্য, যে দূরত্বটি বস্তুটি পতিত হয়েছে তা সর্বদা ব্যবহৃত সময়ের বর্গের সাথে অনুপাতিক।
গ্যালিলিও প্রমাণ করেছিলেন যে, পৃথিবীর মহাকর্ষীয় ক্ষেত্রের প্রভাবে মুক্ত পতনে থাকা বস্তুর একটি ধ্রুব ত্বরণ থাকে, এবং গ্যালিলিওর সমসাময়িক, জোহানেস কেপলার প্রমাণ করেছিলেন যে, গ্রহগুলি সূর্যের মহাকর্ষীয় ভরের প্রভাবে উপবৃত্তাকার পথে চলমান। তবে, গ্যালিলিওর মুক্ত পতনগতির এবং কেপলারের গ্রহগতির মধ্যে গ্যালিলিওর জীবদ্দশায় পৃথকতা রয়ে গিয়েছিল।
ভর ও ওজনের পার্থক্য
কে. এম. ব্রাউনের মতে: "কেপলার একটি আলাদা ধারণা গঠন করেছিলেন ভরের (’পদার্থের পরিমাণ’), কিন্তু তিনি এটি ‘ওজন’ বলে অভিহিত করেছিলেন, যেমন তৎকালীন সকলেই করতেন।"[৯] অবশেষে, ১৬৮৬ সালে নিউটন এই আলাদা ধারণাটির নিজস্ব নাম দিলেন। 'প্রিন্সিপিয়া'র প্রথম অনুচ্ছেদে নিউটন পদার্থের পরিমাণকে “ঘনত্ব এবং আয়তন একত্রিতভাবে” হিসাবে সংজ্ঞায়িত করেছিলেন, এবং ভরকে পদার্থের পরিমাণ হিসাবে বর্ণনা করেছিলেন।[১০]
পদার্থের পরিমাণ হল তার পরিমাপ, যা তার ঘনত্ব এবং আয়তন একত্রিতভাবে উদ্ভূত হয়। ... এটি হল সেই পরিমাণ যা আমি পরবর্তী সময়ে সর্বত্র দেহ বা ভরের নামে উল্লেখ করব। এবং এটি প্রতিটি দেহের ওজন দ্বারা জানা যায়; কারণ এটি ওজনের সাথে অনুপাতিক।
Remove ads
নিউটনের ভর
সারাংশ
প্রসঙ্গ

রবার্ট হুক ১৬৭৪ সালে মহাকর্ষীয় শক্তির তার ধারণা প্রকাশ করেছিলেন, যেখানে তিনি বলেছিলেন যে সকল আকাশগঙ্গা বা সেলেস্টিয়াল বডির মধ্যে নিজস্ব কেন্দ্রের দিকে আকর্ষণ বা মহাকর্ষীয় শক্তি থাকে, এবং একইভাবে তারা তাদের কার্যকলাপের পরিসরে থাকা অন্যান্য জ্যোতির্বৈজ্ঞানিক বস্তুগুলোকেও আকর্ষণ করে। তিনি আরও উল্লেখ করেছিলেন যে, মহাকর্ষীয় আকর্ষণ বৃদ্ধি পায় যতটা নিকটবর্তী বস্তুর কেন্দ্রের কাছে পৌঁছায়।[১১] ১৬৭৯ ও ১৬৮০ সালে আইজ্যাক নিউটনের সাথে চিঠিপত্রের মাধ্যমে, হুক অনুমান করেছিলেন যে মহাকর্ষীয় শক্তি দুই বস্তুর মধ্যকার দুরত্বের দ্বিগুণ অনুযায়ী কমে যেতে পারে। হুক নিউটনকে উৎসাহিত করেছিলেন, যিনি ক্যালকুলাসের বিকাশে অগ্রণী ভূমিকা পালন করেছিলেন, যাতে তিনি কেপলারীয় কক্ষপথের গাণিতিক বিশদ বিবরণ তৈরি করে দেখতে পারেন যে হুকের অনুমান সঠিক ছিল কিনা। নিউটনের নিজস্ব অনুসন্ধান নিশ্চিত করে যে হুক সঠিক ছিলেন, কিন্তু ব্যক্তিগত পার্থক্যের কারণে নিউটন এটি হুকের কাছে প্রকাশ করেননি।
আইজ্যাক নিউটন তার আবিষ্কারগুলো সম্পর্কে চুপ ছিলেন ১৬৮৪ সাল পর্যন্ত, যখন তিনি তার বন্ধু এডমন্ড হ্যালিকে বলেছিলেন যে তিনি মহাকর্ষীয় কক্ষপথের সমস্যা সমাধান করেছেন, কিন্তু সমাধানটি তার অফিসে ভুলে রেখে এসেছিলেন। হ্যালির উৎসাহে নিউটন তার মহাকর্ষের ধারণাগুলি বিকাশ করতে এবং তার সমস্ত আবিষ্কার প্রকাশ করতে সিদ্ধান্ত নেন। নভেম্বর ১৬৮৪ সালে, নিউটন একটি নথি এডমন্ড হ্যালিকে পাঠান, যা এখন হারিয়ে গেছে তবে ধারণা করা হয় এর শিরোনাম ছিল "De motu corporum in gyrum"। হ্যালি নিউটনের আবিষ্কারগুলি রয়েল সোসাইটি অব লন্ডনে উপস্থাপন করেন, এবং একটি পূর্ণাঙ্গ উপস্থাপনার প্রতিশ্রুতি দেন। নিউটন পরে তার ধারণাগুলি একটি তিন খণ্ডের সেটে রেকর্ড করেন, যার নাম ছিল "ফিলোসফিয়া ন্যাচারালিস প্রিন্সিপিয়া ম্যাথামেটিকা"। প্রথম খণ্ডটি রয়েল সোসাইটিতে ১৬৮৫–৮৬ সালের ২৮ এপ্রিল গ্রহণ করা হয়; দ্বিতীয়টি ১৬৮৬–৮৭ সালের ২ মার্চ; এবং তৃতীয়টি ১৬৮৬–৮৭ সালের ৬ এপ্রিল। রোয়াল সোসাইটি নিউটনের পুরো সংগ্রহ তাদের নিজস্ব ব্যয়ে ১৬৮৬–৮৭ সালের মে মাসে প্রকাশ করে।[১২]
আইজ্যাক নিউটন কেপলার-এর মহাকর্ষীয় ভর এবং গ্যালিলিওর মহাকর্ষীয় ত্বরণ-এর মধ্যে ব্যবধান সৃষ্টি করেছিলেন, যার ফলস্বরূপ নিম্নলিখিত সম্পর্কটির উদ্ভাবন হয় যা উভয়কেই পরিচালিত করতঃ
যেখানে, হল একটি বস্তুর আপাত ত্বরণ, যা একটি এমন স্থানীয় অঞ্চলের মাধ্যমে চলে যেত যেখানে গুরত্বাকর্ষণ ক্ষেত্র বিদ্যমান, μ হল গুরত্বাকর্ষণীয় ভর (মানক গুরত্বাকর্ষণীয় প্যারামিটার) যা গুরত্বাকর্ষণ ক্ষেত্র সৃষ্টি করে, এবং হল রেডিয়াল কোঅর্ডিনেট (দুটি বস্তুর কেন্দ্রের মধ্যে দুরত্ব)। একটি বস্তুর মহাকর্ষণীয় ভর এবং তার মহাকর্ষণ ক্ষেত্রের মধ্যে সঠিক সম্পর্ক খুঁজে বের করে, নিউটন মহাকর্ষণীয় ভর পরিমাপ করার একটি দ্বিতীয় পদ্ধতি প্রদান করেছিলেন। পৃথিবীর ভর কেপলার পদ্ধতি ব্যবহার করে (পৃথিবীর চাঁদের কক্ষপথ থেকে) নির্ধারণ করা যেতে পারে, অথবা পৃথিবীর পৃষ্ঠে মহাকর্ষণীয় ত্বরণ পরিমাপ করে এবং সেটি পৃথিবীর ব্যাসের বর্গ দ্বারা গুণ করে সেটি নির্ধারণ করা যেতে পারে। পৃথিবীর ভর সূর্যের ভরের প্রায় তিন মিলিয়ন ভাগের এক ভাগ। এখন পর্যন্ত, মহাকর্ষণীয় ভর পরিমাপ করার অন্য কোনো সঠিক পদ্ধতি আবিষ্কার করা হয়নি।[১৩]
Remove ads
পারমাণবিক ভর
সাধারণত, বস্তুর ভর কিলোগ্রামের মাধ্যমে পরিমাপ করা হয়, যা ২০১৯ সাল থেকে প্রকৃতির মৌলিক ধ্রুবকগুলির ভিত্তিতে সংজ্ঞায়িত করা হয়েছে। একটি পরমাণু বা অন্য কণার ভর অন্য একটি পরমাণুর সাথে আরও সঠিকভাবে এবং আরও সুবিধাজনকভাবে তুলনা করা যেতে পারে, এবং এইভাবে বিজ্ঞানীরা ডাল্টন (যা একীভূত আণবিক ভর একক হিসাবেও পরিচিত) উন্নয়ন করেন। সংজ্ঞা অনুসারে, ১ ডা (একটি ডাল্টন) হল একটি কার্বন-১২ পরমাণুর ভরের ১/১২, এবং এইভাবে, একটি কার্বন-১২ পরমাণুর ভর একেবারে ১২ ডা।
Remove ads
টীকা
তথ্যসূত্র
বহিঃসংযোগ
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads



 ...
...

