অ্যালগরিদম

গণিত এবং কম্পিউটার বিজ্ঞানের আলোচনায় কলনবিধি বা ইংরেজি ভাষায় অ্যালগরিদম (Algorithm) বলতে একটি সুনির্দিষ্ট পদ্ধতিকে বোঝায়, যেটি কম্পিউটারে বাস্তবায়নযোগ্য ও সুনির্দিষ্ট ক্রমে বিন্যস্ত নির্দেশের সমষ্টি, যে নির্দেশগুলিকে ধাপগুলো অনুসরণ করে কোনও সুসংজ্ঞায়িত পরিগণনামূলক সমস্যার সমাধান করা হয়।^[১][২] অন্যভাবে বললে, কলনবিধি বা অ্যালগরিদম হচ্ছে ধাপে ধাপে সমস্যা সমাধানের পদ্ধতি বিশেষ। অর্থাৎ একটি সমস্যাকে সীমিত সংখ্যক কয়েকটি ধাপে ভেঙে প্রত্যেকটি ধাপ পরপর সমাধান করে সমগ্র সমস্যা সমাধান করা হয়। পরিগণক যন্ত্র (কম্পিউটার), রোবট, এমনকি মানুষও কলনবিধি বা অ্যালগরিদমের ধাপগুলি ধারাবাহিকভাবে অনুসরণ করে একটি নির্দিষ্ট কাজ সম্পাদন করতে পারে। পরিগণক বিজ্ঞানের (কম্পিউটার বিজ্ঞান) বিভিন্ন সমস্যা সমাধানের জন্য সঠিক কলনবিধি বা অ্যালগরিদমের ধারণাটি অত্যন্ত গুরুত্বপূর্ণ। কলনবিধি বা অ্যালগরিদমগুলি পরিগণনা (কম্পিউটেশন), উপাত্ত প্রক্রিয়াজাতকরণ (ডেটা প্রসেসিং), স্বয়ংক্রিয় যুক্তি, স্বয়ংক্রিয় সিদ্ধান্ত গ্রহণ এবং অন্যান্য কার্য সম্পাদনের জন্য বিনির্দেশ স্পেসিফিকেশন হিসেবে ব্যবহৃত হয়।

"নোট জি" থেকে অ্যাডা লাভলেসের ডায়াগ্রাম, প্রথম প্রকাশিত কম্পিউটার অ্যালগরিদম।

A এবং B নামক স্থানে দুটি সংখ্যার a এবং b-এর সর্বশ্রেষ্ঠ সাধারণ ভাজক(g.c.d) গণনার জন্য একটি অ্যালগরিদমের ফ্লোচার্ট (ইউক্লিডের অ্যালগরিদম )। অ্যালগরিদম দুটি লুপে ধারাবাহিক বিয়োগ দ্বারা এগিয়ে যায়: যদি পরীক্ষা B ≥ A "হ্যাঁ" দেয় বা "সত্য" (আরো সঠিকভাবে, B অবস্থানে থাকা সংখ্যাটি A অবস্থানে থাকা a সংখ্যাটির চেয়ে বড় বা সমান) তারপর, অ্যালগরিদম B ← B − A (অর্থাৎ সংখ্যা b − a পুরানো b প্রতিস্থাপন করে) নির্দিষ্ট করে। একইভাবে, IF A > B, তারপর A ← A − B। প্রক্রিয়াটি শেষ হয়ে যায় যখন (এর বিষয়বস্তু) B 0 হয়, g.c.d পাওয়া যায়। এ. (Scott 2009:13 থেকে প্রাপ্ত অ্যালগরিদম; Tausworthe 1977 থেকে চিহ্ন এবং অঙ্কন শৈলী)।

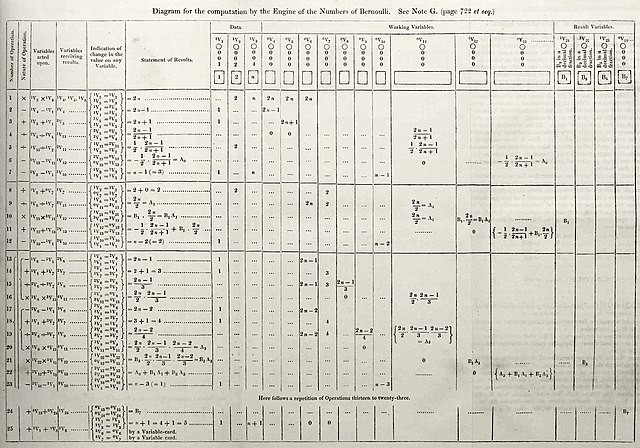
একটি কলনবিধি বা অ্যালগরিদমকে যেকোনও ভাষায় বর্ণনা করা যেতে পারে, সে ভাষাটি হতে পারে বাংলা, ইংরেজির মত মানুষের মৌখিক ভাষা,অথবা সি++ , এইচটিএমএল, এইচটিএমএল ৫, সিএসএস , পাইথন , সি , সি শার্প , গো , রুবি , জুলিয়া জাভার মত প্রোগ্রাম (পূর্বলিখিত নির্দেশক্রম) রচনার ভাষা। এমনকি যন্ত্রাংশসামগ্রী (হার্ডওয়্যার) নকশাকরণের মাধ্যমেও এটি বর্ণনা করা যেতে পারে। তবে যে ভাষাতেই লেখা হোক না, সমস্যা সমাধানের প্রতিটি ধাপের বর্ণনা কলনবিধি বা অ্যালগরিদমে থাকতে হবে।

পরিগণক বিজ্ঞান তথা কম্পিউটার বিজ্ঞানের সমস্ত ক্ষেত্রে যেমন উপাত্তাধার (ডেটাবেজ), চিত্রলিখন (গ্রাফিক্স), জালিকায়ন (কম্পিউটার নেটওয়ার্কিং), পরিচালক ব্যবস্থা (অপারেটিং সিস্টেম), কম্পিউটার নিরাপত্তা, কৃত্রিম বুদ্ধিমত্তা, ইত্যাদিতে কলনবিধি বা অ্যালগরিদম নির্মাণ ও বিশ্লেষণ একটি মৌলিক কর্মকাণ্ড। অ্যালগরিদম নির্মাণ এবং প্রোগ্রাম (পূর্বলিখিত নির্দেশক্রম) রচনার মধ্যে পার্থক্য আছে। কলনবিধি বা অ্যালগরিদম নির্মাণের সময় কোনও পরিগণনামূলক সমস্যা সমাধানের উদ্দেশ্যে লভ্য সমস্ত বিকল্প ঠিকমতো বোঝা অত্যাবশ্যক। অর্থাৎ কোনও নির্দিষ্ট সমাধানের জন্য কী যন্ত্রাংশসামগ্রী (হার্ডওয়্যার) ব্যবহৃত হবে, নেটওয়ার্ক তথা জালিকাব্যবস্থাটি কী রকম, কোন্‌ ভাষায় প্রোগ্রাম রচিত হবে, কর্মদক্ষতার উপরে কী কী সীমাবদ্ধতা বিদ্যমান, এই সব কিছু বিবেচনায় রাখতে হয়। কোনও অ্যালগরিদম যদি কোনও সমস্যাকে পূর্ণাঙ্গরূপে এবং দক্ষভাবে সমাধান করতে পারে, তাহলে সেটিকে "সঠিক" বিবেচনা করা হয়। অ্যালগরিদমগুলি প্রবিষ্ট উপাত্ত (ইনপুট) ও বহির্গত উপাত্তের (আউটপুট) মাধ্যমে কাজ করে। প্রবিষ্ট উপাত্তের উপরে কলনবিধি বা অ্যালগরিদমের প্রতিটি ধাপ ধারাবাহিকভাবে প্রয়োগ করা হয় এবং সবশেষে বহির্গত উপাত্ত ফলাফল হিসেবে প্রকাশিত হয়। একটি কলনবিধি বা অ্যালগরিদমকে তখনই "সঠিক" বলা হয় যদি প্রতিটি প্রবিষ্ট উপাত্তের জন্য কলনবিধি বা অ্যালগরিদমটি সঠিক বহির্গত উপাত্ত উৎপাদন করে। তবে পুরোপুরি নির্ভুল নয় এমন কলনবিধি বা অ্যালগরিদমও গুরুত্বপূর্ণ হতে পারে, যদি ভুলের মাত্রা নিয়ন্ত্রণের মধ্যে রাখা যায়।

ইংরেজি "অ্যালগরিদম" শব্দটি ৯ম শতাব্দীর মুসলিম গণিতবিদ মুসা আল খোয়ারিজমি-র নাম থেকে এসেছে।^{[৩][৪][৫]}

কলনবিধি বা অ্যালগরিদমের বিপরীত ধারণাটি হল আবিষ্করণী পদ্ধতি (Heuristic-হিউরিস্টিক), যা হল অতীত অভিজ্ঞতার মূল্যায়নের নিরিখে প্রয়াস ও প্রমাদের (trial and error) মধ্য দিয়ে আরোহী যুক্তিবিন্যাসের মাধ্যমে সমস্যা সমাধানের একটি পদ্ধতি; এটি সম্পূর্ণরূপে নির্দিষ্ট না-ও হতে পারে কিংবা সঠিক বা সর্বোত্তম ফলাফলের নিশ্চয়তা না-ও দিতে পারে (বিশেষ করে সেইসব সমস্যাক্ষেত্রে যেখানে কোন সুনির্দিষ্ট সঠিক বা সর্বোত্তম ফলাফল নেই)।^[৬]

ইতিহাস

অ্যালগরিদমের ইতিহাস: এক প্রাচীন যাত্রা

অ্যালগরিদমের ধারণা আদিকাল থেকেই বিদ্যমান। প্রাচীন ব্যাবিলনীয় গণিতবিদরা খ্রিস্টপূর্ব ২৫০০ সালেই পাটিগণিতমূলক অ্যালগরিদম—যেমন ভাগ করার পদ্ধতি—ব্যবহার করতেন। মিশরীয় গণিতবিদরাও খ্রিস্টপূর্ব ১৫৫০ সাল নাগাদ অনুরূপ পদ্ধতি প্রয়োগ করতেন। [১]

খ্রিস্টপূর্ব ২৪০ সালে, গ্রীক গণিতবিদরা মৌলিক সংখ্যা নির্ণয়ের জন্য ইরাটোস্থেনিসের চালুনি ও দুই সংখ্যার সর্বশ্রেষ্ঠ সাধারণ ভাজক নির্ণয়ের জন্য ইউক্লিডীয় অ্যালগরিদম ব্যবহার করেন। [২]

এরও বহু পরে, ৯ম শতকে, আরবি পণ্ডিত আল-কিন্দি ফ্রিকোয়েন্সি বিশ্লেষণের ভিত্তিতে কোড ভাঙার জন্য ক্রিপ্টোগ্রাফিক অ্যালগরিদম ব্যবহার করেন। [৩]

"অ্যালগরিদম" নামের উৎপত্তি

"Algorithm" শব্দটির উৎস ৯ম শতকের ফার্সি গণিতবিদ মুহাম্মদ ইবনে মুসা আল-খোয়ারিজমি—এর নাম থেকে, যার ল্যাটিন রূপ হয় Algoritmi। তিনি ছিলেন বাগদাদের হাউস অফ উইজডম-এর অন্যতম শ্রেষ্ঠ পণ্ডিত এবং হিন্দু-আরবি সংখ্যা পদ্ধতি ও বীজগণিতের ওপর প্রভাবশালী রচনার জন্য খ্যাত। তাঁর একটি পাণ্ডুলিপি, যা ১২শ শতকে ল্যাটিনে অনূদিত হয়, শুরু হয় "Dixit Algoritmi"—অর্থাৎ "এ কথা বলেছেন আল-খোয়ারিজমি"। [৪][৫][৬]

মধ্যযুগীয় ইউরোপে, "Algorismus" শব্দটি ধীরে ধীরে "decimal number system"-এর প্রতিশব্দে পরিণত হয়। পরবর্তীতে, গ্রিক শব্দ ἀριθμός (arithmos)—অর্থাৎ "সংখ্যা"—থেকে প্রভাবিত হয়ে শব্দটি হয়ে ওঠে Algorithmus, এবং অবশেষে ইংরেজি Algorithm শব্দটি গড়ে ওঠে, যার আধুনিক ব্যবহার শুরু হয় ১৯শ শতকে। [৯]

ভারতীয় ঐতিহ্যে অ্যালগরিদম

ভারতীয় গণিতচর্চা মূলত অ্যালগরিদমিক ছিল। শুলবাসূত্র থেকে শুরু করে কেরালা স্কুল পর্যন্ত নানা যুগে রচিত পাঠ্যে অ্যালগরিদম ছিল কেন্দ্রীয় উপাদান। এটি দেখায়, কেবল তত্ত্ব নয়, ব্যবহারিক সমস্যা সমাধানে সুসংগঠিত ধাপগত পদ্ধতি ভারতীয় জ্ঞানচর্চার শিকড়ে ছিল। [তথ্যসূত্র প্রয়োজন]

ইউরোপে শব্দটির আগমন

ইংরেজিতে "algorithm" শব্দটির প্রথম ব্যবহার পাওয়া যায় ১২৩০ সালে এবং পরবর্তীতে জিওফ্রে চসার ১৩৯১ সালে এটি ব্যবহার করেন। ১২৪০ সালের এক বিখ্যাত ল্যাটিন কবিতা Carmen de Algorismo, যেটি অ্যালেকজান্দ্রে দে ভিলেদিউ রচনা করেন, তাতে বলা হয়:

“This present art, in which we use those twice five Indian figures, is called Algorismus.”

অর্থাৎ: "এই শিল্প, যেখানে আমরা সেই দ্বিগুণ পাঁচটি ভারতীয় অঙ্ক ব্যবহার করি, তাকে অ্যালগোরিসমাস বলা হয়।" [১১]

আধুনিক অ্যালগরিদমের পথচলা

অ্যালগরিদমের আধুনিক সংজ্ঞার দিকে যাত্রা শুরু হয় ১৯২৮ সালে, যখন ডেভিড হিলবার্ট তাঁর বিখ্যাত Entscheidungsproblem (সিদ্ধান্ত সমস্যা) উত্থাপন করেন। এরপর একে একে আবির্ভূত হয়:

• গ্যোডেল–হারব্র্যান্ড–ক্লীনি-এর রিকার্সিভ ফাংশন (১৯৩০–৩৫),
• অ্যালনজো চার্চ-এর ল্যাম্বডা ক্যালকুলাস (১৯৩৬),
• এমিল পোস্ট-এর ফর্মুলেশন (১৯৩৬),
• এবং সর্বোপরি অ্যালান টুরিং-এর টুরিং মেশিন (১৯৩৬–৩৭), যা আধুনিক কম্পিউটেশনের ভিত্তি গড়ে তোলে। [১২][১৩]

অনানুষ্ঠানিক সংজ্ঞা

a detailed presentation of the various points of view on the definition of "algorithm" জন্য Algorithm characterizations দেখুন।

একটি ফ্লোচার্ট

অ্যালগরিদমের অনানুষ্ঠানিক সংজ্ঞা ও প্রয়োগ

অ্যালগরিদম বলতে সাধারণভাবে বোঝায় এমন একটি নিয়মতান্ত্রিক নির্দেশনার সেট, যা নির্দিষ্টভাবে কোনো কাজের ধাপক্রম নির্ধারণ করে। এটি কোনো গাণিতিক গণনা হতে পারে, আবার হতে পারে রান্নার রেসিপি বা আমলাতান্ত্রিক কোনো প্রক্রিয়াও। [১][২][৩]

একটি প্রোগ্রাম শুধুমাত্র তখনই "অ্যালগরিদম" হিসেবে গণ্য হয় যখন তা নির্দিষ্ট সময়ে থেমে যায়—অর্থাৎ, এটি সমাপ্তিযোগ্য। যদিও কিছু ক্ষেত্রে অসীম লুপ কাঙ্ক্ষিত হতে পারে, যেমন সার্ভার মনিটরিং বা রিয়েল-টাইম সিগন্যাল প্রসেসিংয়ে। [৪]

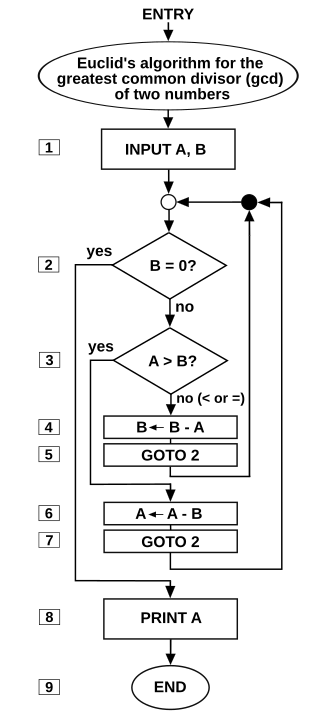
একটি ক্লাসিক উদাহরণ হল ইউক্লিডীয় অ্যালগরিদম, যা দুটি সংখ্যার সর্বোচ্চ সাধারণ ভাজক (GCD) নির্ধারণে ব্যবহৃত হয়। এটি ফ্লোচার্ট আকারেও উপস্থাপন করা যায়, যা পরবর্তী অংশে বর্ণিত।

---

বুলোস ও জেফ্রির দৃষ্টিভঙ্গি

Boulos & Jeffrey (1974, 1999) অ্যালগরিদমকে এমনভাবে ব্যাখ্যা করেন:^[৭]

“কোনো মানুষই যথেষ্ট দ্রুত বা যথেষ্ট ছোট লিখতে পারে না অসীম সেটের সব সদস্য একে একে তালিকাভুক্ত করতে। তবে তারা কিছু নির্দিষ্ট অসীম সেটের জন্য এমন নির্দেশনা দিতে পারে, যা অনুযায়ী যেকোনো নির্দিষ্ট n-এর জন্য সেটের n-তম সদস্য নির্ধারণ করা সম্ভব।”

এই "নির্দেশনাগুলি" এতটাই স্পষ্ট ও কাঠামোবদ্ধ হওয়া উচিত যাতে একটি কম্পিউটিং মেশিন, অথবা একটি মানুষ যার গাণিতিক জ্ঞান মৌলিক পর্যায়ের, তা অনুসরণ করতে পারে। [৫]^[১]

এখানে যে “সংখ্যাযোগ্য অসীম সেট”-এর কথা বলা হচ্ছে, তা হলো এমন একটি সেট যার উপাদানসমূহকে প্রাকৃতিক সংখ্যার (১, ২, ৩, ...) সঙ্গে এক-একটি চিঠিপত্রে ফেলা যায়।

উদাহরণস্বরূপ, একটি সরল অ্যালগরিদম হতে পারে:

y = m + n

যেখানে m ও n ইনপুট ভেরিয়েবল এবং y হলো আউটপুট।

তবে, “অ্যালগরিদম” শব্দটি শুধু এমন সহজ যোগফল বোঝায় না। বিভিন্ন লেখক একে বোঝাতে চেয়েছেন:^[৩]

• দ্রুত, দক্ষ এবং সুনির্দিষ্ট নির্দেশনা, যা কম্পিউটার বা যেকোনো "প্রক্রিয়াকরণকারী সত্তা" (মানুষ, যন্ত্র, অথবা যান্ত্রিক-বৈদ্যুতিক সিস্টেম) বুঝতে ও অনুসরণ করতে পারে। [৬][৭]
• যেভাবে প্রতীক (যেমন +, =) ও ইনপুট মান (যেমন m, n) থেকে কার্যকরভাবে আউটপুট তৈরি করা যায় নির্দিষ্ট নিয়ম মেনে এবং উপযুক্ত সময়ে। [৮][৯][১০]

---

নির্ধারকতা ও সিদ্ধান্তযোগ্যতা

অ্যালগরিদমের ধারণা যুক্তি ও সিদ্ধান্তযোগ্যতার সাথে গভীরভাবে সম্পর্কযুক্ত। একে বলা যেতে পারে “ফর্মাল সিস্টেম নির্মাণের কঙ্কাল”, যেখানে কিছু স্বতঃসিদ্ধ এবং নিয়ম থেকে পুরো গঠন তৈরি হয়।^[২]

তবে অ্যালগরিদমের কাজ শেষ হতে কত সময় লাগে—তা একে একাধিক মাত্রায় অনিশ্চিত করে তোলে। কারণ এটি শুধু সময়ের একক নয়, বরং কম্পিউটেশনাল ধাপের কাঠামোতে পরিমাপযোগ্য, যা আবার বাস্তব জগতের সময়-ধারণার সঙ্গে সরাসরি সম্পর্কযুক্ত নয়।^[৬]

---

প্রয়োগের ক্ষেত্র

অধিকাংশ অ্যালগরিদম তৈরি হয় কম্পিউটার প্রোগ্রামে প্রয়োগের জন্য। তবে অ্যালগরিদম:

• জৈবিক নিউরাল নেটওয়ার্ক (যেমন, মানব মস্তিষ্ক কীভাবে গণনা করে),
• বৈদ্যুতিক সার্কিট, কিংবা
• যান্ত্রিক যন্ত্র—এও বাস্তবায়িত হতে পারে।

উদাহরণস্বরূপ, একটি পোকাও খাদ্যের সন্ধানে প্রাকৃতিকভাবে একটি এলগরিদমিক প্যাটার্ন অনুসরণ করে।

আনুষ্ঠানিকতা

কম্পিউটার, অ্যালগরিদম এবং টুরিং মেশিন: একটি পর্যালোচনা

কম্পিউটার যেভাবে ডেটা প্রক্রিয়াকরণ করে, সেখানে অ্যালগরিদম অপরিহার্য ভূমিকা পালন করে। বেশিরভাগ কম্পিউটার প্রোগ্রামে এমন অ্যালগরিদম থাকে যা নির্দিষ্ট একটি কাজ সম্পাদনের জন্য ধাপে ধাপে নির্দেশনা দেয়। যেমন—কর্মচারীদের বেতন চেক গণনা বা ছাত্রদের রিপোর্ট কার্ড তৈরি। এসব কাজের পেছনে থাকে একগুচ্ছ নির্ভুল ও কাঠামোবদ্ধ নির্দেশনা, যা কম্পিউটারের বোঝার ও সম্পাদনের উপযোগী।

এইভাবে, একটি অ্যালগরিদমকে ধরা যেতে পারে এমন ধাপভিত্তিক কার্যপ্রবাহ হিসেবে যা একটি টুরিং-সম্পূর্ণ সিস্টেম দ্বারা অনুকরণযোগ্য। মিনস্কি (1967), স্যাভেজ (1987), ও গুরেভিচ (2000) এ ধরনের দাবির পক্ষে তর্ক করেছেন।

মিনস্কি বলেন:

“আমরা টুরিংয়ের মতো করেই ধরে নিতে পারি, যেকোনো পদ্ধতি যা ‘স্বাভাবিকভাবে কার্যকর’—তা আসলে একটি সরল যন্ত্রের মাধ্যমেও বাস্তবায়নযোগ্য।” [১]

গুরেভিচ যুক্ত করেন:

“টুরিংয়ের যুক্তিগুলো এমন একটি শক্তিশালী ধারণাকে সমর্থন করে—যে প্রতিটি অ্যালগরিদমই একটি টুরিং মেশিন দ্বারা অনুকরণযোগ্য।”

স্যাভেজ (1987) মত দেন:

“একটি অ্যালগরিদম মানে একটি টুরিং মেশিন দ্বারা সংজ্ঞায়িত গণনামূলক প্রক্রিয়া।” [২]

---

থামা ও থামানো সমস্যা

টুরিং মেশিন এমন অনেক গণনামূলক প্রক্রিয়া সংজ্ঞায়িত করতে পারে, যেগুলো কখনো থামে না। কিন্তু অ্যালগরিদমের অনানুষ্ঠানিক সংজ্ঞায় সাধারণত এই “সমাপ্তিযোগিতা” একটি অপরিহার্য শর্ত। এই প্রয়োজনীয়তা থেকেই উঠে আসে “থামানো সমস্যা” (Halting Problem)—কম্পিউটেবিলিটি তত্ত্বের একটি মূল উপপাদ্য। এটি প্রমাণ করে, একটি সাধারণ পদ্ধতিতে বোঝা সম্ভব নয় যে একটি অ্যালগরিদম সবসময় থামবে কি না।

---

তথ্য প্রক্রিয়াকরণ ও অভ্যন্তরীণ অবস্থা

যখন একটি অ্যালগরিদম তথ্য প্রক্রিয়াকরণের সঙ্গে যুক্ত থাকে, তখন তা:

• ইনপুট-এর মাধ্যমে তথ্য পড়ে,
• আউটপুট-এ ফলাফল লিখে,
• এবং স্টোরেজে সেই তথ্য ভবিষ্যৎ প্রক্রিয়ার জন্য সংরক্ষণ করে।

এই সঞ্চিত তথ্যই মূলত অ্যালগরিদম সম্পাদনকারী সত্তার অভ্যন্তরীণ অবস্থা (state)। সাধারণত এটি এক বা একাধিক ডেটা স্ট্রাকচার-এ সংরক্ষিত থাকে।

---

নির্ভুলতা ও শর্তসাপেক্ষ পদক্ষেপ

বেশ কিছু গণনামূলক প্রক্রিয়ায়, অ্যালগরিদমকে অত্যন্ত কঠোরভাবে সংজ্ঞায়িত করতে হয়। এর মানে, প্রতিটি সম্ভাব্য পরিস্থিতির জন্য কীভাবে কাজ করবে তা সুস্পষ্টভাবে নির্ধারণ করতে হয়। শর্তসাপেক্ষ পদক্ষেপগুলো (যেমন if, else) এমনভাবে গঠন করতে হয় যাতে প্রতিটি কেসের মানদণ্ড পরিষ্কার এবং গণনাযোগ্য হয়।

---

নির্দেশনার ধারা ও নিয়ন্ত্রণের প্রবাহ

অ্যালগরিদম হলো একটি সুনির্দিষ্ট নির্দেশনার তালিকা, যেটি নির্দিষ্ট একটি ক্রমে অনুসরণ করা হয়। এই নির্দেশনাগুলি সাধারণত:

• “উপরে থেকে নিচে” তালিকাভুক্ত থাকে,
• এবং একটি সুসংগঠিত নিয়ন্ত্রণ প্রবাহ (control flow) অনুসরণ করে।

এই নিয়ন্ত্রিত প্রবাহের মাধ্যমে প্রতিটি ধাপ ঠিক কবে এবং কীভাবে সম্পাদিত হবে, তা নির্ধারিত হয়।

---

আনুষ্ঠানিক অ্যালগরিদম ও অ্যাসাইনমেন্ট অপারেশন

অ্যালগরিদমের আনুষ্ঠানিককরণের কেন্দ্রীয় ধারণা হলো "যান্ত্রিক কার্যকারিতা"—একটি নির্দিষ্ট কাজকে এমনভাবে ভেঙে ফেলা, যাতে কম্পিউটার তা অনায়াসে সম্পাদন করতে পারে।

এই প্রেক্ষিতে, একটি গুরুত্বপূর্ণ গঠনমূলক উপাদান হলো assignment operation—যার মাধ্যমে একটি ভেরিয়েবলকে নির্দিষ্ট মান প্রদান করা হয়। এটি সেই ধারণা থেকে আসে যে কম্পিউটার একটি “স্ক্র্যাচপ্যাড” মেমোরি ব্যবহার করে প্রতিটি ধাপ ধরে রাখতে পারে।

উদাহরণস্বরূপ:

---

অ্যালগরিদমের বিকল্প গঠন

যদিও আমরা এখানে imperative (আদেশমূলক) প্রোগ্রামিং ধারায় অ্যালগরিদম বিশ্লেষণ করেছি, তবে বিকল্প দৃষ্টিভঙ্গিও রয়েছে:

• Functional Programming: যেখানে অ্যালগরিদম গঠিত হয় ফাংশনের মাধ্যমে।
• Logic Programming: যেখানে সমস্যার সমাধান হয় নিয়ম ও তথ্যভাণ্ডারের ভিত্তিতে।

অ্যালগরিদম প্রকাশ করা

অ্যালগরিদম: বহুরূপী ভাষার এক সুসংহত প্রকাশ

অ্যালগরিদম একটি বিমূর্ত ধারণা হলেও, তার প্রকাশ বহুরূপে ঘটে—বিভিন্ন স্বরলিপি ও ভাষায়। এর রূপায়ণ ঘটে নিচের মাধ্যমগুলোতে:

• প্রাকৃতিক ভাষা (Natural Language)
• সিউডোকোড (Pseudocode)
• ফ্লোচার্ট (Flowchart)
• ড্রাকন-চার্ট (DRACON chart)
• প্রোগ্রামিং ভাষা
• নিয়ন্ত্রণ টেবিল (Control tables) – যা দোভাষীদের মাধ্যমে প্রক্রিয়াকৃত হয়

প্রাকৃতিক ভাষা

প্রাকৃতিক ভাষায় অ্যালগরিদম ব্যাখ্যা করা গেলেও, তা সাধারণত অস্পষ্টতা ও ভিন্নার্থের ঝুঁকিতে থাকে। সেজন্য জটিল বা প্রযুক্তিগত অ্যালগরিদমে এটি খুব কম ব্যবহৃত হয়।

সিউডোকোড, ফ্লোচার্ট, ড্রাকন-চার্ট

এগুলো হল গঠনমূলক ও কাঠামোবদ্ধ উপস্থাপনাপদ্ধতি, যা প্রাকৃতিক ভাষার অস্পষ্টতা এড়িয়ে নির্ভুলভাবে অ্যালগরিদমকে উপস্থাপন করে। পাঠক, প্রোগ্রামার ও পরিকল্পনাকারীরা সহজে এগুলো থেকে প্রক্রিয়াটি অনুধাবন করতে পারে।

প্রোগ্রামিং ভাষা

প্রোগ্রামিং ভাষার মূল উদ্দেশ্য অ্যালগরিদমকে এমনভাবে উপস্থাপন করা, যাতে একটি কম্পিউটার কার্যকরভাবে সেটি সম্পাদন করতে পারে। একইসঙ্গে, এগুলো নথিভুক্তি ও ব্যাখ্যার মাধ্যম হিসেবেও ব্যবহৃত হয়।

---

বিকল্প উপস্থাপনা: যান্ত্রিক রূপে চিন্তার ছায়া

একই অ্যালগরিদমকে ভিন্ন ভিন্নভাবে প্রকাশ করা সম্ভব, যেমন:

• একটি টিউরিং মেশিন প্রোগ্রামকে রূপান্তর করা যায় মেশিন টেবিলের ক্রম হিসেবে (দেখুন: সীমিত-রাষ্ট্র মেশিন, ট্রানজিশন টেবিল)
• অথবা, স্টেট ডায়াগ্রাম, ফ্লোচার্ট বা ড্রাকন-চার্ট হিসেবে
• এমনকি, প্রাথমিক মেশিন কোড বা অ্যাসেম্বলি ভাষাতেও প্রকাশ করা যায়, যাকে বলা হয় “চতুষ্পদগুলির সেট” (quadruples)

---

টিউরিং মেশিনের তিন স্তরের উপস্থাপনা

একটি অ্যালগরিদমকে টিউরিং মেশিন ভাষায় প্রকাশ করা যায় তিনটি স্বীকৃত স্তরে:

১. উচ্চ-স্তরের বর্ণনা (High-level description)

এই স্তরে অ্যালগরিদমকে গদ্যে ব্যাখ্যা করা হয়, মেশিন কীভাবে কাজ করে—তা উপেক্ষা করে। উদাহরণস্বরূপ:

“দুটি সংখ্যা যোগ করো এবং ফলাফল রিটার্ন করো।”

২. বাস্তবায়নের বিবরণ (Implementation description)

এখানে ব্যাখ্যা করা হয় টিউরিং মেশিন কীভাবে টেপ ও হেড পরিচালনা করে, কিন্তু এখনও রাজ্য বা রূপান্তরের সম্পূর্ণ টেবিল দেওয়া হয় না। এটি হলো মধ্যম স্তরের ব্যাখ্যা।

৩. আনুষ্ঠানিক বিবরণ (Formal description)

সবচেয়ে বিস্তারিত স্তর—স্টেট ট্রানজিশন টেবিল সহ সম্পূর্ণ গঠন তুলে ধরা হয়। এটি "মেশিন লেভেল"-এর বর্ণনা, যেখানে প্রতিটি ধাপ কঠোরভাবে নির্ধারিত।

---

একটি সরল উদাহরণ

এই তিনটি স্তরে একই কাজ—যেমন m + n যোগফল নির্ণয়—তিনভাবে তুলে ধরা যেতে পারে:

1. উচ্চ স্তর: "m ও n যোগ করে ফলাফল দাও।"
2. বাস্তবায়ন স্তর: "প্রথম সংখ্যাটি টেপে রেখে, এরপর দ্বিতীয়টি টেপে রেখে, হেড ডানদিকে সরাও..."
3. আনুষ্ঠানিক স্তর: একটি পূর্ণাঙ্গ ট্রানজিশন টেবিল, যেখানে প্রতিটি ইনপুট ও স্টেট অনুযায়ী হেডের গতি ও টেপের মান নির্ধারণ করা আছে।

ডিজাইন

1. অ্যালগরিদম ডিজাইন: সমস্যা সমাধানের গাণিতিক শিল্প

অ্যালগরিদম ডিজাইন বলতে বোঝানো হয় একটি পদ্ধতিগত বা গাণিতিক প্রক্রিয়া, যার মাধ্যমে আমরা জটিল কোনো সমস্যার সমাধান খুঁজি এবং কার্যকর অ্যালগরিদম নির্মাণ করি।

এটি কেবল কোড লেখা নয়—এ হলো চিন্তার স্থাপত্য, যেখানে প্রতিটি ধাপের পেছনে যুক্তির স্তম্ভ গাঁথা।

---

ডিজাইনের ভিত্তি: তত্ত্ব ও কৌশল

অ্যালগরিদম ডিজাইন অনেকাংশে অপারেশনস রিসার্চ, গাণিতিক মডেলিং এবং কম্পিউটার বিজ্ঞানের বিভিন্ন সমাধানমূলক কৌশলের উপর ভিত্তি করে গঠিত। এর মধ্যে বিশেষভাবে ব্যবহৃত হয়:

• ডায়নামিক প্রোগ্রামিং (Dynamic Programming)
• ডিভাইড-এন্ড-কনকার (Divide and Conquer)
• গ্রিডি অ্যালগরিদম (Greedy Algorithms)
• ব্যাকট্র্যাকিং, ব্রাঞ্চ অ্যান্ড বাউন্ড, প্রভৃতি

এসব কৌশলকে অনেক সময় বলা হয় অ্যালগরিদম ডিজাইন প্যাটার্ন, ঠিক যেমন সফটওয়্যার ইঞ্জিনিয়ারিং-এ টেমপ্লেট মেথড বা ডেকোরেটর প্যাটার্ন ব্যবহৃত হয়।

---

দক্ষতা: শুধু সমাধান নয়, ভালো সমাধান

ডিজাইনের সবচেয়ে গুরুত্বপূর্ণ বিষয়গুলোর একটি হলো দক্ষতা—অর্থাৎ অ্যালগরিদমটি কত দ্রুত চলে এবং কতটা মেমরি ব্যবহার করে।

এর জন্য আমরা ব্যবহার করি বিগ-ও নোটেশন (Big-O notation), যা একটি অ্যালগরিদমের রানটাইম বা মেমোরি ব্যবহারের বৃদ্ধি বর্ণনা করে ইনপুট সাইজ বৃদ্ধির সঙ্গে।

উদাহরণস্বরূপ:

• O(1) – স্থির সময়
• O(n) – ইনপুটের সঙ্গে সরলরেখায় বাড়ে
• O(n log n) – দক্ষ এবং গঠনমূলক
• O(n²) বা তার বেশি – খরচসাপেক্ষ, বড় ইনপুটে ধীরগতি

---

অ্যালগরিদম নির্মাণের ধাপসমূহ

একটি কার্যকর অ্যালগরিদম গঠনের পেছনে থাকে একটি সুনির্দিষ্ট প্রক্রিয়া, যা সাধারণত নিচের ধাপগুলো অনুসরণ করে:

1. সমস্যার সংজ্ঞা নির্ধারণ – সমস্যাটি ঠিক কী? ইনপুট-আউটপুট কী হতে পারে?
2. একটি মডেল তৈরি – সমস্যাটি কীভাবে গাণিতিক বা লজিক্যালভাবে উপস্থাপন করা যায়?
3. অ্যালগরিদমের স্পেসিফিকেশন – প্রত্যাশিত ধাপসমূহ কী হবে? শর্তাবলি কী?
4. ডিজাইন কৌশল প্রয়োগ – ডায়নামিক প্রোগ্রামিং? না গ্রিডি?
5. সঠিকতা যাচাই – অ্যালগরিদম সত্যিই কাজ করে তো?
6. পারফরম্যান্স বিশ্লেষণ – কত দ্রুত? কতটা স্থানের দরকার?
7. বাস্তবায়ন (Implementation) – পছন্দের প্রোগ্রামিং ভাষায় কোডিং
8. পরীক্ষা (Testing) – বিভিন্ন ইনপুট দিয়ে ফলাফল যাচাই
9. ডকুমেন্টেশন প্রস্তুতি – যেন অন্যরাও বুঝতে পারে, প্রয়োজনে পরিমার্জন করতে পারে

(NB: কিছু ধাপের গভীরতা বা ক্রম প্রকল্পভেদে ভিন্ন হতে পারে)

আরও দেখুন

• গণিত প্রবেশদ্বার

• অ্যালগল
• বিমূর্ত পরিগণক যন্ত্র
• পরিগণনামূলক জটিলতা তত্ত্ব
• পরিগণনীয়তা তত্ত্ব

কম্পিউটার অ্যালগরিদম

লজিক্যাল NAND অ্যালগরিদম 7400 চিপে ইলেকট্রনিকভাবে প্রয়োগ করা হয়েছে