Espai revestiment

En topologia, un espai revestiment és una tripleta ${\displaystyle [{\tilde {X}},p,X]}$ on ${\displaystyle {\tilde {X}},X}$ són espais topològics i ${\displaystyle p:{\tilde {X}}\to X}$ és una funció contínua i suprajectiva

Y és un revestiment de X

A més es compleix que ${\displaystyle \forall x\in X\quad \exists U}$ oberta En ${\displaystyle X}$ veïnatge de ${\displaystyle x}$ tal que

${\displaystyle p^{-1}U=\bigcup _{j}{\tilde {U}}_{j}}$

on per a cada ${\displaystyle {\tilde {U}}_{j}}$ l'map ${\displaystyle p|_{{\tilde {U}}_{j}}:{\tilde {U}}_{j}\to U}$ és un Homeomorfisme.

El concepte d'espai revestiment s'utilitza en ciències com ara la geometria diferencial, els grups de Lie, superfícies de Riemann, Homotopia, teoria de nusos.

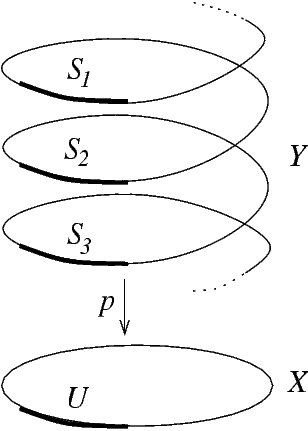
L'exemple prototip és ${\displaystyle \mathbb {R} \to S^{1}}$ donat per ${\displaystyle t\mapsto i^{it}}$.

Revestiment universal

Entre tots els espais revestiment d'un espai ${\displaystyle X\,}$ s'anomena revestiment universal a l'espai revestiment simplement connex més petit possible. Es pot provar que un espai revestiment és únic llevat d'un cas d'homeomorfismes. En altres paraules un espai revestiment es diu universal si és simplement connex, i el seu primer grup d'homotopia és trivial.

Vegeu també

• fibrat
• Revestiment ramificat

Referències

• W.S. Massey. Introducció a la topologia algebraica . Reverté, S.A. 1982. ISBN 84-291-5091-9.

• C. Kosniowsky. A first course in algebraic topology . Cambridge Univ Press. 1980. ISBN 0-521-23195-7.