Recta

Una recta, o línia recta, és un objecte geomètric format per un conjunt d'infinits punts, infinitament llarg i infinitament prim, que no té curvatura.^[1][2][3] També es diu que els punts d'una recta estan alineats.

Les línies vermella i blava d'aquest gràfic tenen el mateix pendent; les línies vermella i verda tenen la mateixa intersecció amb l'eix y (creuen l'eix y en el mateix lloc).

Representació d'un segment de recta.

Definicions i postulats d'Euclides

Euclides, en el seu tractat anomenat Els Elements,^[4] estableix diverses definicions relacionades amb la línia i la línia recta:

• Una línia és una longitud sense amplada (Llibre I, definició 2).
• Els extrems d'una línia són punts (Llibre I, definició 3).
• Una línia recta és aquella que jeu per igual respecte dels punts que hi són (Llibre I, definició 4).

Característiques de la recta

• La recta es prolonga indefinidament en ambdós sentits.
• En geometria euclidiana, la distància més curta entre dos punts és la línia recta.
• La recta es pot definir com el conjunt de punts situats al llarg de la intersecció de dos plans.

Semirecta

Feix de raigs.

S'anomena semirecta^{[nota 1]} cadascuna de les dues parts en què queda dividida una recta en ser tallada a qualsevol dels seus punts. És la part d'una recta conformada per tots els punts que s'ubiquen cap a un costat d'un punt fix de la recta, anomenat origen, a partir del qual s'estén indefinidament en un sol sentit.

Semirecta oposada

La semirecta oposada d'una semirecta és l'altra sortida semirecta de la recta que defineix la primera.^[8][9]

• Cada semirecta només té una semirecta oposada.
• Una semirecta i la seva semirecta oposada tenen el mateix origen.

Posicions relatives de les rectes

• Dues rectes són coplanàries si poden estar contingudes en un mateix pla. En cas contrari es diu que les rectes es creuen.
• Dues rectes són paral·leles si són coplanàries i no tenen cap punt en comú.
• Dues rectes són secants si tenen un sol punt en comú. En aquest cas, també són coplanàries.
• Dues rectes són perpendiculars si es tallen formant angles de 90°.^[13]

Les rectes en geometria

En geometria, la recta és un conjunt d'infinits punts, subconjunt parcial dels infinits punts que formen un pla i que compleix unes determinades propietats. És un ens fonamental (juntament amb el punt i el pla) que no admet una definició més concreta. Simplement, s'enuncien les propietats i se n'accepta l'existència de forma axiomàtica. Aquestes propietats (no demostrables) són les següents:

1. Per dos punts diferents hi passa una recta i només una.

2. Si dos punts d'una recta estan en un pla, llavors tots els altres punts de la recta també estan continguts en aquest pla.

3. La recta és un conjunt de punts linealment ordenat, obert i dens, on:

• Linealment ordenat significa que, donada una terna de punts, A, B i C, si A precedeix B i B precedeix a C, llavors A precedeix a C.
• Obert significa que no existeix ni un primer ni un últim punt.
• Dens significa que entre dos punts d'una recta sempre n'hi ha infinits més, de manera que no existeixen punts consecutius.

4. Tota recta continguda en un pla estableix una divisió dels punts del pla no continguts en la recta en dues úniques regions tals que tot punt del pla exterior a la recta pertany a una o altra regió, i de manera que, escollits dos punts que pertanyin a diferents regions, la recta que els conté té un punt situat entre ells que pertany a la recta original i viceversa.

5. Per un punt exterior a una recta, hi passa una (i només una) recta tal que les dues estan contingudes en un mateix pla i no tenen entre elles cap punt en comú (paral·lela).

6. Donada una classificació dels punts d'una recta en dues regions que compleix:

• Existeixen punts de la recta d'una i altra regió.
• Tot punt de la recta pertany a una o altra regió.
• Tot punt d'una regió precedeix a tot punt de l'altra regió.

llavors existeix un sol punt de la recta tal que tots els punts que el precedeixen pertanyen a la primera regió i tots els punts que el segueixen pertanyen a la segona regió.

Temes relacionats amb els punts 4 i 6: semiplà, semirecta.

Altres propietats de les rectes

• Una recta i un punt no contingut en ella determinen un pla que passa per ells.

Demostració: per definició de recta, aquesta està formada per infinits punts, dels quals se'n consideren dos. Així, es té un conjunt de 3 punts no alineats. Una de les propietats axiomàtiques del pla és que per tres punts no alineats hi passa un pla i només un. Aquest pla que passa pels tres punts passa pel punt no contingut en la recta i també per la recta, ja que una de les propietats axiomàtiques de la recta (la segona) diu que si dos punts d'una recta estan en un pla, llavors tots els altres punts de la recta també estan continguts en aquest pla, QED.

• Dues rectes que es tallen determinen un pla que passa per elles (i per tant, són coplanàries).

Demostració: per definició de recta, aquesta està formada per infinits punts, dels quals se'n considera un d'una de les rectes que interseca. Aplicant la propietat anterior, se segueix que existeix un pla que passa per aquest punt i que conté tota l'altra recta, en particular el punt comú entre les dues rectes. Aquest pla, també conté la primera recta, ja que una de les propietats axiomàtiques de la recta (la segona) diu que si dos punts d'una recta estan en un pla, llavors tots els altres punts de la recta també estan continguts en aquest pla, QED.

• Si una recta (a) talla a una altra recta b, llavors a també talla totes les paral·leles a b contingudes en el pla que determinen a i b.

Demostració, per reducció a l'absurd: se suposa a que no talla a una paral·lela de b (c), continguda en el mateix pla que defineixen a i b, que intersequen al punt I. Llavors, pel punt I, exterior a c existirien dues rectes paral·leles a c, cosa que entra en contradicció amb una propietat axiomàtica de la recta (la cinquena).

• Si dues rectes (a i b) són paral·leles a una tercera (c), llavors són paral·leles entre si (propietat transitiva).

Demostració (encara no disponible a Viquipèdia).

Les rectes en matemàtiques

En un espai vectorial (per exemple R² o R³) es defineix la recta r com:

${\displaystyle r=\{{\vec {a}}+t{\vec {b}}\mid t\in \mathbb {R} \}}$

on ${\displaystyle {\vec {a}}}$ i ${\displaystyle {\vec {b}}}$ són vectors (per exemple de R² o R³) fixos i ${\displaystyle {\vec {b}}}$ és no nul. t és un paràmetre real lliure que és el paràmetre arc quan ${\displaystyle {\vec {b}}}$ és unitari. El vector b descriu la direcció de la recta i ${\displaystyle {\vec {a}}}$ és un punt de la recta. Aquesta equació és l'anomenada equació vectorial d'una recta.

De forma més abstracte, hom sovint assumeix que els punts d'una recta es corresponen d'un a un amb els nombres reals.

La recta en R²

Equacions de la recta en R²

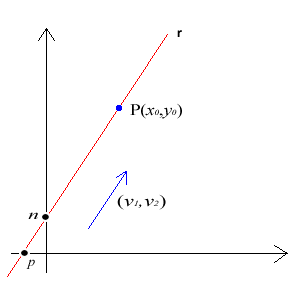
• Equació vectorial: ${\displaystyle r:(x,y)=(x_{0},y_{0})+{\lambda }\cdot (v_{1},v_{2})}$ on:
  • ${\displaystyle P(x_{0},y_{0})}$ és un punt per on passa la recta.
  • ${\displaystyle {\lambda }}$ és un paràmetre tal que ${\displaystyle {\lambda }\in \mathbb {R} }$
  • ${\displaystyle {\vec {v}}=(v_{1},v_{2})}$ és un vector que dona la direcció de la recta i s'anomena vector director de la recta.
• Equacions paramètriques: ${\displaystyle r:\left\{{\begin{matrix}x=x_{0}+{\lambda }\cdot v_{1}\\y=y_{0}+{\lambda }\cdot v_{2}\end{matrix}}\right.}$.

S'obtenen directament de desglossar l'equació vectorial.^[1]

• Equació contínua: ${\displaystyle r:{\frac {x-x_{0}}{v_{1}}}={\frac {y-y_{0}}{v_{2}}}}$

S'obté de plantejar la igualació del paràmetre λ de les dues equacions paramètriques. Les rectes paral·leles a algun dels eixos coordenats, no es poden expressar amb aquesta forma, ja que tindrien algun denominador nul.

• Equació general o implícita: ${\displaystyle r:A\cdot x+B\cdot y+C=0}$

amb A, B i C, coeficients reals fixos tals que A i B són no nuls.^[14]

Aquesta equació s'obté de l'equació contínua considerant:

${\displaystyle A=v_{2}}$

${\displaystyle B=-v_{1}}$

${\displaystyle C=v_{1}\cdot y_{0}-v_{2}\cdot x_{0}}$.

• Equació explícita ${\displaystyle r:y=m\cdot x+n}$

S'obté aïllant y en l'equació anterior i considerant:

${\displaystyle m=-{\frac {A}{B}}}$

${\displaystyle n=-{\frac {C}{B}}}$, on

• m s'anomena pendent de la recta i el seu valor és el de la tangent de l'angle (α) que forma la recta amb l'eix x.
• n és l'ordenada del punt d'intersecció entre la recta i l'eix y.^[2]

• Equació canònica ${\displaystyle r:{\frac {x}{p}}+{\frac {y}{n}}=1}$

Obtinguda dividint l'equació implícita per C i anomenant

${\displaystyle p=-{\frac {C}{A}}}$

${\displaystyle n=-{\frac {C}{B}}}$.

Els paràmetres resulten ser tals que la recta interseca amb els eixos de coordenades en els punts ${\displaystyle (p,0)}$ i ${\displaystyle (0,n)}$.

• Equació punt-pendent ${\displaystyle r:y-y_{0}=m\cdot (x-x_{0})}$

S'obté aïllant ${\displaystyle y-y_{0}}$ de l'equació contínua i considerant:

${\displaystyle m={\frac {v_{2}}{v_{1}}}}$, que torna a ser el pendent de la recta ja que ${\displaystyle A=v_{2}}$, ${\displaystyle B=-v_{1}}$ i s'havia definit m com ${\displaystyle m=-{\frac {A}{B}}}$

Aquesta equació és especialment útil, ja que permet escriure directament l'equació d'una recta, coneguts el pendent i un punt pertanyent a la recta.

Rectes notables R²

• L'equació d'una recta vertical, com la v, respon a l'equació

${\displaystyle x=x_{v}}$ (constant).

• L'equació d'una recta horitzontal, com la h, respon a l'equació

${\displaystyle y=y_{h}}$ (constant).

• Una recta qualsevol que passi per l'origen O (0,0), com la s, complirà la condició ${\displaystyle n=0}$, i la seva equació explícita serà de la forma ${\displaystyle r:y=m\cdot x}$.

Paral·lelisme i perpendicularitat

Dues rectes qualssevol (una representada amb primes (') sobre els seus paràmetres i l'altre no)

• Seran paral·leles si i només si (els següents tres punts són equivalents):
  • els seus vectors directors són paral·lels, cosa que passa quan ${\displaystyle {\frac {v_{1}}{v'_{1}}}={\frac {v_{2}}{v'_{2}}}}$
  • ${\displaystyle {\frac {A}{A'}}={\frac {B}{B'}}}$
  • ${\displaystyle m=m'}$
• Seran perpendiculars (o ortogonals) si i només si (els següents punts també són equivalents)
  • els seus vectors directors són ortogonals, cosa que passa quan el seu producte escalar és nul: ${\displaystyle v_{1}\cdot v'_{1}+v_{2}\cdot v'_{2}=0}$
  • ${\displaystyle A\cdot A'+B\cdot B'=0}$
  • ${\displaystyle m\cdot m'=-1}$

Angles i distàncies

Angle entre dues rectes: Dues rectes que es tallen defineixen quatre angles iguals dos a dos. L'angle (α) que formen les rectes es defineix tal que està entre 0 i 90°. Coneguts els vectors directors amb l'expressió que defineix el que formen els seus vectors directors ${\displaystyle {\vec {v}}}$ i ${\displaystyle {\vec {w}}}$, es pot calcular l'angle que formen amb l'expressió:

${\displaystyle \cos \alpha ={\frac {|{\vec {v}}\cdot {\vec {w}}|}{|{\vec {v}}||{\vec {w}}|}}}$

Distància entre un punt i una recta: La distància entre una recta (${\displaystyle r:A\cdot x+B\cdot y+C=0}$ ) i un punt ${\displaystyle P(p_{1},p_{2})}$ exterior a r és la menor de les distàncies entre el punt P i qualsevol dels punts de la recta r. Aquesta distància es minimitza amb la projecció ortogonal de P sobre r, i l'expressió que dona la distància entre P i r' és:

${\displaystyle d(P,r)={\frac {|A\cdot p_{1}+B\cdot p_{2}+C|}{\sqrt {A^{2}+B^{2}}}}}$

Distància entre dues rectes: la distància entre dues rectes és la menor distància entre punts d'una i altra recta. Si les rectes tenen algun punt en comú (si són secants), la distància és 0; si són paral·leles, la distància entre elles ve donada per la distància entre un punt d'una recta i l'altra recta, ja que aquest valor és independent del punt triat.

Si ${\displaystyle r:A\cdot x+B\cdot y+C=0}$ i ${\displaystyle r':A'\cdot x+B'\cdot y+C'=0}$ són dues rectes paral·leles del pla i ${\displaystyle P(p_{1},p_{2})}$ un punt pertanyent a r, llavors la distància entre r i r' és:

${\displaystyle d(r,r')=d(P,r')={\frac {\left|A'\cdot p_{1}+B'\cdot p_{2}+C'\right|}{\sqrt {(A')^{2}+({B}')^{2}}}}}$

Equació de la recta a l'espai

Recta determinada mitjançant un sistema d'equacions

Sistema de 2 equacions i 3 variables.

Recta a l'espai usant un sistema de 2 equacions i 3 incògnites:

${\displaystyle \left\{{\begin{matrix}x&+y&+z&=4\\x&-y&+3z&=7\end{matrix}}\right.}$

• Aquesta equació equival a la intersecció de dos plans a l'espai.

Recta determinada mitjançant vectors

Recta a l'espai usant un punt, ${\displaystyle p=(p_{x},p_{y},p_{z})}$, i un vector, ${\displaystyle u=(u_{x},u_{y},u_{z})}$:

${\displaystyle (x,y,z)=(p_{x},p_{y},p_{z})+\lambda (u_{x},u_{y},u_{z})}$

• Al vector ${\displaystyle u\,}$ se'n diu vector director.

Posicions relatives entre rectes

• Dues rectes seran paral·leles si tenen vectors directors paral·lels.
• Dues rectes seran coincidents si comparteixen almenys dos punts diferents.
• Dues rectes s'intersequen si no són paral·leles i tenen un punt en comú.
• Dues rectes seran coplanàries^[8] si estan contingudes en algun pla.
  • Dues rectes són coplanàries si i només si o bé són coincidents o bé s'intersequen o bé són paral·leles.
• Dues rectes es creuen si no són paral·leles ni tenen punts comuns.

Notes

1. També s'usa raig el qual és un possible anglicisme de ray^[5] a Hispanoamèrica. En alguns textos és esmentat com a raig o semirecta^[6] però predomina l'ús de semirecta en bibliografia abundant^{[7][8][9][10][11][12]} que no recullen cap altra alternativa.

Referències

1. Line a MathWorld (anglès)
2. «line | mathematics | Britannica» (en anglès). [Consulta: 21 gener 2022].
3. «▷ ¿Qué es una línea recta? - Definición y ejemplos» (en castellà), 23-09-2020. [Consulta: 21 gener 2022].
4. www.euclides.org: Los Elementos Arxivat 2009-03-06 a Wayback Machine.
5. Weisstein, Eric W., «Ray» a MathWorld (en anglès).
6. Pequeña enciclopedia de matemáticas. Pagoulatos, 1981.
7. «semirrecta». Diccionario de la lengua española. Real Academia Española (castellà).
8. Real Academia de Ciencias Exactas, Física y Naturales. Diccionario esencial de las ciencias. Espsa, 1999. ISBN 84-239-7921-0.
9. Diccionario de matematicas. Akal Editores, 1979.
10. Docta guia educativa. Carroggio,s.a..
11. Enciclopedia didáctica de matemáticas. Oceano.
12. Léxico de matemáticas. Akal Editores.
13. «rectas» (en castellà). [Consulta: 21 gener 2022].
14. «Equations of a Straight Line». [Consulta: 29 gener 2022].

Vegeu també

• Axiomes de la geometria
• Recta numèrica
• Segment lineal

Viccionari