Elementární funkce

Jako elementární funkce je označována funkce, kterou lze získat konečným počtem sečtení, odečtení, násobení, dělení a složení základních elementárních funkcí, jedná se tedy o algebraické funkce a nižší transcendentní funkce, jako logaritmické, exponenciální, mocninné, goniometrické, cyklometrické, hyperbolické a hyperbolometrické funkce. Funkce, které nelze vyjádřit prostřednictvím konečného počtu elementárních funkcí, se označují jako vyšší transcendentní funkce.

Základní elementární funkce

Definice logaritmu a exponenciály

Exponenciální a logaritmická funkce při základu ${\displaystyle 2}$

Funkci přirozeného logaritmu ${\displaystyle \ln$ :\mathbb {R} \rightarrow \mathbb {R} } lze zavést axiomaticky:

• definiční obor funkce je otevřený interval ${\displaystyle (0,+\infty )}$
• pro každé dva prvky ${\displaystyle x}$ a ${\displaystyle y}$ definičního oboru platí: ${\displaystyle \ln(xy)=\ln(x)+\ln(y)}$
• pro každé dva prvky ${\displaystyle x>y}$ definičního oboru platí: ${\displaystyle \ln(x)>\ln(y)}$
• pro prvky ${\displaystyle x}$ definičního oboru platí: ${\displaystyle \lim _{x\rightarrow 1}{\frac {\ln(x)}{x-1}}=1}$

Výše uvedené čtyři axiomy splňuje právě jedna funkce, tj. funkce přirozený logaritmus. Exponenciální funkci ${\displaystyle e^{x}}$ pak můžeme definovat jako inverzi přirozeného logaritmu ${\displaystyle \ln x}$ a její pomocí definovat obecnou mocninnou funkci:

${\displaystyle g(x)^{f(x)}=e^{f(x)\ln g(x)}}$ kde funkce ${\displaystyle g}$ je na svém definičním oboru kladná. Je-li funkce ${\displaystyle f}$ resp. ${\displaystyle g}$ konstantní resp. identická funkce, dostáváme mocninnou funkci s reálným exponentem ${\displaystyle x^{a}}$, je-li funkce ${\displaystyle f}$ resp. ${\displaystyle g}$ identická resp. konstantní funkce, dostáváme exponenciální funkci při reálném základu ${\displaystyle a^{x}}$. Pomocí funkce ${\displaystyle e^{x}}$ lze zavést funkce hyperbolické a jejich inverzí funkce hyperbolometrické.

Definice sinu

Sinus a kosinus jako jeho posunutí

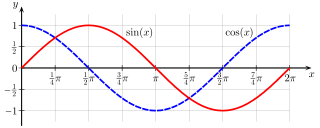
Funkci sinu ${\displaystyle \sin$ :\mathbb {R} \rightarrow \mathbb {R} } lze zavést axiomaticky:

• definiční obor funkce je reálná osa ${\displaystyle \mathbb {R} }$
• ${\displaystyle \sin(0)=0}$
• pro každé dva prvky ${\displaystyle x}$ a ${\displaystyle y}$ definičního oboru platí: ${\displaystyle \sin(x+y)+\sin(x-y)=2\sin(x)\sin({\frac {\pi }{2}}-y)}$
• pro každé dva prvky ${\displaystyle x>y}$ z uzavřeného intervalu ${\displaystyle \langle 0,{\frac {\pi }{2}}\rangle }$ platí: ${\displaystyle \sin(x)>\sin(y)}$
• pro prvky ${\displaystyle x}$ definičního oboru platí: ${\displaystyle \lim _{x\rightarrow 0}{\frac {\sin(x)}{x}}=1}$

Výše uvedených pět axiomů splňuje právě jedna funkce, tj. funkce sinus, jejíž pomocí lze zavést funkce goniometrické a jejich inverzí funkce cyklometrické.

Vlastnosti

Elementární funkce jsou na svém definičním oboru kromě případných izolovaných bodů:

• spojité,
• diferencovatelné,
• integrovatelné, tj. existují k nim primitivní funkce.

Příklady

Příklady elementárních funkcí:

• ${\displaystyle \ln(-x^{2})}$,
• ${\displaystyle {\sqrt {\sin ^{2}(x)}}=\left|\sin(x)\right|}$,
• ${\displaystyle {\frac {e^{\tan(x)}}{1+x^{2}}}\sin \left({\sqrt {1+\ln ^{2}x}}\,\right)}$.

Příkladem funkce, která není elementární, je chybová funkce: ${\displaystyle \mathrm {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt}$.

Literatura

• BARTSCH, Hans-Jochen. Matematické vzorce. 4. vyd. Praha: Academia, 1994. 832 s. ISBN 80-200-1448-9.

Související články

• Funkce

Externí odkazy

• Obrázky, zvuky či videa k tématu elementární funkce na Wikimedia Commons
• Elementární funkce - studijní materiál VŠB

Portály: Matematika