Hohmannova elipsa

Hohmannova elipsa, též Hohmannova trajektorie či Hohmannova přechodová dráha (podle ČSN 310001 je toto označení nesprávné), je z hlediska spotřeby paliva za jistých podmínek optimální cesta pro přelet mezi dvěma kruhovými drahami okolo centrálního tělesa.

Hohmannova elipsa (žlutě)

V sovětské a ruské literatuře je někdy označována jako Hohmann-Vetčinkinova dráha, protože stejný koncept na svých veřejných přednáškách v letech 1921-1925 zmiňoval ruský matematik Vladimir Petrovič Vetčinkin. Nazývá se podle německého vědce Waltera Hohmanna, který o ní publikoval v roce 1925 a byl první, kdo diskutoval její optimalitu. Náčrty této dráhy použil už v roce 1911 Konstantin Eduardovič Ciolkovskij.

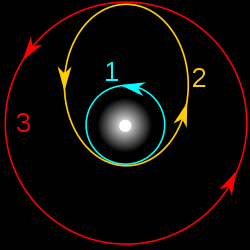
Přechod mezi kruhovými orbitami je zajištěn dvěma krátkými zážehy. První zážeh vyšle satelit na eliptickou dráhu tím, že pozvedne nejvyšší bod dráhy (apoapsidu). Druhý zážeh, který je proveden když satelit doletí do apoapsidy, zvedne nejnižší část orbity (periapsidu). Dráha mezi zážehy má tvar půlelipsy, která se ve vrcholech dotýká obou kruhových orbit. Právě tento eliptický úsek dráhy satelitu se nazývá Hohmannova elipsa.^[1]

Pro přelet mezi dvěma kruhovými drahami v Newtonovském gravitačním poli se jedná za jistých podmínek o optimální přechodovou dráhu. Pokud je poměr mezi poloměry počáteční a cílové orbity větší, než 11,74, je energeticky výhodnější použít bieliptickou přechodovou dráhu. Je používána pro umisťování družic na geostacionární dráhu a pro lety k Marsu a Venuši. Ke vzdálenějším planetám je z důvodu úspory paliva volena obvykle mnohem složitější dráha s řadou gravitačních manévrů.

Vlastnosti

Eliptická dráha s minimální energií spojující dva zadané body má tu vlastnost, že (alespoň) jedno z ohnisek leží na spojnici těchto bodů. Další vlastností energeticky optimálních drah je, že radiální rychlosti (vzhledem k centru gravitace) jsou v zadaných bodech až na znaménko stejné a jejich součet je nulový. ^[2]

Hohmannova orbita představuje speciální případ, kdy jsou body na opačných stranách od centrálního tělesa. Na spojnici tak leží obě ohniska a zadané body splývají s apsidami eliptické orbity. Díky tomu jsou radiální rychlosti v obou bodech jsou nulové.

Matematický popis

Z vis–viva rovnice pro rychlost ${\displaystyle v}$, vzdálenost od centra ${\displaystyle r}$ a velkou poloosu ${\displaystyle a}$ vyplývá

${\displaystyle v={\sqrt {\mu \left({\frac {2}{r}}-{\frac {1}{a}}\right)}}}$,

kde ${\displaystyle \mu =G(M+m)\approx GM}$ (${\displaystyle M}$ a ${\displaystyle m}$ jsou hmotnosti centrálního tělesa a družice, ${\displaystyle G}$ je gravitační konstanta). Pomocí této rovnice lze vypočíst rychlosti družice v libovolném místě na obecné orbitě. Na kruhových orbitách o poloměrech ${\displaystyle r_{1},r_{2}}$ má družice rychlosti ${\displaystyle v_{1},v_{2}}$ a na Hohmannově elipse v nejnižším a nejvyšším bodě rychlosti ${\displaystyle v_{h1},v_{h2}}$. Pro Hohmannovu elipsu platí ${\displaystyle a={\frac {r_{1}+r_{2}}{2}}}$ a pro kruhové dráhy ${\displaystyle a=r_{1},r_{2}}$.

${\displaystyle v_{1}={\sqrt {\mu \left({\frac {2}{r_{1}}}-{\frac {1}{r_{1}}}\right)}}={\sqrt {\frac {\mu }{r_{1}}}}}$

${\displaystyle v_{h1}={\sqrt {\mu \left({\frac {2}{r_{1}}}-{\frac {2}{r_{1}+r_{2}}}\right)}}>v_{1}}$,

${\displaystyle v_{h2}={\sqrt {\mu \left({\frac {2}{r_{2}}}-{\frac {2}{r_{1}+r_{2}}}\right)}}<v_{2}}$,

${\displaystyle v_{2}={\sqrt {\mu \left({\frac {2}{r_{2}}}-{\frac {1}{r_{2}}}\right)}}={\sqrt {\frac {\mu }{r_{2}}}}}$,

Celková změna rychlosti ${\displaystyle \Delta v}$, která je třeba pro manévr se dá rozdělit na dva členy: vstoupení na Hohmannovu elipsu (${\displaystyle \Delta v_{1}}$) a pak na cílovou kruhovou dráhu (${\displaystyle \Delta v_{2}}$). Změny rychlostí se dají vyjádřit pomocí rozdílu rychlostí na jednotlivých úsecích dráhy.

${\displaystyle \Delta v=\Delta v_{1}+\Delta v_{2}=\vert v_{h1}-v_{1}\vert +\vert v_{2}-v_{h2}\vert }$.

Energetická náročnost

Potřebná změna rychlosti sondy pro přelet mezi kruhovými dráhami v závislosti na poměru velikostí drah.

Potřebná změna rychlosti závisí na vzájemné velikosti kruhových orbit.

${\displaystyle \Delta v_{1}=v_{h1}-v_{1}=v_{1}\left({\sqrt {\frac {2r_{2}}{r_{1}+r_{2}}}}-1\right)}$

${\displaystyle \Delta v_{2}=v_{h2}-v_{2}=v_{2}\left(1-{\sqrt {\frac {2r_{1}}{r_{1}+r_{2}}}}\right)}$

Rychlosti lze převést do bezrozměrné formy tím, že se změny rychlostí uvedou jako poměr k rychlosti na příslušné kruhové orbitě (předchozí dvě rovnice se vydělí postupně ${\displaystyle v_{1},v_{2}}$). Celková změna rychlosti se uvede v poměru k ${\displaystyle v_{1}}$.

${\displaystyle {\frac {\Delta v}{v_{1}}}={\frac {\Delta v_{1}}{v_{1}}}+{\frac {\Delta v_{2}}{v_{1}}}={\frac {\Delta v_{1}}{v_{1}}}+{\sqrt {\frac {r_{1}}{r_{2}}}}{\frac {\Delta v_{2}}{v_{2}}}={\frac {\Delta v_{1}}{v_{1}}}+{\frac {1}{\sqrt {R}}}{\frac {\Delta v_{2}}{v_{2}}}}$

Zde byla zavedena bezrozměrná proměnná ${\displaystyle R={\frac {r_{2}}{r_{1}}}}$. Bezrozměrná velikost ${\displaystyle R}$ umožní přepsat rovnici pomocí jediné proměnné.

${\displaystyle {\frac {\Delta v}{v_{1}}}={\sqrt {\frac {2R}{R+1}}}-1+{\frac {1}{\sqrt {R}}}\left(1-{\sqrt {\frac {2}{R+1}}}\right)}$

Pro nalezení minima či maxima stačí výraz zderivovat a derivaci položit rovnou nule.

${\displaystyle {\frac {d}{dR}}\left({\frac {\Delta v}{v_{1}}}\right)={\frac {1}{(R+1)^{2}}}\left({\frac {2R}{R+1}}\right)^{-1/2}-{\frac {1}{\sqrt {R}}}{\frac {1}{(R+1)^{2}}}\left({\frac {2}{R+1}}\right)^{-1/2}+{\frac {1}{R^{3/2}}}{\sqrt {\frac {2}{R+1}}}-{\frac {1}{2R^{3/2}}}}$

${\displaystyle {\frac {d}{dR}}\left({\frac {\Delta v}{v_{1}}}\right)=0\Leftrightarrow R^{3}-15R^{2}-9R-1=0}$^{[pozn. 1]}

Kubická rovnice na pravé straně má pouze jedno kladné řešení, které je přibližně ${\displaystyle R\approx 15,5817}$. Jedná se o poměr velikostí počáteční a cílové orbity, pro které se spotřebuje při Hohmannově přechodu maximum energie. :${\displaystyle \left({\frac {\Delta v}{v_{1}}}\right)_{max}\approx 0,536}$

Pro poměr ${\displaystyle R>15,5\dots }$ je energetická náročnost s rostoucí velikostí cílové orbity menší. Jedná se o zdánlivě paradoxní závěr, že přechod na vyšší orbitu může vyžadovat méně energie. Na Hohmannově elipse se ale část energie spotřebuje na srovnání eliptické dráhy na kruhovou. Tento proces je účinnější pro vzdálené cílové orbity, na kterých se družice pohybuje pomalu. Druhý zážeh tak spotřebuje mnohem menší množství energie. ^{[pozn. 2]}

V limitním případě, kdy ${\displaystyle R\to \infty }$ se Hohmannova elipsa stane parabolou, druhý zážeh není nutný (${\displaystyle \Delta v_{2}=0}$) a rychlost, na kterou musíme těleso urychlit při prvním zážehu je identická s únikovou rychlostí (konkrétně pro Zemi se jedná o 2. kosmickou rychlost).

Příklad

Přelet Země-Mars: oběžná dráha Země (tyrkysová), 2 Hohmannova elipsa (žlutá) und oběžná dráha Marsu (červená)

Přechodová orbita použitá misí Mars Reconnaissance Orbiter.

Mars se nachází nejblíže zemi, když je v opozici. Sondy mohou této blízkosti využít pouze pokud vynaloží velké množství energie, protože by potřebovaly zrychlovat proti směru oběhu Země kolem Slunce.

Energeticky nejméně náročná dráha je Hohmannova elipsa.^{[pozn. 3]} Zde naopak sonda dosáhne Marsu v konjunci (na opačné straně, než kde vystartovala při pohledu ze slunce). Velká poloosa elipsy je rovna aritmetickému průměru vzdáleností Země-Slunce a Slunce-Mars (v místech, kde se potkávají s elipsou). Podle Keplerova třetího zákona tak pro půlelipsu vychází doba letu přibližně osm a půl měsíce.

Na začátku se sonda nachází na oběžné dráze Země. Prvním zážehem motorů se urychlí, opustí Zemi a dostane se na eliptickou dráhu k Marsu. Když doletí do blízkosti Marsu, dalším spuštěním motorů se dostane na jeho orbitu. Hohmannova elipsa je k drahám planet tečná a není tak třeba vyrovnávat radiální pohyb sondy. Radiální rychlost vzhledem ke Slunci je v obou místech spuštšní motorů nulová.

Další ušetření paliva sondy nabízí metoda, při níž se sonda přiblíží libračním centrům cílového tělesa, kolem nichž vhodným způsobem obíhá a ztrácí tak energii, což šetří palivo nutné k druhému zážehu. Tento postup poprvé použila roku 1986 sonda SMART-1, když se přibližovala k Měsíci.

Na obrázku vpravo je vykreslena dráha sondy Mars Reconnaissance Orbiter, která využila jinou dráhu, než energeticky optimální Hohmannovu elipsu, ale její cesta k Marsu trvala pouze 7 měsíců.