System cyfesurynnau polar

Mewn mathemateg, mae'r system cyfesurynnau polar yn system o gyfesurynnau o fewn y gofod dau ddimensiwn lle mae pob pwynt ar y plân yn cael ei bennu gan bellter o bwynt cyfeiriol ac ongl. Defnyddir yr un termau ag a ddefnyddir o fewn y system gyfesurynnol Cartesaidd:

• y tarddiad, sef y pwynt cyfeiriol a'r
• echelin begynol (polar axis)

Pwyntiau o fewn y system cyfesurynnau polar, gyda tarddiad O ac echelin begynol L. Mewn gwyrdd, mae'r pwynt gyda chyfesuryn rheiddiol 3 a chyfesuryn onglaidd o 60 gradd neu (3, 60°). Mewn glas, ceir y pwynt (4, 210°).

Gelwir y pellter o'r tarddiad yn "gyfesuryn rheiddiol", neu "radiws", a'r ongl yn "gyfesuryn onglaidd", "ongl begynol" neu'n "asimwth".^[1][2]

Hanes

Creeodd y seryddwr Hipparchus (190–120 CC) dabl o ffwythiannau'r cord (table of chord functions) gan roi hyd cord pob ongl, a cheir tystiolaeth iddo ddefnyddio cyfesurynnau pegynol wrth nodi lleoliad y sêr.^[3] Yn ei lyfr Ar Sbiralau, disgrifiodd Archimedes yr hyn a elwir heddiw yn sbiral Archimedes, ffwythiant ble mae'r radiws yn dibynnu ar yr ongl; fodd bynnag ni ddisgrifiodd y system cyfesurynnau polar llawn, na'i ddiffinio. Yn y 17g cyflwynwyd y cysyniad o system cyfesurynnau polar gan ddau fathemategydd, yn annibynnol o'i gilydd: Grégoire de Saint-Vincent a Bonaventura Cavalieri.

Confensiynau

Grid polar (neu 'begynol') gyda sawl ongl, sy'n cynyddu fel cyfeiriad ccw, wedi'u labelu mewn graddau.

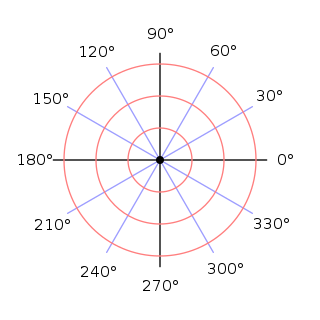
Dynodir y cyfesuryn rheiddiol yn aml gan r neu ρ, a'r cyfesuryn onglaidd gan φ, θ, neu t. Mae ISO 31-11 yn dynodi'r cyfesuryn onglaidd fel φ ond o fewn llenyddiaeth mathemategol, bron yn ddieithriad, defnyddir &theta yn hytrach na φ.

Y mynegiant arferol ar gyfer onglau yw naill ai 'gradd' neu 'radian' (2π rad = 360°). Defnyddir graddau o fewn fforio a mapio, defnyddir radianau o fewn mathemateg a ffiseg.^[4]