Teilio Ewclidaidd

Mae teilio polygonau rheolaidd amgrwn yn y plân Ewclidaidd yn ffurf celf sy'n bodoli cyn hanes, ac yn faes o fewn geometreg Ewclidaidd. Cychwynwyd ei ystyried yn faes mathemateg gan Kepler yn ei Harmonices Mundi (Lladin am "Cynghanedd Bywyd") yn 1619.

Teilio Ewclidaidd

Math	Brithwaith

Enghraifft o deilio cyfnodol

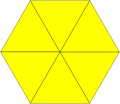
Teilio rheolaidd: un math o ochrau (arwynebau) rheolaidd	Teilio rhan-reolaidd neu 'deilio unffurf': un math o fertig, ond dau neu ragor o arwynebau gwahanol
Mae gan deilio k-unffurf sawl fertig (nifer = k) a dau neu fwy o ochrau rheolaidd.	Mae teilio nad yw'n ochr-i-ochr yn caniatau maint ochrau gwahanol.

Mewn teilio Ewclidaidd ochr-wrth-ochr, ymyl-i-ymyl, mae'n rhaid i gyfanswm onglau mewnol y polygonau sy'n cwrdd ar fertig fod yn 360 gradd.

Teilio rheolaidd

Teilio rheolaidd (3)

p6m, *632		p4m, *442
36 (t=1, e=1)	63 (t=1, e=1)	44 (t=1, e=1)

Teilio rheolaidd

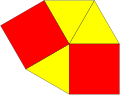
Teilio Archimedaidd, neu deilio unffurf, neu led-rheolaidd.^[1]

Teilio unffurf (8)

p6m, *632
3.122 (t=2, e=2)	3.4.6.4 (t=3, e=2)	4.6.12 (t=3, e=3)	(3.6)2 (t=2, e=1)
p4m, *442	p4g, 4*2	cmm, 2*22	p6, 632
4.82 (t=2, e=2)	32.4.3.4 (t=2, e=2)	33.42 (t=2, e=3)	34.6 (t=3, e=3)

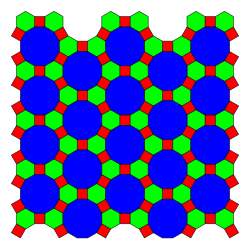
Teilio k-unffurf

teilio 3-unffurf #57 o 61 lliw

gan ochrau, trionglau melyn, sgwariau coch.

gan lleoliadau 4-isohedral, 3 lliw'r trionglau

Gellir dosbarthu teilio cyfnodol gan nifer orbidau'r fertigau (corneli), ymyl a theiliau. Os oes k orbid o fertigau, adnabyddir y teilio fel k-unffurf neu k-isogonal; os oes t orbid o deils, fe'u gelwir yn t-isohedral; ac os oes e orbid o ymylon, yna'n e-isotoxal.^[2][3][4][5]

Gellir adnabod teilio k-unffurf gyda'r un fertig drwy'r system cymesuredd y grŵp papur wal.^[6]

cyfrifiad teilio k-unffurf, m-Archimedaidd

		m									Total
		1	2	3	4	5	6	7	8	9
k	1	11	0	0	0	0	0	0	0	0	11
	2	0	20	0	0	0	0	0	0	0	20
	3	0	22	39	0	0	0	0	0	0	61
	4	0	33	85	33	0	0	0	0	0	151
	5	0	74	149	94	15	0	0	0	0	332
	6	0	100	284	187	92	10	0	0	0	673
	7	0	?	?	?	?	?	7	0	0	?
	8	0	?	?	?	?	?	20	0	0	?
	9	0	?	?	?	?	?	?	8	0	?
	10	0	?	?	?	?	?	?	27	0	?
	11	0	?	?	?	?	?	?	?	1	?

Eraill

Ar gyfer teilio Ewclidaidd ochr-wrth-ochr, ymyl-i-ymyl, mae'n rhaid i gyfanswm onglau mewnol y polygonau sy'n cwrdd ar fertig fod yn 360 gradd. Mae gan n-gon rheolaidd onglau mewnol ${\displaystyle \left(1-{\frac {2}{n}}\right)180}$ gradd. Ceir 17 o bolygonau rheolaidd gwahanol, sydd a'u honglau mewnol yn adio i 360 gradd. Gelwir bob un o'r rhain yn 'rywogaeth' o fertig.

Gweler hefyd

• Grŵp papur wal