Apollonius
From Wikipedia, the free encyclopedia
Remove ads
Apollonius af Perga (eller Perge ca. 262 f.Kr. – 190 f.Kr.) var en græsk geometer og astronom, anerkendt for sit arbejde om keglesnit. Det var Apollonius, som gav ellipse, parabel, og hyperbel de navne som vi kender i dag.
Hypoteserne om excentrisk kredsløb, eller ækvivalent, deferent og epicykel til at forklare den tilsyneladende bevægelse af planeterne og den varierende fart af månen, var også hans.
 For alternative betydninger, se Apollonius (flertydig). (Se også artikler, som begynder med Apollonius)
For alternative betydninger, se Apollonius (flertydig). (Se også artikler, som begynder med Apollonius)

Kun lidt er kendt om hans liv. Han studerede og arbejdede i Alexandria på den tid, faraoerne Ptolemaios III og Ptolemaios IV regerede. Der havde Euklid grundlagt en matematiske skole, som fik stor betydning. Af hans bøger fremgår det, at Apollonios besøgte Pergamon, hvor der også fandtes et stort bibliotek som i Alexandria.
Remove ads
Videnskabelige bidrag
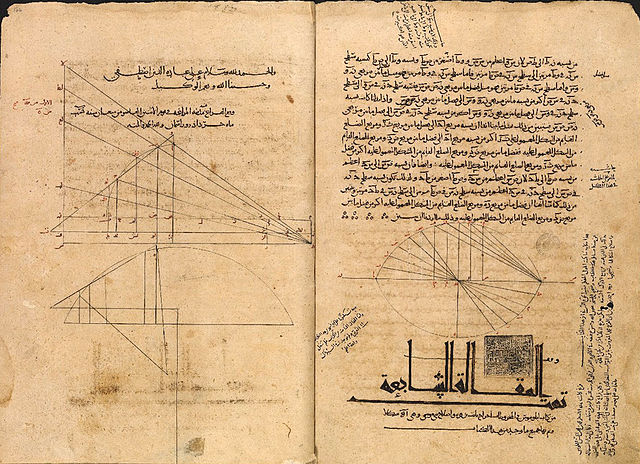
Apollonios' værk om keglesnit (κωνικά) var oprindelig i otte bøger. De første fire overlevede som på græsk, mens de fire andre ikke formodedes at eksistere længere. Men i 1600-tallet blev de tre næste bøger i arabisk oversættelse fundet i Biblioteca Medicea Laurenziana i Firenze og publiceret på latin i 1661. Den ottende bog er nu antaget at være gået tabt.
De tre første bøger ser ud til at give en opsummering om det, som på den tid allerede var kendt om keglesnit. I tredje bog blev for første gang klarlagt sammenhængene mellem pol og polare samt betydningen af harmonisk konjugerede punkter. Fra og med fjerde bog præsenteres egne bidrag. Han gav her en ny og bedre definition af disse kurver, som snittet mellem en vilkårlig kegle og et plan. Afhængig af orienteringen af planet i forhold til keglen, kan der opstå tre typer af keglesnit, som han gav navnene ellipse, hyperbel og parabel. I de følgende bøger kunne han så udlede nye egenskaber ved disse som blandt andet har med tangenter og normaler til sådanne geometriske kurver.
Andre geometriske problemer, som han studerede, var at finde det geometriske sted for de punkt hvis afstand til to givne punkter har et konstant forhold. Løsningen, som han fandt, kaldes ofte for Apollonios' cirkel. Tilsvarende problem med geometrisk sted for punkt med afstande til tre eller fire linjer i bestemte forhold løste han også ved at vise, at det var keglesnit. Det blev senere generaliseret af Pappos til at involvere mere end fire linjer og er derfor blevet kaldt Pappos' problem. Det spillede en vigtig rolle, da Descartes opdagede det koordinater, som lagde grundlaget for analytisk geometri.
Apollonios viste også, hvordan man kunne konstruere en cirkel, som berørte tre andre geometriske objekter, som kunne være et eller flere punkter, linjer eller cirkler. For det sidste tilfælde med alene cirkler fandt en meget elegant og smuk løsning, som senere fået navnet Apollonios' cirkler.
Han var også optaget af astronomi og især Månen og planeternes bevægelser. Han udviklede teorien om epicykler og viste, at det var ækvivalent med excentrisk bevægelse i en cirkel. Omtrent samtidig blev dette teoretiske grundlag benyttet af Hipparkhos i hans analyse af astronomiske observationer.
Remove ads
Litteratur
- M. Kline, Mathematical Thought from Ancient to Modern Times, Vol. I, Oxford University Press, Oxford (1972). ISBN 978-0-19-506135-2.
- C.B. Boyer, A History of Mathematics, Princeton University Press, New Jersey (1985). ISBN 0-691-02391-3.
Eksterne henvisninger
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads

