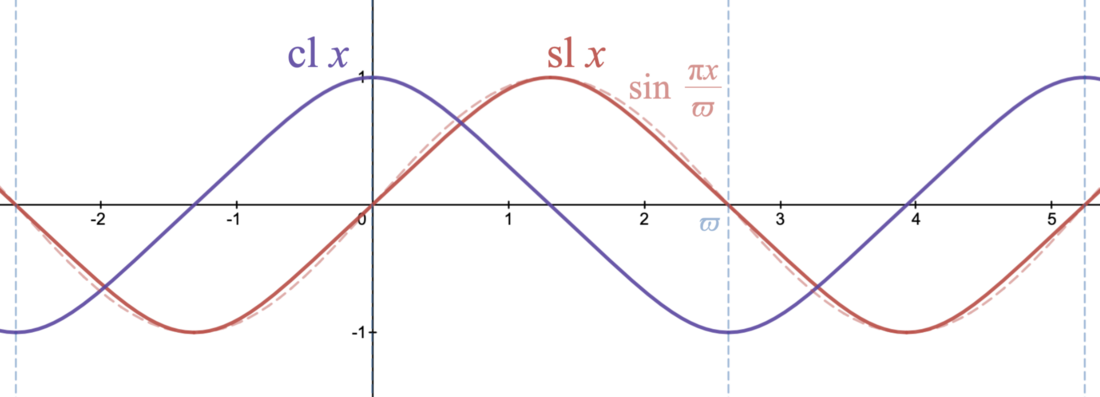
Sinus lemniscatus und Cosinus lemniscatus

Der lemniskatische Sinus (lateinisch Sinus lemniscatus) und der lemniskatische Kosinus (lateinisch Cosinus lemniscatus), abgekürzt mit ${\displaystyle \operatorname {sinlemn} }$ und ${\displaystyle \operatorname {coslemn} }$ oder ${\displaystyle \operatorname {sl} }$ und ${\displaystyle \operatorname {cl} }$, sind zwei spezielle, von Carl Friedrich Gauß eingeführte mathematische Funktionen. Sie haben für die Lemniskate von Bernoulli die entsprechende Bedeutung wie die Sinus- und die Kosinusfunktion für den Kreis.

Lemniskatischer Sinus (rot) und lemniskatischer Kosinus (blau) für ein reelles Argument, im Vergleich mit der trigonometrischen Sinusfunktion ${\displaystyle y=\sin(\pi x/\varpi )}$ (blassrosa gestrichelt).

Die Länge s des Lemniskatenbogens vom Ursprung korreliert mit dem Abstand r des Kurvenpunktes zum Ursprung.
Jeder Quadrant enthält einen Viertelbogen (der Länge ${\displaystyle {\tfrac {\varpi }{2}}}$) der Lemniskate. Die Brennpunkte liegen hier bei ${\displaystyle \left(\pm {\tfrac {1}{\sqrt {2}}}\mid 0\right)}$.

Die Funktionen ${\displaystyle \operatorname {sl} }$ und ${\displaystyle \operatorname {cl} }$ lassen sich zu meromorphen Funktionen in ${\displaystyle \mathbb {C} }$ (Menge der komplexen Zahlen) fortsetzen. Sie erfüllen die Periodizitätseigenschaften

${\displaystyle {\begin{aligned}\operatorname {sl} (z+2\varpi )=\operatorname {sl} (z),\qquad &\operatorname {sl} (z+2\mathrm {i} \varpi )=\operatorname {sl} (z),\\\operatorname {cl} (z+2\varpi )=\operatorname {cl} (z),\qquad &\operatorname {cl} (z+2\mathrm {i} \varpi )=\operatorname {cl} (z),\end{aligned}}}$

wobei ${\displaystyle \varpi =2{,}62205\ldots }$ die lemniskatische Konstante ist, und gehören daher (als historisch erste Beispiele) zu den elliptischen Funktionen.

Der lemniskatische Kosinus kann direkt vom lemniskatischen Sinus abgeleitet werden. Verschiebt man nämlich den Graphen der Funktion ${\displaystyle \operatorname {sl} }$ um ${\displaystyle {\tfrac {\varpi }{2}}}$ nach links, so entsteht der Graph von ${\displaystyle \operatorname {cl} }$.

Geschichte

Der 19-jährige Gauß beschäftigte sich 1796 (in erst nach seinem Tod veröffentlichten Notizen) mit der Frage, wie man aus einer gegebenen Bogenlänge ${\displaystyle s}$ einer Lemniskate den Abstand ${\displaystyle r\in (-1,1)}$ des entsprechenden Punktes auf der Kurve vom Koordinatenursprung ${\displaystyle r=0}$ berechnen kann. Mathematisch führt das auf die Umkehrfunktion ${\displaystyle r=r(s)}$ des elliptischen Integrals

${\displaystyle s(r)=\int _{0}^{r}{\frac {\mathrm {d} \,\rho }{\sqrt {1-\rho ^{4}}}}.}$

Beweis:

Für den ersten und dritten Quadranten kann die Lemniskate von Bernoulli auf folgende Weise parametrisiert werden: x und y als Koordinaten eines Punktes auf der Kurve im Abstand r vom Ursprung (Pythagoras) erfüllen die Lemniskatengleichung. Aus diesen zwei Gleichungen ergeben sich

${\displaystyle x(r)=r{\sqrt {1+r^{2}}}/{\sqrt {2}}}$ und ${\displaystyle y(r)=r{\sqrt {1-r^{2}}}/{\sqrt {2}}}$

Für die Berechnung der vom Ursprung ausgehenden Kurvenlänge s wird der Pythagoras der ersten Ableitungen von x und y gebildet und dieser integriert:

${\displaystyle s(r)=\int _{0}^{r}{\sqrt {\left[{\frac {\mathrm {d} }{\mathrm {d} r}}x(r)(r=\rho )\right]^{2}+\left[{\frac {\mathrm {d} }{\mathrm {d} r}}y(r)(r=\rho )\right]^{2}}}\mathrm {d} \rho =}$

${\displaystyle =\int _{0}^{r}{\sqrt {\left[{\frac {\mathrm {d} }{\mathrm {d} \rho }}\rho {\sqrt {1+\rho ^{2}}}/{\sqrt {2}}\right]^{2}+\left[{\frac {\mathrm {d} }{\mathrm {d} \rho }}\rho {\sqrt {1-\rho ^{2}}}/{\sqrt {2}}\right]^{2}}}\mathrm {d} \rho =}$

${\displaystyle =\int _{0}^{r}{\sqrt {{\frac {(1+2\rho ^{2})^{2}}{2(1+\rho ^{2})}}+{\frac {(1-2\rho ^{2})^{2}}{2(1-\rho ^{2})}}}}\mathrm {d} \rho =\int _{0}^{r}{\frac {1}{\sqrt {1-\rho ^{4}}}}\mathrm {d} \rho }$

Gauß nannte diese Umkehrfunktion Sinus lemniscatus und bezeichnete sie mit ${\displaystyle \operatorname {sl} }$, also

${\displaystyle r=\operatorname {sl} \,s}$

Entsprechend definierte er den Cosinus lemniscatus ${\displaystyle \operatorname {cl} \,s=\operatorname {sl} \,({\tfrac {\varpi }{2}}-s)}$, wobei ${\displaystyle \varpi }$ die Länge des Halbbogens der Lemniskate ist, also

${\displaystyle \varpi =2\int _{0}^{1}{\frac {\mathrm {d} \,\rho }{\sqrt {1-\rho ^{4}}}}\approx 2{,}62205\ 75542\ 92119\ 81046\,48395\ 89891\ldots }$ (Folge A062539 in OEIS)

Gauß ließ sich bei diesen Bezeichnungen von der Analogie zu den Kreisfunktionen leiten, denn der Sinus ist die Umkehrfunktion des Integrals

${\displaystyle s(r)=\int _{0}^{r}{\frac {\mathrm {d} \,\rho }{\sqrt {1-\rho ^{2}}}},\qquad {\mbox{und}}\qquad 2\int _{0}^{1}{\frac {\mathrm {d} \,\rho }{\sqrt {1-\rho ^{2}}}}=\pi .}$

also ${\displaystyle r=\sin s}$ und ${\displaystyle \cos s=\sin({\tfrac {\pi }{2}}-s)}$. Seine weitere entscheidende Idee war es nun, die Funktionen ${\displaystyle \operatorname {sl} }$ und ${\displaystyle \operatorname {cl} }$ nicht nur für reelle Zahlen zu definieren, sondern sie ins Komplexe fortzusetzen. Er bewies dann die Periodizitätsrelationen

${\displaystyle \operatorname {sl} \,(s+2\varpi )=\operatorname {sl} \,s,\qquad \operatorname {sl} \,(s+2\mathrm {i} \varpi )=\operatorname {sl} \,s.}$

Im Gegensatz zum Sinus hat also der lemniskatische Sinus ${\displaystyle \operatorname {sl} }$ zwei Perioden ${\displaystyle 2\varpi }$ und ${\displaystyle 2\mathrm {i} \varpi }$, ebenso die Funktion ${\displaystyle \operatorname {cl} }$. Die lemniskatischen Funktionen sind also elliptisch. Carl Gustav Jacobi führte um 1830 die jacobischen elliptischen Funktionen ein und verallgemeinerte damit die beiden lemniskatischen Funktionen. Diese lassen sich auf folgende Weise durch die Jacobi-Funktionen mit dem Modul λ*(1) = 1/sqrt(2) ausdrücken:

${\displaystyle \operatorname {sl} \,(s)=\operatorname {sd} ({\sqrt {2}}s;1/{\sqrt {2}})/{\sqrt {2}}}$ und ${\displaystyle \operatorname {cl} \,(s)=\operatorname {cn} ({\sqrt {2}}s;1/{\sqrt {2}})}$

Somit sind der lemniskatische Sinus und der lemniskatische Cosinus auch über die Thetafunktionen auf folgende Weise^[1] definierbar:

${\displaystyle \operatorname {sl} \,(s)={\frac {\vartheta _{10}(\pi /2-\pi s/\varpi$ ;\operatorname {e} ^{-\pi })}{\vartheta _{01}(\pi /2-\pi s/\varpi ;\operatorname {e} ^{-\pi })}}} und ${\displaystyle \operatorname {cl} \,(s)={\frac {\vartheta _{10}(\pi s/\varpi$ ;\operatorname {e} ^{-\pi })}{\vartheta _{01}(\pi s/\varpi ;\operatorname {e} ^{-\pi })}}}

Definitionen

Die lemniskatischen Funktionen ${\displaystyle \operatorname {sl} }$ und ${\displaystyle \operatorname {cl} }$ können definiert werden als die Lösung des Anfangswertproblems

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sl} z={\bigl (}1+\operatorname {sl} ^{2}z{\bigr )}\operatorname {cl} z,\ {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cl} z=-{\bigl (}1+\operatorname {cl} ^{2}z{\bigr )}\operatorname {sl} z,\ \operatorname {sl} 0=0,\ \operatorname {cl} 0=1.}$

Äquivalent dazu ist die Definition als Umkehrfunktion zu einem elliptischen Integral:

${\displaystyle z=\int _{0}^{\operatorname {sl} z}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}=\int _{\operatorname {cl} z}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}.}$

Eine weitere Möglichkeit ist die Definition als Schwarz-Christoffel-Transformation von der Einheitskreisscheibe der komplexen Zahlenebene auf das Quadrat mit den Ecken ${\displaystyle {\tfrac {1}{2}}\varpi ,{\tfrac {1}{2}}\varpi \mathrm {i} ,-{\tfrac {1}{2}}\varpi ,-{\tfrac {1}{2}}\varpi \mathrm {i} }$.^[2] Die Funktionen können durch analytische Fortsetzung bzw. wiederholte Spiegelungen auf die gesamte Zahlenebene fortgesetzt werden.

Zum Vergleich die entsprechenden Definitionsmöglichkeiten für die Sinus- und die Kosinusfunktion:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\sin z=\cos z,\ {\frac {\mathrm {d} }{\mathrm {d} z}}\cos z=-\sin z,\ \sin 0=0,\ \cos 0=1,}$

${\displaystyle z=\int _{0}^{\sin z}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}=\int _{\cos z}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}.}$

Schwarz-Christoffel-Transformation der oberen Halbebene auf den Streifen mit Realteil zwischen ${\displaystyle -{\tfrac {1}{2}}\pi }$ und ${\displaystyle {\tfrac {1}{2}}\pi }$ und positivem Imaginärteil

Nullstellen, Pole und Symmetrieeigenschaften

${\displaystyle \operatorname {sl} }$ in der komplexen Zahlenebene.^[3] Aus der Zeichnung ist zu erkennen, dass die Perioden ${\displaystyle (1+\mathrm {i} )\varpi }$ und ${\displaystyle (1-\mathrm {i} )\varpi }$ „minimal“ sind in Bezug auf ihren Absolutbetrag.

Die lemniskatische Funktion ${\displaystyle \operatorname {cl} }$ ist eine gerade Funktion, dagegen ist ${\displaystyle \operatorname {sl} }$ eine ungerade Funktion.

${\displaystyle {\begin{aligned}\operatorname {cl} (-z)&=\operatorname {cl} z\\\operatorname {sl} (-z)&=-\operatorname {sl} z\end{aligned}}}$

Bei einer Translation um ${\displaystyle {\tfrac {1}{2}}\varpi }$ werden ${\displaystyle \operatorname {cl} }$ und ${\displaystyle \operatorname {sl} }$ vertauscht. Eine Translation um ${\displaystyle {\tfrac {1}{2}}\mathrm {i} \varpi }$ entspricht einer Vertauschung der Funktionen, verbunden mit einer Rotation um ${\displaystyle 90^{\circ }}$ und dem Übergang zum Kehrwert.

${\displaystyle {\begin{aligned}{\operatorname {cl} }\left(z\pm {\tfrac {1}{2}}\varpi \right)&=\mp \operatorname {sl} z,&{\operatorname {cl} }\left(z\pm {\tfrac {1}{2}}\mathrm {i} \varpi \right)&={\frac {\mp \mathrm {i} }{\operatorname {sl} z}}\\{\operatorname {sl} }\left(z\pm {\tfrac {1}{2}}\varpi \right)&=\pm \operatorname {cl} z,&{\operatorname {sl} }\left(z\pm {\tfrac {1}{2}}\mathrm {i} \varpi \right)&={\frac {\pm \mathrm {i} }{\operatorname {cl} z}}\end{aligned}}}$

Durch zweifache Anwendung einer solchen Translation, also durch eine Translation um ${\displaystyle \pm \varpi }$ bzw. ${\displaystyle \pm \mathrm {i} \varpi }$, erhält man jeweils die negierte Funktion. Es handelt sich also um Involutionen.

${\displaystyle {\begin{aligned}\operatorname {cl} (z+\varpi )&=\operatorname {cl} (z+\mathrm {i} \varpi )=-\operatorname {cl} z\\\operatorname {sl} (z+\varpi )&=\operatorname {sl} (z+\mathrm {i} \varpi )=-\operatorname {sl} z\end{aligned}}}$

Insgesamt sind die beiden Funktionen invariant unter einer Translation um das Produkt einer geraden gaußschen Zahl mit ${\displaystyle \varpi }$. Bei einer Verschiebung um ${\displaystyle (a+b\mathrm {i} )\varpi }$ mit ${\displaystyle a+b=2k}$ für ganze Zahlen ${\displaystyle a}$, ${\displaystyle b}$ und ${\displaystyle k}$ bleiben die Funktionswerte also unverändert.

${\displaystyle {\begin{aligned}{\operatorname {cl} }\left(z+(1+\mathrm {i} )\varpi \right)&={\operatorname {cl} }\left(z+(1-\mathrm {i} )\varpi \right)=\operatorname {cl} z\\{\operatorname {sl} }\left(z+(1+\mathrm {i} )\varpi \right)&={\operatorname {sl} }\left(z+(1-\mathrm {i} )\varpi \right)=\operatorname {sl} z\end{aligned}}}$

Dies macht die beiden Funktionen zu elliptischen Funktionen (doppelt periodisch und meromorph in der komplexen Zahlenebene) mit einem diagonal quadratischen Periodengitter, dessen Perioden ${\displaystyle (1+\mathrm {i} )\varpi }$ und ${\displaystyle (1-\mathrm {i} )\varpi }$ sind. Elliptische Funktionen mit einem quadratischen Periodengitter weisen ein höheres Maß an Symmetrie auf als beliebige elliptische Funktionen, entsprechend den Symmetrieeigenschaften des Quadrats.

Für Spiegelungen und Vierteldrehungen der Argumente einer lemniskatischen Funktion gibt es einfache Rechenausdrücke:

${\displaystyle {\begin{aligned}\operatorname {cl} {\bar {z}}&={\overline {\operatorname {cl} z}}\\\operatorname {sl} {\bar {z}}&={\overline {\operatorname {sl} z}}\\\operatorname {cl} \left(\mathrm {i} z\right)&={\frac {1}{\operatorname {cl} z}}\\\operatorname {sl} \left(\mathrm {i} z\right)&=\mathrm {i} \operatorname {sl} z\end{aligned}}}$

Die Funktion ${\displaystyle \operatorname {sl} }$ hat einfache Nullstellen bei den Produkten von gaußschen Zahlen mit ${\displaystyle \varpi }$, also bei komplexen Zahlen der Form ${\displaystyle a\varpi +b\varpi \mathrm {i} }$ mit ganzzahligem ${\displaystyle a}$ und ${\displaystyle b}$. Sie hat einfache Pole bei komplexen Zahlen der Form ${\displaystyle \left(a+{\tfrac {1}{2}}\right)\varpi +\left(b+{\tfrac {1}{2}}\right)\varpi \mathrm {i} }$. Die zugehörigen Residuen sind ${\displaystyle (-1)^{a-b+1}\mathrm {i} }$. Die Funktion ${\displaystyle \operatorname {cl} }$ ergibt sich durch Spiegelung und Verschiebung aus der Funktion ${\displaystyle \operatorname {sl} }$, denn es gilt ${\displaystyle \operatorname {cl} z={\operatorname {sl} }\left({\tfrac {1}{2}}\varpi -z\right)}$. Die ${\displaystyle \operatorname {cl} }$-Funktion hat Nullstellen für die Argumente ${\displaystyle \left(a+{\tfrac {1}{2}}\right)\varpi +b\varpi \mathrm {i} }$ und Pole für die Argumente ${\displaystyle a\varpi +\left(b+{\tfrac {1}{2}}\right)\varpi \mathrm {i} ,}$ mit den Residuen ${\displaystyle (-1)^{a-b}\mathrm {i} .}$

Die Aussage ${\displaystyle \operatorname {sl} z=\operatorname {sl} w}$ trifft genau dann zu, wenn ${\displaystyle z=(-1)^{m+n}w+(m+n\mathrm {i} )\varpi }$ für geeignete ${\displaystyle m,n\in \mathbb {Z} }$ gilt.

Algebraische Beziehungen

Folgende algebraische Beziehung gilt für die lemniskatischen Funktionen:

${\displaystyle [1+\operatorname {sl} (x)^{2}]\cdot [1+\operatorname {cl} (x)^{2}]=2}$

Die Additionstheoreme für die lemniskatischen Funktionen lauten wie folgt:

${\displaystyle \operatorname {sl} (a+b)={\frac {\operatorname {sl} (a)\cdot \operatorname {cl} (b)+\operatorname {cl} (a)\cdot \operatorname {sl} (b)}{1-\operatorname {sl} (a)\cdot \operatorname {cl} (a)\cdot \operatorname {sl} (b)\cdot \operatorname {cl} (b)}}}$

${\displaystyle \operatorname {cl} (a+b)={\frac {\operatorname {cl} (a)\cdot \operatorname {cl} (b)-\operatorname {sl} (a)\cdot \operatorname {sl} (b)}{1+\operatorname {sl} (a)\cdot \operatorname {cl} (a)\cdot \operatorname {sl} (b)\cdot \operatorname {cl} (b)}}}$

Alternative Darstellungen für die Additionstheoreme:

${\displaystyle \operatorname {sl} (a+b)={\frac {\operatorname {sl} (a)\cdot \operatorname {sl} '(b)+\operatorname {sl} '(a)\cdot \operatorname {sl} (b)}{1+\operatorname {sl} (a)^{2}\cdot \operatorname {sl} (b)^{2}}}}$

${\displaystyle \operatorname {cl} (a+b)={\frac {\operatorname {sl} '(a)\cdot \operatorname {sl} '(b)-2\cdot \operatorname {sl} (a)\cdot \operatorname {sl} (b)}{1+\operatorname {sl} (a)^{2}+\operatorname {sl} (b)^{2}-\operatorname {sl} (a)^{2}\cdot \operatorname {sl} (b)^{2}}}}$

Dabei ist die Ableitungsfunktion ${\displaystyle \operatorname {sl} '}$ (siehe unten) gegeben durch ${\displaystyle \operatorname {sl} '(x)=\operatorname {cl} (x)\cdot \left(1+(\operatorname {sl} (x))^{2}\right)}$.

Darstellung über den Arkustangens:

${\displaystyle \arctan[\operatorname {sl} (a+b)]=\arctan[\operatorname {sl} (a)\cdot \operatorname {cl} (b)]+\arctan[\operatorname {cl} (a)\cdot \operatorname {sl} (b)]}$

${\displaystyle \arctan[\operatorname {cl} (a+b)]=\arctan[\operatorname {cl} (a)\cdot \operatorname {cl} (b)]-\arctan[\operatorname {sl} (a)\cdot \operatorname {sl} (b)]}$

Für die Verdopplung gelten diese Formeln:

${\displaystyle \operatorname {sl} (2x)=2\,\operatorname {sl} (x)\operatorname {cl} (x){\frac {1+\operatorname {sl} (x)^{2}}{1+\operatorname {sl} (x)^{4}}}}$

${\displaystyle \operatorname {cl} (2x)={\frac {-1+2\,\operatorname {cl} (x)^{2}+\operatorname {cl} (x)^{4}}{1+2\,\operatorname {cl} (x)^{2}-\operatorname {cl} (x)^{4}}}}$

Dementsprechend gelten folgende Formeln für die Halbierung:

${\displaystyle \operatorname {sl} \left({\frac {x}{2}}\right)^{2}={\frac {1-\operatorname {cl} (x){\sqrt {1+\operatorname {sl} (x)^{2}}}}{{\sqrt {1+\operatorname {sl} (x)^{2}}}+1}}}$

${\displaystyle \operatorname {cl} \left({\frac {x}{2}}\right)^{2}={\frac {1+\operatorname {cl} (x){\sqrt {1+\operatorname {sl} (x)^{2}}}}{{\sqrt {1+\operatorname {sl} (x)^{2}}}+1}}}$

Für die Verdreifachung gilt Folgendes:

${\displaystyle \operatorname {sl} (3x)={\frac {3\,\operatorname {sl} (x)-6\,\operatorname {sl} (x)^{5}-\operatorname {sl} (x)^{9}}{1+6\,\operatorname {sl} (x)^{4}-3\,\operatorname {sl} (x)^{8}}}}$

Diese alternativen Darstellungen ermöglichen eine Umkehrung durch Lösen kubischer Gleichungen:

${\displaystyle \operatorname {sl} (3x)={\frac {{\sqrt[{4}]{27}}({\sqrt {3}}+1)y-{\sqrt {2}}y^{3}}{{\sqrt {2}}+{\sqrt[{4}]{27}}({\sqrt {3}}+1)y^{2}}}\left[y={\frac {{\sqrt[{4}]{3}}({\sqrt {3}}-1)\operatorname {sl} (x)+{\sqrt {2}}\operatorname {sl} (x)^{3}}{{\sqrt {2}}-{\sqrt[{4}]{3}}({\sqrt {3}}-1)\operatorname {sl} (x)^{2}}}\right]}$

${\displaystyle \operatorname {sl} (3x)={\frac {{\sqrt[{4}]{27}}({\sqrt {3}}+1)z+{\sqrt {2}}z^{3}}{{\sqrt {2}}-{\sqrt[{4}]{27}}({\sqrt {3}}+1)z^{2}}}\left[z={\frac {{\sqrt[{4}]{3}}({\sqrt {3}}-1)\operatorname {sl} (x)-{\sqrt {2}}\operatorname {sl} (x)^{3}}{{\sqrt {2}}+{\sqrt[{4}]{3}}({\sqrt {3}}-1)\operatorname {sl} (x)^{2}}}\right]}$

Der Cosinus Lemniscatus ergibt sich als negatives Analogon zum Sinus Lemniscatus:

${\displaystyle \operatorname {cl} (3x)={\frac {-3\,\operatorname {cl} (x)+6\,\operatorname {cl} (x)^{5}+\operatorname {cl} (x)^{9}}{1+6\,\operatorname {cl} (x)^{4}-3\,\operatorname {cl} (x)^{8}}}}$

Ableitungen

Die lemniskatischen Funktionen haben folgende Ableitungen:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {sl} (x)=\operatorname {cl} (x)\cdot [1+\operatorname {sl} (x)^{2}]}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {cl} (x)=-\operatorname {sl} (x)\cdot [1+\operatorname {cl} (x)^{2}]}$

Daraus folgt die Tatsache, dass die zweite Ableitung das negative doppelte vom Kubus ist.

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {sl} (x)=-2\cdot \operatorname {sl} (x)^{3}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {cl} (x)=-2\cdot \operatorname {cl} (x)^{3}}$

Über die Formeln der Ableitungen lassen sich ebenso die Stammfunktionen von Sinus Lemniscatus und Cosinus lemniscatus ermitteln.

${\displaystyle \operatorname {cl} (x)={\frac {\mathrm {d} }{\mathrm {d} x}}\arctan[\operatorname {sl} (x)]}$

${\displaystyle \operatorname {sl} (x)=-{\frac {\mathrm {d} }{\mathrm {d} x}}\arctan[\operatorname {cl} (x)]}$

Spezielle Werte

Einzelne Funktionswerte für die lemniskatischen Funktionen:

${\displaystyle \operatorname {sl} \left(0\right)=0=\operatorname {cl} \left({\frac {\varpi }{2}}\right)}$

${\displaystyle \operatorname {sl} \left({\frac {\varpi }{2}}\right)=1=\operatorname {cl} \left(0\right)}$

${\displaystyle \operatorname {sl} \left({\frac {\varpi }{4}}\right)={\sqrt {{\sqrt {2}}-1}}=\operatorname {cl} \left({\frac {\varpi }{4}}\right)}$

${\displaystyle \operatorname {sl} \left({\frac {\varpi }{6}}\right)={\frac {1}{2}}\cdot \left({\sqrt {3}}+1-{\sqrt[{4}]{12}}\right)=\operatorname {cl} \left({\frac {\varpi }{3}}\right)}$

${\displaystyle \operatorname {sl} \left({\frac {\varpi }{3}}\right)={\frac {\sqrt[{8}]{3}}{\sqrt[{4}]{2}}}\cdot {\sqrt {{\sqrt {3}}-1}}=\operatorname {cl} \left({\frac {\varpi }{6}}\right)}$

${\displaystyle \operatorname {sl} \left({\frac {\varpi }{8}}\right)={\sqrt {\left({\sqrt[{4}]{2}}-1\right)\cdot \left({\sqrt {2}}+1-{\sqrt {2+{\sqrt {2}}}}\right)}}=\operatorname {cl} \left({\frac {3\cdot \varpi }{8}}\right)}$

${\displaystyle \operatorname {sl} \left({\frac {3\cdot \varpi }{8}}\right)={\sqrt {\left({\sqrt[{4}]{2}}-1\right)\cdot \left({\sqrt {2}}+1+{\sqrt {2+{\sqrt {2}}}}\right)}}=\operatorname {cl} \left({\frac {\varpi }{8}}\right)}$

${\displaystyle \operatorname {sl} \left({\frac {\varpi }{5}}\right)={\frac {1}{2\cdot {\sqrt[{4}]{2}}}}\cdot ({\sqrt {5}}-1)\cdot {\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}-1}}}}=\operatorname {cl} \left({\frac {3\cdot \varpi }{10}}\right)}$

${\displaystyle \operatorname {sl} \left({\frac {2\cdot \varpi }{5}}\right)={\frac {1}{2\cdot {\sqrt[{4}]{2}}}}\cdot ({\sqrt {5}}-1)\cdot {\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}-1}}}}=\operatorname {cl} \left({\frac {\varpi }{10}}\right)}$

${\displaystyle \operatorname {sl} \left({\frac {\varpi }{10}}\right)={\frac {1}{2}}\cdot \left({\sqrt[{4}]{5}}-1\right)\cdot \left({\sqrt {{\sqrt {5}}+2}}-1\right)=\operatorname {cl} \left({\frac {2\cdot \varpi }{5}}\right)}$

${\displaystyle \operatorname {sl} \left({\frac {3\cdot \varpi }{10}}\right)={\frac {1}{2}}\cdot \left({\sqrt[{4}]{5}}-1\right)\cdot \left({\sqrt {{\sqrt {5}}+2}}+1\right)=\operatorname {cl} \left({\frac {\varpi }{5}}\right)}$

Weitere lemniskatische Funktionswerte in trigonometrischer Darstellung:

${\displaystyle \operatorname {sl} {\bigl (}{\tfrac {1}{12}}\varpi {\bigr )}={\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}}\sin \left({\tfrac {1}{24}}\pi \right)\right]\left({\sqrt[{4}]{2{\sqrt {3}}+3}}-1\right)=\operatorname {cl} {\bigl (}{\tfrac {5}{12}}\varpi {\bigr )}}$

${\displaystyle \operatorname {sl} {\bigl (}{\tfrac {5}{12}}\varpi {\bigr )}={\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}}\sin \left({\tfrac {1}{24}}\pi \right)\right]\left({\sqrt[{4}]{2{\sqrt {3}}+3}}+1\right)=\operatorname {cl} {\bigl (}{\tfrac {1}{12}}\varpi {\bigr )}}$

${\displaystyle \operatorname {sl} {\bigl (}{\tfrac {1}{14}}\varpi {\bigr )}=\tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {3}{14}}\pi )\cot({\tfrac {1}{28}}\pi )}}+\cos({\tfrac {1}{7}}\pi ){\bigr ]}{\bigr \}}=\operatorname {cl} {\bigl (}{\tfrac {3}{7}}\varpi {\bigr )}}$

${\displaystyle \operatorname {sl} {\bigl (}{\tfrac {3}{14}}\varpi {\bigr )}=\tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {1}{14}}\pi )\tan({\tfrac {5}{28}}\pi )}}+\sin({\tfrac {3}{14}}\pi ){\bigr ]}{\bigr \}}=\operatorname {cl} {\bigl (}{\tfrac {2}{7}}\varpi {\bigr )}}$

${\displaystyle \operatorname {sl} {\bigl (}{\tfrac {5}{14}}\varpi {\bigr )}=\tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\sin({\tfrac {1}{7}}\pi )\cot({\tfrac {3}{28}}\pi )}}+\sin({\tfrac {1}{14}}\pi ){\bigr ]}{\bigr \}}=\operatorname {cl} {\bigl (}{\tfrac {1}{7}}\varpi {\bigr )}}$

Reihenentwicklungen

Produktreihen nach Whittaker und Watson

Folgende Produktreihen für die lemniskatischen Funktionen konvergieren schnell:

${\displaystyle \operatorname {sl} (x)=2\exp \left(-{\tfrac {1}{4}}\pi \right)\sin(\pi x/\varpi )\prod _{k=1}^{\infty }{\frac {1-2\cos(2\pi x/\varpi )\exp(-2k\pi )+\exp(-4k\pi )}{1+2\cos(2\pi x/\varpi )\exp[-(2k-1)\pi ]+\exp[-(4k-2)\pi ]}}}$

${\displaystyle \operatorname {cl} (x)=2\exp \left(-{\tfrac {1}{4}}\pi \right)\cos(\pi x/\varpi )\prod _{k=1}^{\infty }{\frac {1+2\cos(2\pi x/\varpi )\exp(-2k\pi )+\exp(-4k\pi )}{1-2\cos(2\pi x/\varpi )\exp[-(2k-1)\pi ]+\exp[-(4k-2)\pi ]}}}$

Auf den Forschungsresultaten Edmund Taylor Whittaker und George Neville Watson^[4][5][6] basieren die nun genannten Produktreihen.

Trigonometrisch Hyperbolische Summenreihen

Diese Summen stellen schnell konvergierende Reihen zur numerischen Berechnung des lemniskatischen Sinus und Cosinus dar:^[7]

${\displaystyle \operatorname {sl} (x)={\frac {4\pi }{\varpi }}\sin \left({\frac {\pi x}{\varpi }}\right)\sum _{k=0}^{\infty }{\frac {(-1)^{k}\sinh[(k+1/2)\pi ]}{\cosh[(2k+1)\pi ]+\cos \left(2\pi x/\varpi \right)}},}$

${\displaystyle \operatorname {cl} (x)={\frac {4\pi }{\varpi }}\cos \left({\frac {\pi x}{\varpi }}\right)\sum _{k=0}^{\infty }{\frac {(-1)^{k}\sinh[(k+1/2)\pi ]}{\cosh[(2k+1)\pi ]-\cos(2\pi x/\varpi )}},}$

Hierbei verläuft die Präzision der Annäherung mit endlichem oberen Index ${\displaystyle m}$ wie ${\displaystyle 10^{-3m/2}}$ und somit linear.

Beide Reihen zeigen deutlich den Zusammenhang mit den Kreisfunktionen, indem die nach der lemniskatischen Form ausgestreckten Kreisfunktionen als Summanden in den genannten Differenzen gezeigt werden.

Basierend auf der Summendefinition der Jacobischen Zetafunktion können diese nicht alternierenden Summen aufgestellt werden:

${\displaystyle \tan \left\{{\frac {1}{2}}\arctan {\bigl [}\operatorname {sl} (x){\bigr ]}\right\}={\frac {4\pi }{\varpi }}\sin(\pi x/\varpi )\sum _{k=1}^{\infty }{\frac {\cosh[(2k-1)\pi ]}{\cosh[(2k-1)\pi ]^{2}-\cos(\pi x/\varpi )^{2}}}}$

${\displaystyle \tan \left\{{\frac {1}{2}}\arctan {\bigl [}\operatorname {cl} (x){\bigr ]}\right\}={\frac {4\pi }{\varpi }}\cos(\pi x/\varpi )\sum _{k=1}^{\infty }{\frac {\cosh[(2k-1)\pi ]}{\cosh[(2k-1)\pi ]^{2}-\sin(\pi x/\varpi )^{2}}}}$

Zusatzinformation:

Die Tangenshalbierungen von Sinus lemniscatus und Cosinus lemniscatus führen zu den Jacobi-Funktionen mit dem Modul λ*(4):

${\displaystyle \tan \left\{{\frac {1}{2}}\arctan {\bigl [}\operatorname {sl} (x){\bigr ]}\right\}=({\sqrt {2}}-1)\operatorname {sn} \left[{\tfrac {1}{2}}({\sqrt {2}}+1)x;({\sqrt {2}}-1)^{2}\right]}$

${\displaystyle \tan \left\{{\frac {1}{2}}\arctan {\bigl [}\operatorname {cl} (x){\bigr ]}\right\}=({\sqrt {2}}-1)\operatorname {cd} \left[{\tfrac {1}{2}}({\sqrt {2}}+1)x;({\sqrt {2}}-1)^{2}\right]}$

Rein Hyperbolische Summenreihen

Weitere Reihendarstellungen über alternierende Summen des Secans hyperbolicus lauten so:

${\displaystyle {\frac {\varpi }{\pi }}\operatorname {cl} (\varpi x)=\sum _{k=-\infty }^{\infty }(-1)^{k}\operatorname {sech} [\pi (k+x)]}$

${\displaystyle {\frac {\varpi }{\pi }}\operatorname {sl} (\varpi x)=\sum _{k=-\infty }^{\infty }(-1)^{k}\operatorname {sech} [\pi (k-{\frac {1}{2}}+x)]}$

Definition mit der Ramanujanschen Thetafunktion

Die Ramanujansche Thetafunktion hat diese Definition:

${\displaystyle \vartheta _{R}(v;w)=\sum _{n=-\infty }^{\infty }v^{n(n+1)/2}\,w^{n(n-1)/2}=\sum _{n=-\infty }^{\infty }v^{\bigtriangleup (n)}\,w^{\bigtriangleup (n-1)}}$

Der korrespondierende Ausdruck aus einer Summe mit dem Index Eins lautet demnach so:

${\displaystyle \vartheta _{R}(v;w)=1+v+w+\sum _{n=1}^{\infty }(vw)^{\bigtriangleup (n)}(v^{n+1}+w^{n+1})}$

So können darauf basierend folgende Identitäten hervorgebracht werden:

${\displaystyle 1+\tan {\biggl \{}{\frac {1}{8}}\pi -{\frac {1}{2}}\arctan {\bigl [}\mathrm {sl} (x){\bigr ]}{\biggr \}}={\sqrt {2}}\exp {\bigl (}-{\frac {x}{G}}{\bigr )}\,{\frac {\vartheta _{R}{\bigl [}\exp(x\div G-{\tfrac {1}{2}}\pi );\exp(-x\div G-{\tfrac {3}{2}}\pi ){\bigr ]}^{2}}{\vartheta _{R}{\bigl [}\exp(x\div G-{\tfrac {3}{2}}\pi );\exp(-x\div G-{\tfrac {1}{2}}\pi ){\bigr ]}^{2}}}}$

${\displaystyle 1+\tan {\biggl \{}{\frac {1}{8}}\pi -{\frac {1}{2}}\arctan {\bigl [}\mathrm {cl} (x){\bigr ]}{\biggr \}}={\sqrt {2}}\exp {\bigl (}{\frac {x}{G}}-{\frac {\pi }{2}}{\bigr )}\,{\frac {\vartheta _{R}{\bigl [}\exp(-x\div G);\exp(x\div G-2\pi ){\bigr ]}^{2}}{\vartheta _{R}{\bigl [}\exp(-x\div G-\pi );\exp(x\div G-\pi ){\bigr ]}^{2}}}}$

Noch viel schneller als die Reihen der vorherigen Abschnitte konvergieren somit folgende zwei Reihen für die lemniskatischen Funktionen, welche sich direkt aus den Formeln mit der Ramanujanschen Thetafunktion herleiten lassen:

${\displaystyle 1+\tan \left\{{\frac {1}{8}}\pi -{\frac {1}{2}}\arctan {\bigl [}\operatorname {sl} (x){\bigr ]}\right\}={\sqrt {2}}\,\left\{\sum _{k=-\infty }^{\infty }\exp \left[-\pi \left(k+{\frac {1}{4}}+{\frac {x}{2\varpi }}\right)^{2}\right]\right\}^{2}\left\{\sum _{k=-\infty }^{\infty }\exp \left[-\pi \left(k-{\frac {1}{4}}+{\frac {x}{2\varpi }}\right)^{2}\right]\right\}^{-2}}$

${\displaystyle 1+\tan \left\{{\frac {1}{8}}\pi -{\frac {1}{2}}\arctan {\bigl [}\operatorname {cl} (x){\bigr ]}\right\}={\sqrt {2}}\,\left\{\sum _{k=-\infty }^{\infty }\exp \left[-\pi \left(k+{\frac {1}{2}}+{\frac {x}{2\varpi }}\right)^{2}\right]\right\}^{2}\left\{\sum _{k=-\infty }^{\infty }\exp \left[-\pi \left(k+{\frac {x}{2\varpi }}\right)^{2}\right]\right\}^{-2}}$

Elliptische Lambdafunktion

Diejenigen elliptischen Module, welche die Lambda-Stern-Funktionswerte von den Doppelten der ungeraden natürlichen Zahlen^[8] sind, können vereinfacht mit dem Halbierungstheorem als Sinus-Lemniscatus-Quadrat dargestellt werden:

Muttermodul (Mm)	Tochtermodul (Tm)	Pythagoräisches Gegenstück vom Tm	Pythagoräisches Gegenstück vom Mm = Tangentielles Gegenstück vom Tm
${\displaystyle \lambda ^{*}({\tfrac {3}{2}})=\operatorname {cl} '[{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{3}}{\sqrt {3}})]}$	${\displaystyle \lambda ^{*}(6)=\operatorname {sl} [{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{3}}{\sqrt {3}})]^{2}}$	${\displaystyle \lambda ^{*}({\tfrac {1}{6}})=\operatorname {sl} '[{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{3}}{\sqrt {3}})]}$	${\displaystyle \lambda ^{*}({\tfrac {2}{3}})=\operatorname {cl} [{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{3}}{\sqrt {3}})]^{2}}$
${\displaystyle \lambda ^{*}({\tfrac {5}{2}})=\operatorname {cl} '[{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{3}})]}$	${\displaystyle \lambda ^{*}(10)=\operatorname {sl} [{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{3}})]^{2}}$	${\displaystyle \lambda ^{*}({\tfrac {1}{10}})=\operatorname {sl} '[{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{3}})]}$	${\displaystyle \lambda ^{*}({\tfrac {2}{5}})=\operatorname {cl} [{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{3}})]^{2}}$
${\displaystyle \lambda ^{*}({\tfrac {11}{2}})=\operatorname {cl} '[{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{33}}{\sqrt {11}})]}$	${\displaystyle \lambda ^{*}(22)=\operatorname {sl} [{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{33}}{\sqrt {11}})]^{2}}$	${\displaystyle \lambda ^{*}({\tfrac {1}{22}})=\operatorname {sl} '[{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{33}}{\sqrt {11}})]}$	${\displaystyle \lambda ^{*}({\tfrac {2}{11}})=\operatorname {cl} [{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{33}}{\sqrt {11}})]^{2}}$
${\displaystyle \lambda ^{*}({\tfrac {17}{2}})=\operatorname {cl} '\{{\tfrac {1}{2}}\operatorname {arcsl} [{\tfrac {1}{3}}({\sqrt {17}}-4)]\}}$	${\displaystyle \lambda ^{*}(34)=\operatorname {sl} \{{\tfrac {1}{2}}\operatorname {arcsl} [{\tfrac {1}{3}}({\sqrt {17}}-4)]\}^{2}}$	${\displaystyle \lambda ^{*}({\tfrac {1}{34}})=\operatorname {sl} '\{{\tfrac {1}{2}}\operatorname {arcsl} [{\tfrac {1}{3}}({\sqrt {17}}-4)]\}}$	${\displaystyle \lambda ^{*}({\tfrac {2}{17}})=\operatorname {cl} \{{\tfrac {1}{2}}\operatorname {arcsl} [{\tfrac {1}{3}}({\sqrt {17}}-4)]\}^{2}}$
${\displaystyle \lambda ^{*}({\tfrac {29}{2}})=\operatorname {cl} '[{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{99}})]}$	${\displaystyle \lambda ^{*}(58)=\operatorname {sl} [{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{99}})]^{2}}$	${\displaystyle \lambda ^{*}({\tfrac {1}{58}})=\operatorname {sl} '[{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{99}})]}$	${\displaystyle \lambda ^{*}({\tfrac {2}{29}})=\operatorname {cl} [{\tfrac {1}{2}}\operatorname {arcsl} ({\tfrac {1}{99}})]^{2}}$
${\displaystyle \lambda ^{*}({\tfrac {41}{2}})=\operatorname {cl} '\{{\tfrac {1}{2}}\operatorname {arcsl} [{\tfrac {1}{69}}(8{\sqrt {41}}-51)]\}}$	${\displaystyle \lambda ^{*}(82)=\operatorname {sl} \{{\tfrac {1}{2}}\operatorname {arcsl} [{\tfrac {1}{69}}(8{\sqrt {41}}-51)]\}^{2}}$	${\displaystyle \lambda ^{*}({\tfrac {1}{82}})=\operatorname {sl} '\{{\tfrac {1}{2}}\operatorname {arcsl} [{\tfrac {1}{69}}(8{\sqrt {41}}-51)]\}}$	${\displaystyle \lambda ^{*}({\tfrac {2}{41}})=\operatorname {cl} \{{\tfrac {1}{2}}\operatorname {arcsl} [{\tfrac {1}{69}}(8{\sqrt {41}}-51)]\}^{2}}$

Weitere Werte:

${\displaystyle \lambda ^{*}(14)=\operatorname {sl} \left\{{\tfrac {1}{2}}\operatorname {arcsl} \left[(8{\sqrt {2}}+11)^{-1/2}\right]\right\}^{2}}$

${\displaystyle \lambda ^{*}(26)=\operatorname {sl} \left\{{\tfrac {1}{2}}\operatorname {arcsl} \left[{\tfrac {1}{33}}\left(2{\sqrt[{3}]{132{\sqrt {78}}+837}}-2{\sqrt[{3}]{132{\sqrt {78}}-837}}-9\right)\right]\right\}^{2}}$

${\displaystyle \lambda ^{*}(38)=\operatorname {sl} \left\{{\tfrac {1}{2}}\operatorname {arcsl} \left[{\tfrac {1}{627}}{\sqrt {19}}\left(2{\sqrt[{3}]{3300{\sqrt {114}}+27323}}-2{\sqrt[{3}]{3300{\sqrt {114}}-27323}}-35\right)\right]\right\}^{2}}$

${\displaystyle \lambda ^{*}(46)=\operatorname {sl} \left\{{\tfrac {1}{2}}\operatorname {arcsl} \left[{\tfrac {1}{3}}(104{\sqrt {2}}+147)^{-1/2}\right]\right\}^{2}}$

${\displaystyle \lambda ^{*}(66)=\operatorname {sl} \left\{{\tfrac {1}{2}}\operatorname {arcsl} \left[\left({\tfrac {75}{2}}+{\tfrac {13}{2}}{\sqrt {33}}+{\tfrac {1}{2}}{\sqrt {1842{\sqrt {33}}+10578}}\right)^{-1}\right]\right\}^{2}}$

Zusammenhang mit anderen Funktionen

Die lemniskatischen Funktionen sind eng verwandt mit der weierstraßschen ℘-Funktion ${\displaystyle \wp (z;1,0)}$ („lemniskatischer Fall“), mit den Invarianten ${\displaystyle g_{2}=1}$ und ${\displaystyle g_{3}=0}$. Das zugehörige Gitter hat die Perioden ${\displaystyle \omega _{1}={\sqrt {2}}\varpi }$ und ${\displaystyle \omega _{2}=\mathrm {i} \omega _{1}=\mathrm {i} {\sqrt {2}}\varpi }$. Die entsprechenden Halbwerte sind ${\displaystyle e_{1}={\tfrac {1}{2}}}$, ${\displaystyle e_{2}=0}$, ${\displaystyle e_{3}=-{\tfrac {1}{2}}.}$

Der verwandte Fall einer weierstraßschen ℘-Funktion mit ${\displaystyle g_{2}=a}$, ${\displaystyle g_{3}=0}$ kann mit einer skalierenden Transformation behandelt werden, wobei auch komplexe Zahlen auftreten können. Falls man im Bereich der reellen Zahlen bleiben möchte, sind zwei Fälle zu betrachten, ${\displaystyle a>0}$ und ${\displaystyle a<0}$. Das Periodenparallelogramm ist entweder ein Quadrat oder eine Raute. Bei der weierstraßschen ℘-Funktion ${\displaystyle \wp (z;-1,0)}$ spricht man vom „pseudolemniskatischen Fall“.

Das Quadrat des lemniskatischen Sinus kann ausgedrückt werden durch

${\displaystyle \operatorname {sl} ^{2}z={\frac {1}{\wp (z;4,0)}}={\frac {i}{2\wp ((1-i)z;-1,0)}}={-2\wp }{\left({\sqrt {2}}z+(i-1){\frac {\varpi }{\sqrt {2}}};1,0\right)}.}$

wobei das zweite und dritte Argument von ${\displaystyle \wp }$ wieder die Invarianten ${\displaystyle g_{2}}$ und ${\displaystyle g_{3}}$ bezeichnen. Der lemniskatische Sinus selbst ist eine rationale Funktion bezüglich der weierstraßschen ℘-Funktion und deren Ableitung:^[9]

${\displaystyle \operatorname {sl} z=-2{\frac {\wp (z;-1,0)}{\wp '(z;-1,0)}}.}$

Die lemniskatischen Funktionen lassen sich auch durch jacobische elliptische Funktionen ausdrücken. Die jacobischen elliptischen Funktionen ${\displaystyle \operatorname {sn} }$ und ${\displaystyle \operatorname {cd} }$ mit positiv reellem elliptischem Modul haben ein „aufrechtes“ (also achsenparalleles) Rechtecksgitter. Alternativ dazu haben die Funktionen ${\displaystyle \operatorname {sn} }$ und ${\displaystyle \operatorname {cd} }$ mit dem Modul ${\displaystyle \mathrm {i} }$ (beziehungsweise ${\displaystyle \operatorname {sd} }$ und ${\displaystyle \operatorname {cn} }$ mit dem Modul ${\displaystyle 1/{\sqrt {2}}}$) ein quadratisches Periodengitter, das gegenüber den Achsen um ${\displaystyle 45^{\circ }}$ gedreht ist.^[10][11]

${\displaystyle \operatorname {sl} z=\operatorname {sn} (z;\mathrm {i} )=\operatorname {sc} (z;{\sqrt {2}})={{\tfrac {1}{\sqrt {2}}}\operatorname {sd} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right),}$

${\displaystyle \operatorname {cl} z=\operatorname {cd} (z;\mathrm {i} )=\operatorname {dn} (z;{\sqrt {2}})={\operatorname {cn} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right),}$

wobei das zweite Argument jeweils den elliptischen Modul ${\displaystyle k}$ angibt.

Siehe auch

• Lemniskatische Konstante
• Hyperbolisch lemniskatischer Sinus
• Lemniskatischer Arkussinus
• Jacobische elliptische Funktion

Literatur

• E. D. Solomentsev: Lemniscate functions. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org).
• Whittaker, E. T. and Watson, G. N.: A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990. p. 508

Weblinks

• Eric W. Weisstein: Lemniscate Function. In: MathWorld (englisch).