Top-Fragen
Zeitleiste
Chat
Kontext
Liouville-Funktion
mathematische Funktion Aus Wikipedia, der freien Enzyklopädie
Remove ads
Die Liouville-Funktion, benannt nach Joseph Liouville, ist eine multiplikative zahlentheoretische Funktion. Sie wird mit dem griechischen Buchstaben bezeichnet und ist wie folgt definiert:
dabei bezeichnet die Ordnung von , also die Anzahl seiner (nicht notwendigerweise verschiedenen) Primfaktoren.
Man definiert außerdem und .
Die ersten Werte (beginnend bei ) sind
Remove ads
Eigenschaften
Zusammenfassung
Kontext
Es gilt[3]
Die Liouville-Funktion ist verwandt mit der Möbius-Funktion durch[4]
Reihen
Die Dirichlet-Reihe der Liouville-Funktion lässt sich durch die riemannschen Zeta-Funktion ausdrücken:[5]
Ihre Lambert-Reihe ist gegeben durch
wobei die Jacobische Theta-Funktion bezeichnet.
Remove ads
Summen
Zusammenfassung
Kontext

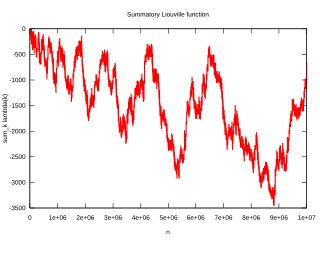
Es sei
Die Pólya-Vermutung besagt, es sei – wie die Grafiken rechts vermuten lassen – stets[6]
Diese Vermutung wurde mittlerweile widerlegt; das kleinste Gegenbeispiel ist . Es ist bisher allerdings nicht bekannt, ob sein Vorzeichen unendlich oft wechselt.
Eine verwandte Summe ist
Für diese wurde vermutet, sie sei für hinreichend große stets positiv; dies wurde 1958 von dem englischen Mathematiker Colin Brian Haselgrove widerlegt, wobei er zeigte, dass unendlich oft negative Werte annimmt.[7] Ein Beweis der Vermutung hätte die Richtigkeit der Riemannschen Vermutung zur Folge gehabt.[8]
Remove ads
Chowla-Vermutung
Eine Vermutung von Sarvadaman Chowla[9] besagt, dass für verschiedene natürliche Zahlen gilt:
(das heißt die Summe verschwindet asymptotisch mit , siehe Landau-Symbole). Die Vermutung ist offen für . Fortschritte erzielten 2015 Kaisa Matomäki, Maksym Radziwill und Terence Tao in Bezug auf eine gemittelte Version der Vermutung.[10] Die Vermutung lässt sich auch für die Möbiusfunktion statt der Liouvillefunktion formulieren.
Eine andere Formulierung der Vermutung ist, dass das Muster der Werte von für eine zufällig gewählte natürliche Zahl und beliebige asymptotisch für gleichverteilt ist.[11]
Remove ads
Weblinks
- Eric W. Weisstein: Liouville Function. In: MathWorld (englisch).
- A. F. Lavrik: Liouville function. In: Online Encyclopedia of Mathematics. (englisch)
- Kimberly Lloyd: Liouville function. Auf: PlanetMath.org. (englisch)
Einzelnachweise
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads





























