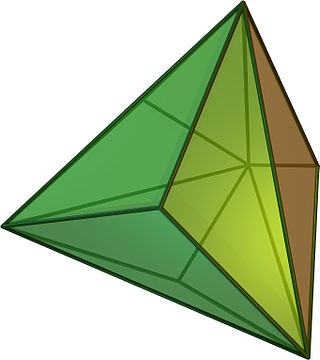
Triakistetraeder

Das Triakistetraeder ist ein konvexes Polyeder, das sich aus 12 gleichschenkligen Dreiecken zusammensetzt und zu den Catalanischen Körpern zählt. Es ist der duale Körper zum Tetraederstumpf und hat 8 Ecken sowie 18 Kanten.

Polyeder Triakistetraeder
3D-Ansicht eines Triakistetraeders (Animation)
Anzahl der Seitenflächen	12
Art der Seitenflächen	12 gleich­schenk­lige Dreiecke
Anzahl Ecken	8
Art der Ecken	4 × {3.3.3.3.3.3} + 4 × {3.3.3}
Anzahl Kanten	18
Symmetriegruppe	{{{Symmetriegruppe}}}
Schläfli-Symbol
dual zu	Tetraederstumpf
Körpernetz eines Triakistetraeders

Entstehung

Vierfach geschnittener Würfel

Drahtgittermodell eines Triakistetraeders

Werden auf alle 4 Begrenzungsflächen eines Tetraeders (mit Kantenlänge ${\displaystyle a}$) Pyramiden mit der Flankenlänge ${\displaystyle b}$ aufgesetzt, entsteht ein Triakistetraeder, sofern die Bedingung ${\displaystyle {\tfrac {a}{3}}{\sqrt {3}}<b<{\tfrac {a}{2}}{\sqrt {2}}}$ erfüllt ist.

• Für den zuvor genannten minimalen Wert von ${\displaystyle b}$ haben die aufgesetzten Pyramiden die Höhe 0, sodass lediglich das Tetraeder mit der Kantenlänge ${\displaystyle a}$ übrig bleibt.
• Das spezielle Triakistetraeder mit gleichen Flächenwinkeln entsteht, wenn ${\displaystyle b={\tfrac {3}{5}}a}$ ist.
• Nimmt ${\displaystyle b}$ den o. g. maximalen Wert an, entartet das Triakistetraeder zu einem Würfel mit der Kantenlänge ${\displaystyle b}$ (siehe Grafik links); dieser vierfach geschnittene Würfel – mit einem gedachten Tetraeder im Kern – ist topologisch gleichwertig zum Triakistetraeder.
• Überschreitet ${\displaystyle b}$ den maximalen Wert, so ist das Polyeder nicht mehr konvex und entartet zu einem Sternkörper.

Formeln

Allgemein ${\displaystyle {\tfrac {a}{3}}{\sqrt {3}}<b<{\tfrac {a}{2}}{\sqrt {2}}}$ Größen eines Triakistetraeders mit Kantenlängen a, b Volumen ${\displaystyle V={\frac {a^{2}}{12}}\left(a{\sqrt {2}}+4{\sqrt {3b^{2}-a^{2}}}\right)}$ Oberflächeninhalt ${\displaystyle A_{O}=3a{\sqrt {4b^{2}-a^{2}}}}$ Pyramidenhöhe ${\displaystyle k={\frac {1}{3}}{\sqrt {9b^{2}-3a^{2}}}}$ Inkugelradius ${\displaystyle \rho ={\frac {a}{12}}{\sqrt {\frac {48b^{2}-14a^{2}+8a{\sqrt {6b^{2}-2a^{2}}}}{4b^{2}-a^{2}}}}}$ Flächenwinkel  (über Kante a) ${\displaystyle \cos \,\alpha _{1}={\frac {5a^{2}-12b^{2}-8a{\sqrt {6b^{2}-2a^{2}}}}{9(4b^{2}-a^{2})}}}$ Flächenwinkel  (über Kante b) ${\displaystyle \cos \,\alpha _{2}={\frac {2b^{2}-a^{2}}{4b^{2}-a^{2}}}}$

Speziell ${\displaystyle b={\tfrac {3}{5}}a}$ Größen eines Triakistetraeders mit Kantenlänge a Volumen ${\displaystyle V={\frac {3}{20}}\,a^{3}{\sqrt {2}}}$ Oberflächeninhalt ${\displaystyle A_{O}={\frac {3}{5}}\,a^{2}{\sqrt {11}}}$ Pyramidenhöhe ${\displaystyle k={\frac {a}{15}}{\sqrt {6}}}$ Inkugelradius ${\displaystyle \rho ={\frac {3}{4}}\,a\,{\sqrt {\frac {2}{11}}}}$ Kantenkugelradius ${\displaystyle r={\frac {a}{4}}{\sqrt {2}}}$ Flächenwinkel  ≈ 129° 31′ 16″ ${\displaystyle \cos \,\alpha =-{\frac {7}{11}}}$ Sphärizität  ≈ 0,86439 ${\displaystyle \Psi ={\frac {\sqrt[{3}]{60\,\pi }}{2{\sqrt {11}}}}}$

Weblinks

Commons: Triakistetraeder – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Triakistetraeder – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Eric W. Weisstein: Triakistetraeder. In: MathWorld (englisch).
• Mineralienatlas:Triakistetraeder Interaktive Darstellung des Triakistetraeders im Mineralienatlas

Catalanische Körper

Triakistetraeder · Rhombendodekaeder · Tetrakishexaeder · Triakisoktaeder · Deltoidalikositetraeder · Pentagonikositetraeder · Rhombentriakontaeder · Hexakisoktaeder · Pentakisdodekaeder · Triakisikosaeder · Deltoidalhexakontaeder · Pentagonhexakontaeder · Hexakisikosaeder