Top Qs
Timeline
Chat
Perspective
Angular momentum
Conserved physical quantity; rotational analogue of linear momentum From Wikipedia, the free encyclopedia
Remove ads
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity – the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, flying discs,[1] rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes[2] form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it.
The three-dimensional angular momentum for a point particle is classically represented as a pseudovector r × p, the cross product of the particle's position vector r (relative to some origin) and its momentum vector; the latter is p = mv in Newtonian mechanics. Unlike linear momentum, angular momentum depends on where this origin is chosen, since the particle's position is measured from it.
Angular momentum is an extensive quantity; that is, the total angular momentum of any composite system is the sum of the angular momenta of its constituent parts. For a continuous rigid body or a fluid, the total angular momentum is the volume integral of angular momentum density (angular momentum per unit volume in the limit as volume shrinks to zero) over the entire body.
Similar to conservation of linear momentum, where it is conserved if there is no external force, angular momentum is conserved if there is no external torque. Torque can be defined as the rate of change of angular momentum, analogous to force. The net external torque on any system is always equal to the total torque on the system; the sum of all internal torques of any system is always 0 (this is the rotational analogue of Newton's third law of motion). Therefore, for a closed system (where there is no net external torque), the total torque on the system must be 0, which means that the total angular momentum of the system is constant.
The change in angular momentum for a particular interaction is called angular impulse, sometimes twirl.[3] Angular impulse is the angular analog of (linear) impulse.
Remove ads
Examples
Summarize
Perspective
The trivial case of the angular momentum of a body in an orbit is given by where is the mass of the orbiting object, is the orbit's frequency and is the orbit's radius.
The angular momentum of a uniform rigid sphere rotating around its axis, instead, is given by where is the sphere's mass, is the frequency of rotation and is the sphere's radius.
Thus, for example, the orbital angular momentum of the Earth with respect to the Sun is about 2.66 × 1040 kg⋅m2⋅s−1, while its rotational angular momentum is about 7.05 × 1033 kg⋅m2⋅s−1.
In the case of a uniform rigid sphere rotating around its axis, if, instead of its mass, its density is known, the angular momentum is given by where is the sphere's density, is the frequency of rotation and is the sphere's radius.
In the simplest case of a spinning disk, the angular momentum is given by[4] where is the disk's mass, is the frequency of rotation and is the disk's radius.
If instead the disk rotates about its diameter (e.g. coin toss), its angular momentum is given by[4]
Remove ads
Definition in classical mechanics
Summarize
Perspective
Just as for angular velocity, there are two special types of angular momentum of an object: the spin angular momentum is the angular momentum about the object's center of mass, while the orbital angular momentum is the angular momentum about a chosen center of rotation. The Earth has an orbital angular momentum by nature of revolving around the Sun, and a spin angular momentum by nature of its daily rotation around the polar axis. The total angular momentum is the sum of the spin and orbital angular momenta. In the case of the Earth the primary conserved quantity is the total angular momentum of the Solar System because angular momentum is exchanged to a small but important extent among the planets and the Sun. The orbital angular momentum vector of a point particle is always parallel and directly proportional to its orbital angular velocity vector ω, where the constant of proportionality depends on both the mass of the particle and its distance from origin. The spin angular momentum vector of a rigid body is proportional but not always parallel to the spin angular velocity vector Ω, making the constant of proportionality a second-rank tensor rather than a scalar.
Orbital angular momentum in two dimensions

Angular momentum is a vector quantity (more precisely, a pseudovector) that represents the product of a body's rotational inertia and rotational velocity (in radians/sec) about a particular axis. However, if the particle's trajectory lies in a single plane, it is sufficient to discard the vector nature of angular momentum, and treat it as a scalar (more precisely, a pseudoscalar).[5] Angular momentum can be considered a rotational analog of linear momentum. Thus, where linear momentum p is proportional to mass m and linear speed v, angular momentum L is proportional to moment of inertia I and angular speed ω measured in radians per second.[6]
Unlike mass, which depends only on amount of matter, moment of inertia depends also on the position of the axis of rotation and the distribution of the matter. Unlike linear velocity, which does not depend upon the choice of origin, orbital angular velocity is always measured with respect to a fixed origin. Therefore, strictly speaking, L should be referred to as the angular momentum relative to that center.[7]
In the case of circular motion of a single particle, we can use and to expand angular momentum as reducing to:
the product of the radius of rotation r and the linear momentum of the particle , where is the linear (tangential) speed.
This simple analysis can also apply to non-circular motion if one uses the component of the motion perpendicular to the radius vector: where is the perpendicular component of the motion. Expanding, rearranging, and reducing, angular momentum can also be expressed, where is the length of the moment arm, a line dropped perpendicularly from the origin onto the path of the particle. It is this definition, (length of moment arm) × (linear momentum), to which the term moment of momentum refers.[8]
Scalar angular momentum from Lagrangian mechanics
Another approach is to define angular momentum as the conjugate momentum (also called canonical momentum) of the angular coordinate expressed in the Lagrangian of the mechanical system. Consider a mechanical system with a mass constrained to move in a circle of radius in the absence of any external force field. The kinetic energy of the system is
And the potential energy is
Then the Lagrangian is
The generalized momentum "canonically conjugate to" the coordinate is defined by
Orbital angular momentum in three dimensions

To completely define orbital angular momentum in three dimensions, it is required to know the rate at which the position vector sweeps out an angle, the direction perpendicular to the instantaneous plane of angular displacement, and the mass involved, as well as how this mass is distributed in space.[9] By retaining this vector nature of angular momentum, the general nature of the equations is also retained, and can describe any sort of three-dimensional motion about the center of rotation – circular, linear, or otherwise. In vector notation, the orbital angular momentum of a point particle in motion about the origin can be expressed as: where
- is the moment of inertia for a point mass,
- is the orbital angular velocity of the particle about the origin,
- is the position vector of the particle relative to the origin, and ,
- is the linear velocity of the particle relative to the origin, and
- is the mass of the particle.
This can be expanded, reduced, and by the rules of vector algebra, rearranged: which is the cross product of the position vector and the linear momentum of the particle. By the definition of the cross product, the vector is perpendicular to both and . It is directed perpendicular to the plane of angular displacement, as indicated by the right-hand rule – so that the angular velocity is seen as counter-clockwise from the head of the vector. Conversely, the vector defines the plane in which and lie.
By defining a unit vector perpendicular to the plane of angular displacement, a scalar angular speed results, where and where is the perpendicular component of the motion, as above.
The two-dimensional scalar equations of the previous section can thus be given direction: and for circular motion, where all of the motion is perpendicular to the radius .
In the spherical coordinate system the angular momentum vector expresses as
Remove ads
Analogy to linear momentum
Summarize
Perspective
Angular momentum can be described as the rotational analog of linear momentum. Like linear momentum it involves elements of mass and displacement. Unlike linear momentum it also involves elements of position and shape.
Many problems in physics involve matter in motion about some certain point in space, be it in actual rotation about it, or simply moving past it, where it is desired to know what effect the moving matter has on the point—can it exert energy upon it or perform work about it? Energy, the ability to do work, can be stored in matter by setting it in motion—a combination of its inertia and its displacement. Inertia is measured by its mass, and displacement by its velocity. Their product, is the matter's momentum.[10] Referring this momentum to a central point introduces a complication: the momentum is not applied to the point directly. For instance, a particle of matter at the outer edge of a wheel is, in effect, at the end of a lever of the same length as the wheel's radius, its momentum turning the lever about the center point. This imaginary lever is known as the moment arm. It has the effect of multiplying the momentum's effort in proportion to its length, an effect known as a moment. Hence, the particle's momentum referred to a particular point, is the angular momentum, sometimes called, as here, the moment of momentum of the particle versus that particular center point. The equation combines a moment (a mass turning moment arm ) with a linear (straight-line equivalent) speed . Linear speed referred to the central point is simply the product of the distance and the angular speed versus the point: another moment. Hence, angular momentum contains a double moment: Simplifying slightly, the quantity is the particle's moment of inertia, sometimes called the second moment of mass. It is a measure of rotational inertia.[11]

The above analogy of the translational momentum and rotational momentum can be expressed in vector form:[citation needed]
- for linear motion
- for rotation
The direction of momentum is related to the direction of the velocity for linear movement. The direction of angular momentum is related to the angular velocity of the rotation.
Because moment of inertia is a crucial part of the spin angular momentum, the latter necessarily includes all of the complications of the former, which is calculated by multiplying elementary bits of the mass by the squares of their distances from the center of rotation.[12] Therefore, the total moment of inertia, and the angular momentum, is a complex function of the configuration of the matter about the center of rotation and the orientation of the rotation for the various bits.
For a rigid body, for instance a wheel or an asteroid, the orientation of rotation is simply the position of the rotation axis versus the matter of the body. It may or may not pass through the center of mass, or it may lie completely outside of the body. For the same body, angular momentum may take a different value for every possible axis about which rotation may take place.[13] It reaches a minimum when the axis passes through the center of mass.[14]
For a collection of objects revolving about a center, for instance all of the bodies of the Solar System, the orientations may be somewhat organized, as is the Solar System, with most of the bodies' axes lying close to the system's axis. Their orientations may also be completely random.
In brief, the more mass and the farther it is from the center of rotation (the longer the moment arm), the greater the moment of inertia, and therefore the greater the angular momentum for a given angular velocity. In many cases the moment of inertia, and hence the angular momentum, can be simplified by,[15] where is the radius of gyration, the distance from the axis at which the entire mass may be considered as concentrated.
Similarly, for a point mass the moment of inertia is defined as, where is the radius of the point mass from the center of rotation, and for any collection of particles as the sum,
Angular momentum's dependence on position and shape is reflected in its units versus linear momentum: kg⋅m2/s or N⋅m⋅s for angular momentum versus kg⋅m/s or N⋅s for linear momentum. When calculating angular momentum as the product of the moment of inertia times the angular velocity, the angular velocity must be expressed in radians per second, where the radian assumes the dimensionless value of unity. (When performing dimensional analysis, it may be productive to use orientational analysis which treats radians as a base unit, but this is not done in the International system of units). The units of angular momentum can be interpreted as torque⋅time. An object with angular momentum of L N⋅m⋅s can be reduced to zero angular velocity by an angular impulse of L N⋅m⋅s.[16][17]
The plane perpendicular to the axis of angular momentum and passing through the center of mass[18] is sometimes called the invariable plane, because the direction of the axis remains fixed if only the interactions of the bodies within the system, free from outside influences, are considered.[19] One such plane is the invariable plane of the Solar System.
Angular momentum and torque
Newton's second law of motion can be expressed mathematically, or force = mass × acceleration. The rotational equivalent for point particles may be derived as follows: which means that the torque (i.e. the time derivative of the angular momentum) is
Because the moment of inertia is , it follows that , and which, reduces to This is the rotational analog of Newton's second law. Note that the torque is not necessarily proportional or parallel to the angular acceleration (as one might expect). The reason for this is that the moment of inertia of a particle can change with time, something that cannot occur for ordinary mass.
Remove ads
Conservation of angular momentum
Summarize
Perspective

General considerations
A rotational analog of Newton's third law of motion might be written, "In a closed system, no torque can be exerted on any matter without the exertion on some other matter of an equal and opposite torque about the same axis."[20] Hence, angular momentum can be exchanged between objects in a closed system, but total angular momentum before and after an exchange remains constant (is conserved).[21]
Seen another way, a rotational analogue of Newton's first law of motion might be written, "A rigid body continues in a state of uniform rotation unless acted upon by an external influence."[20] Thus with no external influence to act upon it, the original angular momentum of the system remains constant.[22]
The conservation of angular momentum is used in analyzing central force motion. If the net force on some body is directed always toward some point, the center, then there is no torque on the body with respect to the center, as all of the force is directed along the radius vector, and none is perpendicular to the radius. Mathematically, torque because in this case and are parallel vectors. Therefore, the angular momentum of the body about the center is constant. This is the case with gravitational attraction in the orbits of planets and satellites, where the gravitational force is always directed toward the primary body and orbiting bodies conserve angular momentum by exchanging distance and velocity as they move about the primary. Central force motion is also used in the analysis of the Bohr model of the atom.
For a planet, angular momentum is distributed between the spin of the planet and its revolution in its orbit, and these are often exchanged by various mechanisms. The conservation of angular momentum in the Earth–Moon system results in the transfer of angular momentum from Earth to Moon, due to tidal torque the Moon exerts on the Earth. This in turn results in the slowing down of the rotation rate of Earth, at about 65.7 nanoseconds per day,[23] and in gradual increase of the radius of Moon's orbit, at about 3.82 centimeters per year.[24]
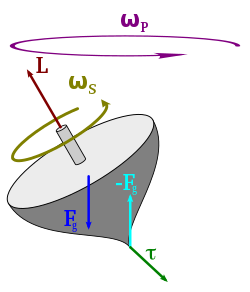
The conservation of angular momentum explains the angular acceleration of an ice skater as they bring their arms and legs close to the vertical axis of rotation. By bringing part of the mass of their body closer to the axis, they decrease their body's moment of inertia. Because angular momentum is the product of moment of inertia and angular velocity, if the angular momentum remains constant (is conserved), then the angular velocity (rotational speed) of the skater must increase.
The same phenomenon results in extremely fast spin of compact stars (like white dwarfs, neutron stars and black holes) when they are formed out of much larger and slower rotating stars.
Conservation is not always a full explanation for the dynamics of a system but is a key constraint. For example, a spinning top is subject to gravitational torque making it lean over and change the angular momentum about the nutation axis, but neglecting friction at the point of spinning contact, it has a conserved angular momentum about its spinning axis, and another about its precession axis. Also, in any planetary system, the planets, star(s), comets, and asteroids can all move in numerous complicated ways, but only so that the angular momentum of the system is conserved.
Noether's theorem states that every conservation law is associated with a symmetry (invariant) of the underlying physics. The symmetry associated with conservation of angular momentum is rotational invariance. The fact that the physics of a system is unchanged if it is rotated by any angle about an axis implies that angular momentum is conserved.[25]
Relation to Newton's second law of motion
While angular momentum total conservation can be understood separately from Newton's laws of motion as stemming from Noether's theorem in systems symmetric under rotations, it can also be understood simply as an efficient method of calculation of results that can also be otherwise arrived at directly from Newton's second law, together with laws governing the forces of nature (such as Newton's third law, Maxwell's equations and Lorentz force). Indeed, given initial conditions of position and velocity for every point, and the forces at such a condition, one may use Newton's second law to calculate the second derivative of position, and solving for this gives full information on the development of the physical system with time.[26] Note, however, that this is no longer true in quantum mechanics, due to the existence of particle spin, which is an angular momentum that cannot be described by the cumulative effect of point-like motions in space.
As an example, consider decreasing of the moment of inertia, e.g. when a figure skater is pulling in their hands, speeding up the circular motion. In terms of angular momentum conservation, we have, for angular momentum L, moment of inertia I and angular velocity ω:
Using this, we see that the change requires an energy of: so that a decrease in the moment of inertia requires investing energy.
This can be compared to the work done as calculated using Newton's laws. Each point in the rotating body is accelerating, at each point of time, with radial acceleration of:
Let us observe a point of mass m, whose position vector relative to the center of motion is perpendicular to the z-axis at a given point of time, and is at a distance z. The centripetal force on this point, keeping the circular motion, is:
Thus the work required for moving this point to a distance dz farther from the center of motion is:
For a non-pointlike body one must integrate over this, with m replaced by the mass density per unit z. This gives: which is exactly the energy required for keeping the angular momentum conserved.
Note, that the above calculation can also be performed per mass, using kinematics only. Thus the phenomena of figure skater accelerating tangential velocity while pulling their hands in, can be understood as follows in layman's language: The skater's palms are not moving in a straight line, so they are constantly accelerating inwards, but do not gain additional speed because the accelerating is always done when their motion inwards is zero. However, this is different when pulling the palms closer to the body: The acceleration due to rotation now increases the speed; but because of the rotation, the increase in speed does not translate to a significant speed inwards, but to an increase of the rotation speed.
Stationary-action principle
In classical mechanics it can be shown that the rotational invariance of action functionals implies conservation of angular momentum. The action is defined in classical physics as a functional of positions, often represented by the use of square brackets, and the final and initial times. It assumes the following form in cartesian coordinates:where the repeated indices indicate summation over the index. If the action is invariant of an infinitesimal transformation, it can be mathematically stated as: .
Under the transformation, , the action becomes: where we can employ the expansion of the terms up-to first order in : giving the following change in action:
Since all rotations can be expressed as matrix exponential of skew-symmetric matrices, i.e. as where is a skew-symmetric matrix and is angle of rotation, we can express the change of coordinates due to the rotation , up-to first order of infinitesimal angle of rotation, as:
Combining the equation of motion and rotational invariance of action, we get from the above equations that:Since this is true for any matrix that satisfies it results in the conservation of the following quantity: as . This corresponds to the conservation of angular momentum throughout the motion.[27]
Lagrangian formalism
In Lagrangian mechanics, angular momentum for rotation around a given axis, is the conjugate momentum of the generalized coordinate of the angle around the same axis. For example, , the angular momentum around the z axis, is: where is the Lagrangian and is the angle around the z axis.
Note that , the time derivative of the angle, is the angular velocity . Ordinarily, the Lagrangian depends on the angular velocity through the kinetic energy: The latter can be written by separating the velocity to its radial and tangential part, with the tangential part at the x-y plane, around the z-axis, being equal to: where the subscript i stands for the i-th body, and m, vT and ωz stand for mass, tangential velocity around the z-axis and angular velocity around that axis, respectively.
For a body that is not point-like, with density ρ, we have instead: where integration runs over the area of the body,[28] and Iz is the moment of inertia around the z-axis.
Thus, assuming the potential energy does not depend on ωz (this assumption may fail for electromagnetic systems), we have the angular momentum of the ith object:
We have thus far rotated each object by a separate angle; we may also define an overall angle θz by which we rotate the whole system, thus rotating also each object around the z-axis, and have the overall angular momentum:
From Euler–Lagrange equations it then follows that:
Since the lagrangian is dependent upon the angles of the object only through the potential, we have: which is the torque on the ith object.
Suppose the system is invariant to rotations, so that the potential is independent of an overall rotation by the angle θz (thus it may depend on the angles of objects only through their differences, in the form ). We therefore get for the total angular momentum: And thus the angular momentum around the z-axis is conserved.
This analysis can be repeated separately for each axis, giving conversation of the angular momentum vector. However, the angles around the three axes cannot be treated simultaneously as generalized coordinates, since they are not independent; in particular, two angles per point suffice to determine its position. While it is true that in the case of a rigid body, fully describing it requires, in addition to three translational degrees of freedom, also specification of three rotational degrees of freedom; however these cannot be defined as rotations around the Cartesian axes (see Euler angles). This caveat is reflected in quantum mechanics in the non-trivial commutation relations of the different components of the angular momentum operator.
Hamiltonian formalism
Equivalently, in Hamiltonian mechanics the Hamiltonian can be described as a function of the angular momentum. As before, the part of the kinetic energy related to rotation around the z-axis for the ith object is: which is analogous to the energy dependence upon momentum along the z-axis, .
Hamilton's equations relate the angle around the z-axis to its conjugate momentum, the angular momentum around the same axis:
The first equation gives
And so we get the same results as in the Lagrangian formalism.
Note, that for combining all axes together, we write the kinetic energy as: where pr is the momentum in the radial direction, and the moment of inertia is a 3-dimensional matrix; bold letters stand for 3-dimensional vectors.
For point-like bodies we have:
This form of the kinetic energy part of the Hamiltonian is useful in analyzing central potential problems, and is easily transformed to a quantum mechanical work frame (e.g. in the hydrogen atom problem).
Remove ads
Angular momentum in orbital mechanics
Summarize
Perspective
While in classical mechanics the language of angular momentum can be replaced by Newton's laws of motion, it is particularly useful for motion in central potential such as planetary motion in the solar system. Thus, the orbit of a planet in the solar system is defined by its energy, angular momentum and angles of the orbit major axis relative to a coordinate frame.
In astrodynamics and celestial mechanics, a quantity closely related to angular momentum is defined as[29] called specific angular momentum. Note that Mass is often unimportant in orbital mechanics calculations, because motion of a body is determined by gravity. The primary body of the system is often so much larger than any bodies in motion about it that the gravitational effect of the smaller bodies on it can be neglected; it maintains, in effect, constant velocity. The motion of all bodies is affected by its gravity in the same way, regardless of mass, and therefore all move approximately the same way under the same conditions.
Remove ads
Solid bodies
Summarize
Perspective
Angular momentum is also an extremely useful concept for describing rotating rigid bodies such as a gyroscope or a rocky planet. For a continuous mass distribution with density function ρ(r), a differential volume element dV with position vector r within the mass has a mass element dm = ρ(r)dV. Therefore, the infinitesimal angular momentum of this element is: and integrating this differential over the volume of the entire mass gives its total angular momentum:
In the derivation which follows, integrals similar to this can replace the sums for the case of continuous mass.
Collection of particles

For a collection of particles in motion about an arbitrary origin, it is informative to develop the equation of angular momentum by resolving their motion into components about their own center of mass and about the origin. Given,
- is the mass of particle ,
- is the position vector of particle w.r.t. the origin,
- is the velocity of particle w.r.t. the origin,
- is the position vector of the center of mass w.r.t. the origin,
- is the velocity of the center of mass w.r.t. the origin,
- is the position vector of particle w.r.t. the center of mass,
- is the velocity of particle w.r.t. the center of mass,
The total mass of the particles is simply their sum,
The position vector of the center of mass is defined by,[30]
By inspection,
- and
The total angular momentum of the collection of particles is the sum of the angular momentum of each particle,
(1)
Expanding ,
Expanding ,
It can be shown that (see sidebar),
|
Prove that which, by the definition of the center of mass, is and similarly for |
- and
therefore the second and third terms vanish,
The first term can be rearranged,
and total angular momentum for the collection of particles is finally,[31]
(2)
The first term is the angular momentum of the center of mass relative to the origin. Similar to § Single particle, below, it is the angular momentum of one particle of mass M at the center of mass moving with velocity V. The second term is the angular momentum of the particles moving relative to the center of mass, similar to § Fixed center of mass, below. The result is general—the motion of the particles is not restricted to rotation or revolution about the origin or center of mass. The particles need not be individual masses, but can be elements of a continuous distribution, such as a solid body.
Rearranging equation (2) by vector identities, multiplying both terms by "one", and grouping appropriately, gives the total angular momentum of the system of particles in terms of moment of inertia and angular velocity ,
(3)
Single particle case
In the case of a single particle moving about the arbitrary origin, and equations (2) and (3) for total angular momentum reduce to,
Case of a fixed center of mass
For the case of the center of mass fixed in space with respect to the origin, and equations (2) and (3) for total angular momentum reduce to,
Remove ads
Angular momentum in general relativity
Summarize
Perspective

In modern (20th century) theoretical physics, angular momentum (not including any intrinsic angular momentum – see below) is described using a different formalism, instead of a classical pseudovector. In this formalism, angular momentum is the 2-form Noether charge associated with rotational invariance. As a result, angular momentum is generally not conserved locally for general curved spacetimes, unless they have rotational symmetry;[32] whereas globally the notion of angular momentum itself only makes sense if the spacetime is asymptotically flat.[33] If the spacetime is only axially symmetric like for the Kerr metric, the total angular momentum is not conserved but is conserved which is related to the invariance of rotating around the symmetry-axis, where note that where is the metric, is the rest mass, is the four-velocity, and is the four-position in spherical coordinates.
In classical mechanics, the angular momentum of a particle can be reinterpreted as a plane element: in which the exterior product (∧) replaces the cross product (×) (these products have similar characteristics but are nonequivalent). This has the advantage of a clearer geometric interpretation as a plane element, defined using the vectors x and p, and the expression is true in any number of dimensions. In Cartesian coordinates: or more compactly in index notation:
The angular velocity can also be defined as an anti-symmetric second order tensor, with components ωij. The relation between the two anti-symmetric tensors is given by the moment of inertia which must now be a fourth order tensor:[34]
Again, this equation in L and ω as tensors is true in any number of dimensions. This equation also appears in the geometric algebra formalism, in which L and ω are bivectors, and the moment of inertia is a mapping between them.
In relativistic mechanics, the relativistic angular momentum of a particle is expressed as an anti-symmetric tensor of second order: in terms of four-vectors, namely the four-position X and the four-momentum P, and absorbs the above L together with the moment of mass, i.e., the product of the relativistic mass of the particle and its center of mass, which can be thought of as describing the motion of its center of mass, since mass–energy is conserved.
In each of the above cases, for a system of particles the total angular momentum is just the sum of the individual particle angular momenta, and the center of mass is for the system.
Remove ads
Angular momentum in quantum mechanics
Summarize
Perspective
In quantum mechanics, angular momentum (like other quantities) is expressed as an operator, and its one-dimensional projections have quantized eigenvalues. Angular momentum is subject to the Heisenberg uncertainty principle, implying that at any time, only one projection (also called "component") can be measured with definite precision; the other two then remain uncertain. Because of this, the axis of rotation of a quantum particle is undefined. Quantum particles do possess a type of non-orbital angular momentum called "spin", but this angular momentum does not correspond to a spinning motion.[35] In relativistic quantum mechanics the above relativistic definition becomes a tensorial operator.
Spin, orbital, and total angular momentum

- Left: "spin" angular momentum S is really orbital angular momentum of the object at every point.
- Right: extrinsic orbital angular momentum L about an axis.
- Top: the moment of inertia tensor I and angular velocity ω (L is not always parallel to ω).[36]
- Bottom: momentum p and its radial position r from the axis. The total angular momentum (spin plus orbital) is J. For a quantum particle the interpretations are different; particle spin does not have the above interpretation.
The classical definition of angular momentum as can be carried over to quantum mechanics, by reinterpreting r as the quantum position operator and p as the quantum momentum operator. L is then an operator, specifically called the orbital angular momentum operator. The components of the angular momentum operator satisfy the commutation relations of the Lie algebra SO(3).[37] Indeed, these operators are precisely the infinitesimal action of the rotation group on the quantum Hilbert space.[38] (See also the discussion below of the angular momentum operators as the generators of rotations.)
However, in quantum physics, there is another type of angular momentum, called spin angular momentum, represented by the spin operator S. Spin is often depicted as a particle literally spinning around an axis, but this is a misleading and inaccurate picture: spin is an intrinsic property of a particle, unrelated to any sort of motion in space and fundamentally different from orbital angular momentum. All elementary particles have a characteristic spin (possibly zero),[39] and almost all elementary particles have nonzero spin.[40] For example electrons have "spin 1/2" (this actually means "spin ħ/2"), photons have "spin 1" (this actually means "spin ħ"), and pi-mesons have spin 0.[41]
Finally, there is total angular momentum J, which combines both the spin and orbital angular momentum of all particles and fields. (For one particle, J = L + S.) Conservation of angular momentum applies to J, but not to L or S; for example, the spin–orbit interaction allows angular momentum to transfer back and forth between L and S, with the total remaining constant. Electrons and photons need not have integer-based values for total angular momentum, but can also have half-integer values.[42]
In molecules the total angular momentum F is the sum of the rovibronic (orbital) angular momentum N, the electron spin angular momentum S, and the nuclear spin angular momentum I. For electronic singlet states the rovibronic angular momentum is denoted J rather than N. As explained by Van Vleck,[43] the components of the molecular rovibronic angular momentum referred to molecule-fixed axes have different commutation relations from those for the components about space-fixed axes.
Quantization
In quantum mechanics, angular momentum is quantized – that is, it cannot vary continuously, but only in "quantum leaps" between certain allowed values. For any system, the following restrictions on measurement results apply, where is the reduced Planck constant and is any Euclidean vector such as x, y, or z:
| If you measure... | The result can be... |
| or | |
| , where | |
| or | , where |

The reduced Planck constant is tiny by everyday standards, about 10−34 J s, and therefore this quantization does not noticeably affect the angular momentum of macroscopic objects. However, it is very important in the microscopic world. For example, the structure of electron shells and subshells in chemistry is significantly affected by the quantization of angular momentum.
Quantization of angular momentum was first postulated by Niels Bohr in his model of the atom and was later predicted by Erwin Schrödinger in his Schrödinger equation.
Uncertainty
In the definition , six operators are involved: The position operators , , , and the momentum operators , , . However, the Heisenberg uncertainty principle tells us that it is not possible for all six of these quantities to be known simultaneously with arbitrary precision. Therefore, there are limits to what can be known or measured about a particle's angular momentum. It turns out that the best that one can do is to simultaneously measure both the angular momentum vector's magnitude and its component along one axis.
The uncertainty is closely related to the fact that different components of an angular momentum operator do not commute, for example . (For the precise commutation relations, see angular momentum operator.)
Total angular momentum as generator of rotations
As mentioned above, orbital angular momentum L is defined as in classical mechanics: , but total angular momentum J is defined in a different, more basic way: J is defined as the "generator of rotations".[44] More specifically, J is defined so that the operator is the rotation operator that takes any system and rotates it by angle about the axis . (The "exp" in the formula refers to operator exponential.) To put this the other way around, whatever our quantum Hilbert space is, we expect that the rotation group SO(3) will act on it. There is then an associated action of the Lie algebra so(3) of SO(3); the operators describing the action of so(3) on our Hilbert space are the (total) angular momentum operators.
The relationship between the angular momentum operator and the rotation operators is the same as the relationship between Lie algebras and Lie groups in mathematics. The close relationship between angular momentum and rotations is reflected in Noether's theorem that proves that angular momentum is conserved whenever the laws of physics are rotationally invariant.
Remove ads
Angular momentum in electrodynamics
Summarize
Perspective
When describing the motion of a charged particle in an electromagnetic field, the canonical momentum P (derived from the Lagrangian for this system) is not gauge invariant. As a consequence, the canonical angular momentum L = r × P is not gauge invariant either. Instead, the momentum that is physical, the so-called kinetic momentum (used throughout this article), is (in SI units) where e is the electric charge of the particle and A the magnetic vector potential of the electromagnetic field. The gauge-invariant angular momentum, that is kinetic angular momentum, is given by
The interplay with quantum mechanics is discussed further in the article on canonical commutation relations.
Angular momentum in optics
In classical Maxwell electrodynamics the Poynting vector is a linear momentum density of electromagnetic field.[45]
The angular momentum density vector is given by a vector product as in classical mechanics:[46]
The above identities are valid locally, i.e. in each space point in a given moment .
Remove ads
Angular momentum in nature and the cosmos
Summarize
Perspective
Tropical cyclones and other related weather phenomena involve conservation of angular momentum in order to explain the dynamics. Winds revolve slowly around low pressure systems, mainly due to the coriolis effect. If the low pressure intensifies and the slowly circulating air is drawn toward the center, the molecules must speed up in order to conserve angular momentum. By the time they reach the center, the speeds become destructive.[2]
Johannes Kepler determined the laws of planetary motion without knowledge of conservation of momentum. However, not long after his discovery their derivation was determined from conservation of angular momentum. Planets move more slowly the further they are out in their elliptical orbits, which is explained intuitively by the fact that orbital angular momentum is proportional to the radius of the orbit. Since the mass does not change and the angular momentum is conserved, the velocity drops.
Tidal acceleration is an effect of the tidal forces between an orbiting natural satellite (e.g. the Moon) and the primary planet that it orbits (e.g. Earth). The gravitational torque between the Moon and the tidal bulge of Earth causes the Moon to be constantly promoted to a slightly higher orbit (~3.8 cm per year) and Earth to be decelerated (by −25.858 ± 0.003″/cy²) in its rotation (the length of the day increases by ~1.7 ms per century, +2.3 ms from tidal effect and −0.6 ms from post-glacial rebound). The Earth loses angular momentum which is transferred to the Moon such that the overall angular momentum is conserved.
Remove ads
Angular momentum in engineering and technology
Examples of using conservation of angular momentum for practical advantage are abundant. In engines such as steam engines or internal combustion engines, a flywheel is needed to efficiently convert the lateral motion of the pistons to rotational motion.
Inertial navigation systems explicitly use the fact that angular momentum is conserved with respect to the inertial frame of space. Inertial navigation is what enables submarine trips under the polar ice cap, but are also crucial to all forms of modern navigation.
Rifled bullets use the stability provided by conservation of angular momentum to be more true in their trajectory. The invention of rifled firearms and cannons gave their users significant strategic advantage in battle, and thus were a technological turning point in history.
History
Summarize
Perspective
Isaac Newton, in the Principia, hinted at angular momentum in his examples of the first law of motion,
A top, whose parts by their cohesion are perpetually drawn aside from rectilinear motions, does not cease its rotation, otherwise than as it is retarded by the air. The greater bodies of the planets and comets, meeting with less resistance in more free spaces, preserve their motions both progressive and circular for a much longer time.[47]
He did not further investigate angular momentum directly in the Principia, saying:
From such kind of reflexions also sometimes arise the circular motions of bodies about their own centers. But these are cases which I do not consider in what follows; and it would be too tedious to demonstrate every particular that relates to this subject.[48]
However, his geometric proof of the law of areas is an outstanding example of Newton's genius, and indirectly proves angular momentum conservation in the case of a central force.
Law of Areas
Newton's derivation
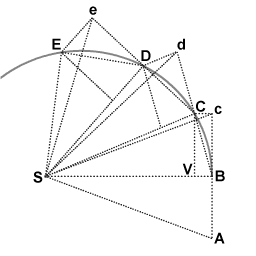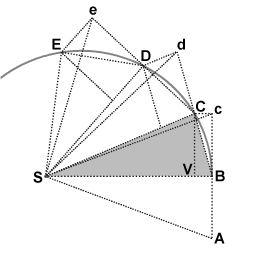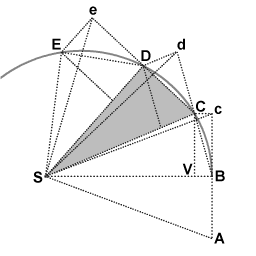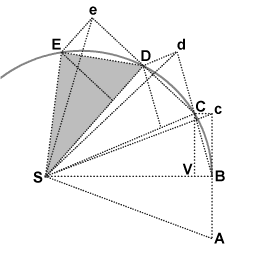
As a planet orbits the Sun, the line between the Sun and the planet sweeps out equal areas in equal intervals of time. This had been known since Kepler expounded his second law of planetary motion. Newton derived a unique geometric proof, and went on to show that the attractive force of the Sun's gravity was the cause of all of Kepler's laws.
During the first interval of time, an object is in motion from point A to point B. Undisturbed, it would continue to point c during the second interval. When the object arrives at B, it receives an impulse directed toward point S. The impulse gives it a small added velocity toward S, such that if this were its only velocity, it would move from B to V during the second interval. By the rules of velocity composition, these two velocities add, and point C is found by construction of parallelogram BcCV. Thus the object's path is deflected by the impulse so that it arrives at point C at the end of the second interval. Because the triangles SBc and SBC have the same base SB and the same height Bc or VC, they have the same area. By symmetry, triangle SBc also has the same area as triangle SAB, therefore the object has swept out equal areas SAB and SBC in equal times.
At point C, the object receives another impulse toward S, again deflecting its path during the third interval from d to D. Thus it continues to E and beyond, the triangles SAB, SBc, SBC, SCd, SCD, SDe, SDE all having the same area. Allowing the time intervals to become ever smaller, the path ABCDE approaches indefinitely close to a continuous curve.
Note that because this derivation is geometric, and no specific force is applied, it proves a more general law than Kepler's second law of planetary motion. It shows that the Law of Areas applies to any central force, attractive or repulsive, continuous or non-continuous, or zero.
Conservation of angular momentum in the law of areas
The proportionality of angular momentum to the area swept out by a moving object can be understood by realizing that the bases of the triangles, that is, the lines from S to the object, are equivalent to the radius r, and that the heights of the triangles are proportional to the perpendicular component of velocity v⊥. Hence, if the area swept per unit time is constant, then by the triangular area formula 1/2(base)(height), the product (base)(height) and therefore the product rv⊥ are constant: if r and the base length are decreased, v⊥ and height must increase proportionally. Mass is constant, therefore angular momentum rmv⊥ is conserved by this exchange of distance and velocity.
In the case of triangle SBC, area is equal to 1/2(SB)(VC). Wherever C is eventually located due to the impulse applied at B, the product (SB)(VC), and therefore rmv⊥ remain constant. Similarly so for each of the triangles.
Another areal proof of conservation of angular momentum for any central force uses Mamikon's sweeping tangents theorem.[49][50]
After Newton
Leonhard Euler, Daniel Bernoulli, and Patrick d'Arcy all understood angular momentum in terms of conservation of areal velocity, a result of their analysis of Kepler's second law of planetary motion. It is unlikely that they realized the implications for ordinary rotating matter.[51]
In 1736 Euler, like Newton, touched on some of the equations of angular momentum in his Mechanica without further developing them.[52]
Bernoulli wrote in a 1744 letter of a "moment of rotational motion", possibly the first conception of angular momentum as we now understand it.[53]
In 1799, Pierre-Simon Laplace first realized that a fixed plane was associated with rotation—his invariable plane.
Louis Poinsot in 1803 began representing rotations as a line segment perpendicular to the rotation, and elaborated on the "conservation of moments".
In 1852 Léon Foucault used a gyroscope in an experiment to display the Earth's rotation.
William J. M. Rankine's 1858 Manual of Applied Mechanics defined angular momentum in the modern sense for the first time:
... a line whose length is proportional to the magnitude of the angular momentum, and whose direction is perpendicular to the plane of motion of the body and of the fixed point, and such, that when the motion of the body is viewed from the extremity of the line, the radius-vector of the body seems to have right-handed rotation.
In an 1872 edition of the same book, Rankine stated that "The term angular momentum was introduced by Mr. Hayward,"[54] probably referring to R.B. Hayward's article On a Direct Method of estimating Velocities, Accelerations, and all similar Quantities with respect to Axes moveable in any manner in Space with Applications,[55] which was introduced in 1856, and published in 1864. Rankine was mistaken, as numerous publications feature the term starting in the late 18th to early 19th centuries.[56] However, Hayward's article apparently was the first use of the term and the concept seen by much of the English-speaking world. Before this, angular momentum was typically referred to as "momentum of rotation" in English.[57]
See also
- Absolute angular momentum
- Angular momentum coupling
- Angular momentum of light
- Angular momentum diagrams (quantum mechanics)
- Chaotic rotation
- Clebsch–Gordan coefficients
- Linear-rotational analogs
- Orders of magnitude (angular momentum)
- Pauli–Lubanski pseudovector
- Relativistic angular momentum
- Rigid rotor
- Rotational energy
- Specific relative angular momentum
- Yrast
References
Further reading
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads















































































![{\displaystyle S\left([x_{i}];t_{1},t_{2}\right)\equiv \int _{t_{1}}^{t_{2}}dt\left({\frac {1}{2}}m{\frac {dx_{i}}{dt}}\ {\frac {dx_{i}}{dt}}-V(x_{i})\right)}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0a1a0a77886ae741be2679b9b7123e90de2e3ae9)
![{\textstyle \delta S=S\left([x_{i}+\delta x_{i}];t_{1},t_{2}\right)-S\left([x_{i}];t_{1},t_{2}\right)=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/560e494d7450ac05174984f59efb1377447616e5)

![{\displaystyle S\left([x_{i}+\delta x_{i}];t_{1},t_{2}\right)=\!\int _{t_{1}}^{t_{2}}dt\left({\frac {1}{2}}m{\frac {d(x_{i}+\delta x_{i})}{dt}}{\frac {d(x_{i}+\delta x_{i})}{dt}}-V(x_{i}+\delta x_{i})\right)}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b6cea9bc1b2c5c3fe5c29911ab7cedd3b088354b)


![{\displaystyle S[x_{i}+\delta x_{i}]\simeq S[x_{i}]+\int _{t_{1}}^{t_{2}}dt\,\delta x_{i}\left(-{\frac {\partial V}{\partial x_{i}}}-m{\frac {d^{2}x_{i}}{dt^{2}}}\right)+m\int _{t_{1}}^{t_{2}}dt{\frac {d}{dt}}\left(\delta x_{i}{\frac {dx_{i}}{dt}}\right).}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d3d0a75604f66354be4b20123019ee46516b215e)














































![{\displaystyle {\begin{aligned}\mathbf {L} &=\sum _{i}\left[\left(\mathbf {R} +\mathbf {r} _{i}\right)\times m_{i}\mathbf {V} _{i}\right]\\&=\sum _{i}\left[\mathbf {R} \times m_{i}\mathbf {V} _{i}+\mathbf {r} _{i}\times m_{i}\mathbf {V} _{i}\right]\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/77077ef30b49ac992b78c6a4c6446709bb1720a9)
![{\displaystyle {\begin{aligned}\mathbf {L} &=\sum _{i}\left[\mathbf {R} \times m_{i}\left(\mathbf {V} +\mathbf {v} _{i}\right)+\mathbf {r} _{i}\times m_{i}(\mathbf {V} +\mathbf {v} _{i})\right]\\&=\sum _{i}\left[\mathbf {R} \times m_{i}\mathbf {V} +\mathbf {R} \times m_{i}\mathbf {v} _{i}+\mathbf {r} _{i}\times m_{i}\mathbf {V} +\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\right]\\&=\sum _{i}\mathbf {R} \times m_{i}\mathbf {V} +\sum _{i}\mathbf {R} \times m_{i}\mathbf {v} _{i}+\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {V} +\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4784bd78e4066783f47bd72472bfa49a0887b0bf)








![{\displaystyle {\begin{aligned}\mathbf {L} &=M(\mathbf {R} \times \mathbf {V} )+\sum _{i}\left[m_{i}\left(\mathbf {r} _{i}\times \mathbf {v} _{i}\right)\right],\\&={\frac {R^{2}}{R^{2}}}M\left(\mathbf {R} \times \mathbf {V} \right)+\sum _{i}\left[{\frac {r_{i}^{2}}{r_{i}^{2}}}m_{i}\left(\mathbf {r} _{i}\times \mathbf {v} _{i}\right)\right],\\&=R^{2}M\left({\frac {\mathbf {R} \times \mathbf {V} }{R^{2}}}\right)+\sum _{i}\left[r_{i}^{2}m_{i}\left({\frac {\mathbf {r} _{i}\times \mathbf {v} _{i}}{r_{i}^{2}}}\right)\right],\\\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d5324c7fa7e5e94893f678fab046c2538416bc51)































![{\displaystyle \left[\hbar ^{2}n(n+1)\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/dd720bdca13e8588818fb477347fb90c9789bb4a)


















