Top Qs
Timeline
Chat
Perspective
Blade–vortex interaction
From Wikipedia, the free encyclopedia
Remove ads
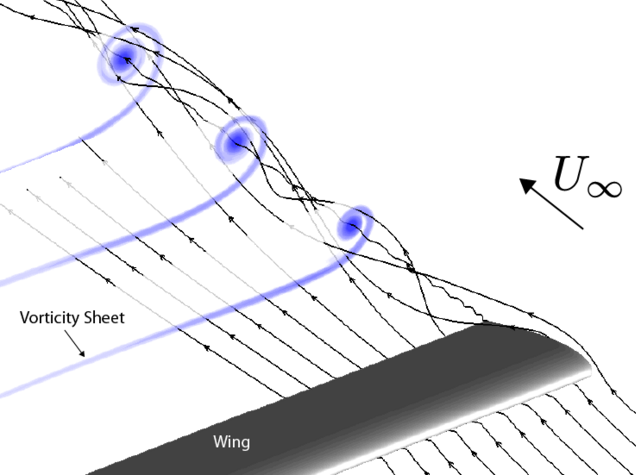
A blade vortex interaction (BVI) is an unsteady phenomenon of three-dimensional nature, which occurs when a rotor blade passes within a close proximity of the shed tip vortices from a previous blade. The aerodynamic interactions represent an important topic of investigation in rotorcraft research field due to the adverse influence produced on rotor noise, particularly in low speed descending flight condition or maneuver, which generates high amplitude impulsive noise.

Remove ads
Classes of blade vortex interactions
Summarize
Perspective
Literature distinguishes different classes of BVIs in helicopter rotors depending on the impacting vortex axis with respect to the blade span.[1][2] Generally, It can be divided into four distinct types, which will be described as follows:
Parallel BVI
Parallel BVI occurs when the vortex and the blade axes are nominally parallel. It is the BVI phenomenon that produces the largest-amplitude impulse (harmonic) noise, due to that the unsteady vortex moves towards to the downstream.[3][4]
Perpendicular BVI
Perpendicular BVI occurs when the axes are perpendicular and in parallel planes. Due to its low unsteadiness, the noise effect of perpendicular BVI are less significant with respect to parallel BVI. It produces a continuous broadband noise characterised by a much lower intensity compared to the impulse (harmonic) noise, which caused by parallel BVI.[5][6]
Oblique BVI
Oblique BVI occurs between the vortex and the blade when the axes are oblique. In helicopter research field, oblique BVI is a common phenomenon that looks like an intermediate action of parallel BVI and perpendicular BVI.
Orthogonal BVI
Orthogonal BVI occurs when the axes of the vortex are in orthogonal planes. In the context of helicopter application, the orthogonal interaction usually exits between the tip vortices generated by the main rotor and the blade of the tail rotor.
Remove ads
Means of BVIs prediction
Summarize
Perspective
As a predominant source of noise, BVI phenomenon can be detrimental to blade structure integrity as well because of the unsteady fluctuation of aerodynamics, such as vortex buffeting and dynamic stall in the retreating blade. Therefore, BVI becomes a prime concern in the helicopter research field. In order to understand the BVI flow characteristic more closely and suppress the noise and vibration actively, it is important to predict the BVIs precisely. Recently, the tools for capturing BVIs can be divided into three parts, which will be described as follows:
Wind tunnel test

As for aerodynamic problems, wind tunnel test is a basic tool used in research. In 1994, researchers from German DLR, French ONERA, NASA Langley, and the US Army Aeroflightdynamics Directorate (AFDD) formed an international consortium to carry out a comprehensive experimental program which is denominated HART I (Higher Harmonic Control Aeroacoustic Rotor Test I) project at the large low speed facility of DNW (German-Dutch wind tunnel). In this test, a 40% scaled BO-105 rotor model along with a fuselage is used, a range of sophisticated measurement techniques are introduced to measure the noise level, blade surface pressure, tip vortices, blade motions, and structural moments with and without the application of HHC (Higher Harmonic Control) pitch control inputs.[7] In 2001, an update program named HART II was conducted to improve the basic understanding and the analytical modeling capabilities of rotor BVI noise with and without higher harmonic pitch control (HHC) inputs, particularly the effect of rotor wakes on rotor noise and vibration.[8]
Analytical methods
The accurate simulation of the vortex structure in the wake is a crucial part on BVI research. Currently,the analytical methods for BVI phenomenon capturing are mainly based on the free wake model, which has highly efficiency but serious dependence on empirical parameters and cannot include air viscosity effect, furthermore, the aerodynamics calculated in free wake model are based on the lifting-line theory with the drawback in air load capturing and flow field describing, especially for the characteristics of transonic flow.[9]
Computational fluid dynamics methods
In the last fifty years, Computational Fluid Dynamics (CFD) methods experienced great development since the CFD method was first applied to the helicopter research in the 1970s.[10] The development of rotor CFD has undergone three stages.
- Full-Potential Equations
- Euler Equations
- Navier–Stokes Equations (RANS, LES)
The full-potential equations are based on the potential flow theory, but the result computed by this method is usually larger than the real one as it ignored the effect of wake. Currently, it can be applied for predicting BVIs as well due to the excellent advantages in computational efficiency.[11] With the development of computer technology, Euler/Navier-Stokes equations started to be used for rotor aerodynamic research. Compared with the full-potential equation, Euler/Navier-Stokes equations can not only accurately capture the nonlinear flow phenomenon of the rotor flow field, but can also capture the motion of the blade tip vortex in the computational domain. At present, Euler/Navier-Stokes equations have become the dominant method in the field of rotor CFD of helicopter. However, due to the complicate the rotor flow field, there are still many problems need to be solved, such as blade motion, elastic deformation, mesh density and rotor wake capture.
Hybrid methods
Currently, researchers have developed some kind of hybrid technologies to tackle the above problems. For example, high fidelity detached eddy simulation (DES) method was conducted to precisely predict air loads near the blade;[12][13] the adapted Chimera grids method was used for accurately capturing the vortex shed by blades;[14] the CFD/CSD (Computational Structure Dynamics) was carried out widely to more effectively account for the change of the flow field caused by the elastic deformation of blades.[15] Meanwhile, some scholars have begun to introduce high-resolution discrete vortex model(DVM) into the CFD/CSD method. The CFD/CSD/DVM method can not only improve the accuracy of calculation of BVIs, but also effectively eliminate the shortcomings of CFD methods on numerical, furthermore, it can greatly decrease the computation sources.[16][17][18] It is an important direction that is worthy of further development in BVI prediction.
Remove ads
See also
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
