Top Qs
Timeline
Chat
Perspective
Clique (graph theory)
Adjacent subset of an undirected graph From Wikipedia, the free encyclopedia
Remove ads
In graph theory, a clique (/ˈkliːk/ or /ˈklɪk/) is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent. That is, a clique of a graph is an induced subgraph of that is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs. Cliques have also been studied in computer science: the task of finding whether there is a clique of a given size in a graph (the clique problem) is NP-complete, but despite this hardness result, many algorithms for finding cliques have been studied.

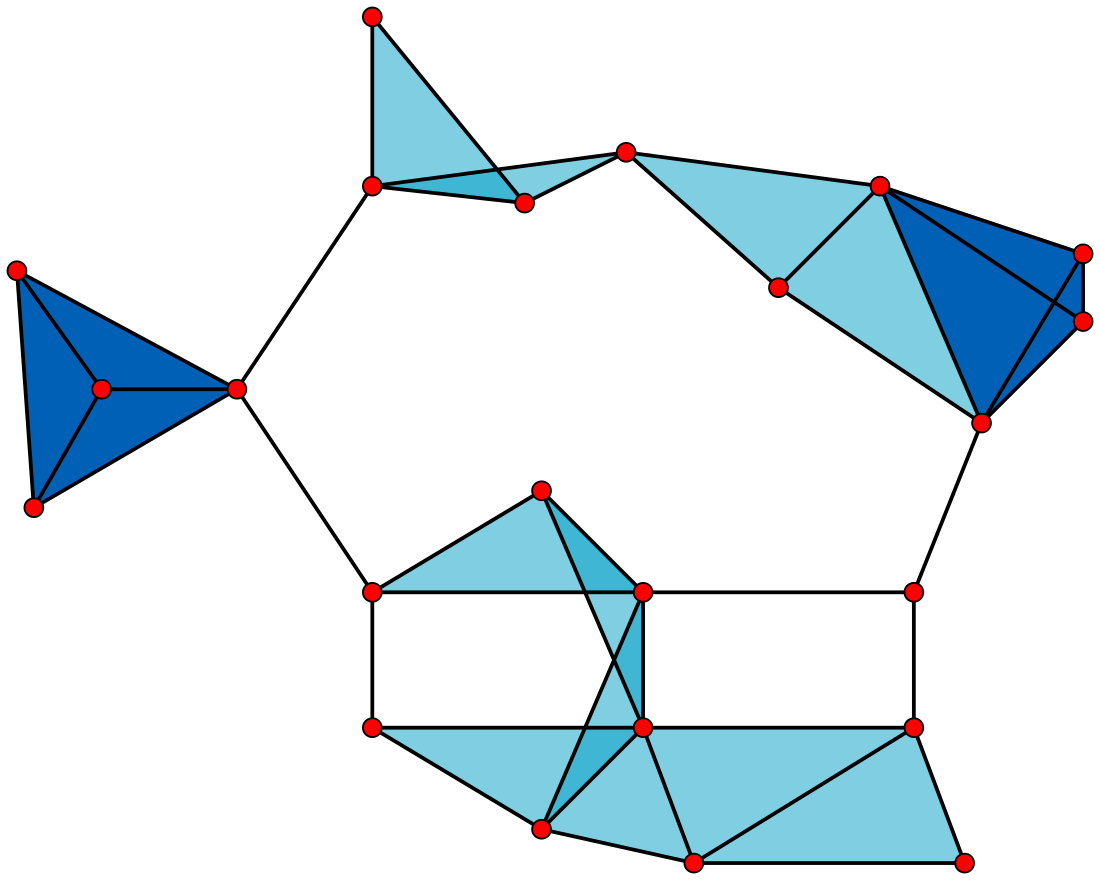
- 23 × 1-vertex cliques (the vertices),
- 42 × 2-vertex cliques (the edges),
- 19 × 3-vertex cliques (light and dark blue triangles), and
- 2 × 4-vertex cliques (dark blue areas).
Although the study of complete subgraphs goes back at least to the graph-theoretic reformulation of Ramsey theory by Erdős & Szekeres (1935),[1] the term clique comes from Luce & Perry (1949), who used complete subgraphs in social networks to model cliques of people; that is, groups of people all of whom know each other. Cliques have many other applications in the sciences and particularly in bioinformatics.
Remove ads
Definitions
Summarize
Perspective
A clique, C, in an undirected graph G = (V, E) is a subset of the vertices, C ⊆ V, such that every two distinct vertices are adjacent. This is equivalent to the condition that the induced subgraph of G induced by C is a complete graph. In some cases, the term clique may also refer to the subgraph directly.
A maximal clique is a clique that is not a subset of any larger clique. Some authors define cliques in a way that requires them to be maximal, and use other terminology for complete subgraphs that are not maximal.
A maximum clique of a graph, G, is a clique, such that there is no clique with more vertices. Moreover, the clique number ω(G) of a graph G is the number of vertices in a maximum clique in G.
The intersection number of G is the smallest number of cliques that together cover all edges of G.
The clique cover number of a graph G is the smallest number of cliques of G whose union covers the set of vertices V of the graph.
A maximum clique transversal of a graph is a subset of vertices with the property that each maximum clique of the graph contains at least one vertex in the subset.[2]
The opposite of a clique is an independent set, in the sense that every clique corresponds to an independent set in the complement graph. The clique cover problem concerns finding as few cliques as possible that include every vertex in the graph.
A related concept is a biclique, a complete bipartite subgraph. The bipartite dimension of a graph is the minimum number of bicliques needed to cover all the edges of the graph.
Remove ads
Mathematics
Summarize
Perspective
Mathematical results concerning cliques include the following.
- Turán's theorem gives a lower bound on the size of a clique in dense graphs.[3] If a graph has sufficiently many edges, it must contain a large clique. For instance, every graph with vertices and more than edges must contain a three-vertex clique.
- Ramsey's theorem states that every graph or its complement graph contains a clique with at least a logarithmic number of vertices.[4]
- According to a result of Moon & Moser (1965), a graph with 3n vertices can have at most 3n maximal cliques. The graphs meeting this bound are the Moon–Moser graphs K3,3,..., a special case of the Turán graphs arising as the extremal cases in Turán's theorem.
- Hadwiger's conjecture, still unproven, relates the size of the largest clique minor in a graph (its Hadwiger number) to its chromatic number.
- The Erdős–Faber–Lovász conjecture relates graph coloring to cliques.
- The Erdős–Hajnal conjecture states that families of graphs defined by forbidden graph characterization have either large cliques or large cocliques.
Several important classes of graphs may be defined or characterized by their cliques:
- A cluster graph is a graph whose connected components are cliques.
- A block graph is a graph whose biconnected components are cliques.
- A chordal graph is a graph whose vertices can be ordered into a perfect elimination ordering, an ordering such that the neighbors of each vertex v that come later than v in the ordering form a clique.
- A cograph is a graph all of whose induced subgraphs have the property that any maximal clique intersects any maximal independent set in a single vertex.
- An interval graph is a graph whose maximal cliques can be ordered in such a way that, for each vertex v, the cliques containing v are consecutive in the ordering.
- A line graph is a graph whose edges can be covered by edge-disjoint cliques in such a way that each vertex belongs to exactly two of the cliques in the cover.
- A perfect graph is a graph in which the clique number equals the chromatic number in every induced subgraph.
- A split graph is a graph in which some clique contains at least one endpoint of every edge.
- A triangle-free graph is a graph that has no cliques other than its vertices and edges.
Additionally, many other mathematical constructions involve cliques in graphs. Among them,
- The clique complex of a graph G is an abstract simplicial complex X(G) with a simplex for every clique in G
- A simplex graph is an undirected graph κ(G) with a vertex for every clique in a graph G and an edge connecting two cliques that differ by a single vertex. It is an example of median graph, and is associated with a median algebra on the cliques of a graph: the median m(A,B,C) of three cliques A, B, and C is the clique whose vertices belong to at least two of the cliques A, B, and C.[5]
- The clique-sum is a method for combining two graphs by merging them along a shared clique.
- Clique-width is a notion of the complexity of a graph in terms of the minimum number of distinct vertex labels needed to build up the graph from disjoint unions, relabeling operations, and operations that connect all pairs of vertices with given labels. The graphs with clique-width one are exactly the disjoint unions of cliques.
- The intersection number of a graph is the minimum number of cliques needed to cover all the graph's edges.
- The clique graph of a graph is the intersection graph of its maximal cliques.
Closely related concepts to complete subgraphs are subdivisions of complete graphs and complete graph minors. In particular, Kuratowski's theorem and Wagner's theorem characterize planar graphs by forbidden complete and complete bipartite subdivisions and minors, respectively.
Remove ads
Computer science
In computer science, the clique problem is the computational problem of finding a maximum clique, or all cliques, in a given graph. It is NP-complete, one of Karp's 21 NP-complete problems.[6] It is also fixed-parameter intractable, and hard to approximate. Nevertheless, many algorithms for computing cliques have been developed, either running in exponential time (such as the Bron–Kerbosch algorithm) or specialized to graph families such as planar graphs or perfect graphs for which the problem can be solved in polynomial time.
Applications
Summarize
Perspective
The word "clique", in its graph-theoretic usage, arose from the work of Luce & Perry (1949), who used complete subgraphs to model cliques (groups of people who all know each other) in social networks. The same definition was used by Festinger (1949) in an article using less technical terms. Both works deal with uncovering cliques in a social network using matrices. For continued efforts to model social cliques graph-theoretically, see e.g. Alba (1973), Peay (1974), and Doreian & Woodard (1994).
Many different problems from bioinformatics have been modeled using cliques. For instance, Ben-Dor, Shamir & Yakhini (1999) model the problem of clustering gene expression data as one of finding the minimum number of changes needed to transform a graph describing the data into a graph formed as the disjoint union of cliques; Tanay, Sharan & Shamir (2002) discuss a similar biclustering problem for expression data in which the clusters are required to be cliques. Sugihara (1984) uses cliques to model ecological niches in food webs. Day & Sankoff (1986) describe the problem of inferring evolutionary trees as one of finding maximum cliques in a graph that has as its vertices characteristics of the species, where two vertices share an edge if there exists a perfect phylogeny combining those two characters. Samudrala & Moult (1998) model protein structure prediction as a problem of finding cliques in a graph whose vertices represent positions of subunits of the protein. And by searching for cliques in a protein–protein interaction network, Spirin & Mirny (2003) found clusters of proteins that interact closely with each other and have few interactions with proteins outside the cluster. Power graph analysis is a method for simplifying complex biological networks by finding cliques and related structures in these networks.
In electrical engineering, Prihar (1956) uses cliques to analyze communications networks, and Paull & Unger (1959) use them to design efficient circuits for computing partially specified Boolean functions. Cliques have also been used in automatic test pattern generation: a large clique in an incompatibility graph of possible faults provides a lower bound on the size of a test set.[7] Cong & Smith (1993) describe an application of cliques in finding a hierarchical partition of an electronic circuit into smaller subunits.
In chemistry, Rhodes et al. (2003) use cliques to describe chemicals in a chemical database that have a high degree of similarity with a target structure. Kuhl, Crippen & Friesen (1983) use cliques to model the positions in which two chemicals will bind to each other.
Remove ads
See also
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads