Top Qs
Timeline
Chat
Perspective
Complete graph
Graph in which every two vertices are adjacent From Wikipedia, the free encyclopedia
Remove ads
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges (one in each direction).[1]
Graph theory itself is typically dated as beginning with Leonhard Euler's 1736 work on the Seven Bridges of Königsberg. However, drawings of complete graphs, with their vertices placed on the points of a regular polygon, had already appeared in the 13th century, in the work of Ramon Llull.[2] Such a drawing is sometimes referred to as a mystic rose.[3]
Remove ads
Properties
Summarize
Perspective
The complete graph on n vertices is denoted by Kn. Some sources claim that the letter K in this notation stands for the German word komplett,[4] but the German name for a complete graph, vollständiger Graph, does not contain the letter K, and other sources state that the notation honors the contributions of Kazimierz Kuratowski to graph theory.[5]
Kn has n(n − 1)/2 edges (a triangular number), and is a regular graph of degree n − 1. All complete graphs are their own maximal cliques. They are maximally connected as the only vertex cut which disconnects the graph is the complete set of vertices. The complement graph of a complete graph is an empty graph.
If the edges of a complete graph are each given an orientation, the resulting directed graph is called a tournament.
Kn can be decomposed into n trees Ti such that Ti has i vertices.[6] Ringel's conjecture asks if the complete graph K2n+1 can be decomposed into copies of any tree with n edges.[7] This is known to be true for sufficiently large n.[8][9]
The number of all distinct paths between a specific pair of vertices in Kn+2 is given[10] by
where e refers to Euler's constant, and
The number of matchings of the complete graphs are given by the telephone numbers
- 1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496, 35696, 140152, 568504, 2390480, 10349536, 46206736, ... (sequence A000085 in the OEIS).
These numbers give the largest possible value of the Hosoya index for an n-vertex graph.[11] The number of perfect matchings of the complete graph Kn (with n even) is given by the double factorial (n − 1)!!.[12]
The crossing numbers up to K27 are known, with K28 requiring either 7233 or 7234 crossings. Further values are collected by the Rectilinear Crossing Number project.[13] Rectilinear Crossing numbers for Kn are
Remove ads
Geometry and topology
Summarize
Perspective

A complete graph with n nodes is the edge graph of an (n − 1)-dimensional simplex. Geometrically K3 forms the edge set of a triangle, K4 a tetrahedron, etc. The Császár polyhedron, a nonconvex polyhedron with the topology of a torus, has the complete graph K7 as its skeleton.[15] Every neighborly polytope in four or more dimensions also has a complete skeleton.
K1 through K4 are all planar graphs. However, every planar drawing of a complete graph with five or more vertices must contain a crossing, and the nonplanar complete graph K5 plays a key role in the characterizations of planar graphs: by Kuratowski's theorem, a graph is planar if and only if it contains neither K5 nor the complete bipartite graph K3,3 as a subdivision, and by Wagner's theorem the same result holds for graph minors in place of subdivisions. As part of the Petersen family, K6 plays a similar role as one of the forbidden minors for linkless embedding.[16] In other words, and as Conway and Gordon[17] proved, every embedding of K6 into three-dimensional space is intrinsically linked, with at least one pair of linked triangles. Conway and Gordon also showed that any three-dimensional embedding of K7 contains a Hamiltonian cycle that is embedded in space as a nontrivial knot.
Remove ads
Examples
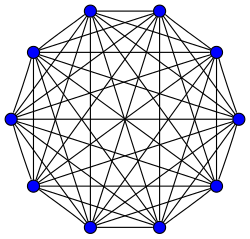
Complete graphs on vertices, for between 1 and 12, are shown below along with the numbers of edges:
See also
- Fully connected network, in computer networking
- Complete bipartite graph (or biclique), a special bipartite graph where every vertex on one side of the bipartition is connected to every vertex on the other side
- The simplex, which is identical to a complete graph of vertices, where is the dimension of the simplex.
Remove ads
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads