Dependency network
From Wikipedia, the free encyclopedia
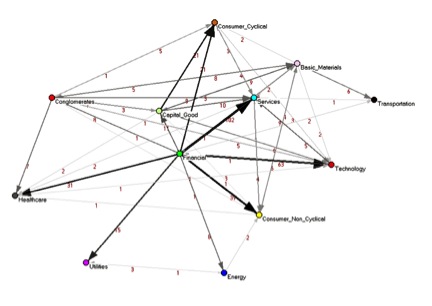
The dependency network approach provides a system level analysis of the activity and topology of directed networks. The approach extracts causal topological relations between the network's nodes (when the network structure is analyzed), and provides an important step towards inference of causal activity relations between the network nodes (when analyzing the network activity). This methodology has originally been introduced for the study of financial data,[1][2] it has been extended and applied to other systems, such as the immune system,[3] and semantic networks.[4]
In the case of network activity, the analysis is based on partial correlations.[5][6][7][8][9] In simple words, the partial (or residual) correlation is a measure of the effect (or contribution) of a given node, say j, on the correlations between another pair of nodes, say i and k. Using this concept, the dependency of one node on another node is calculated for the entire network. This results in a directed weighted adjacency matrix of a fully connected network. Once the adjacency matrix has been constructed, different algorithms can be used to construct the network, such as a threshold network, Minimal Spanning Tree (MST), Planar Maximally Filtered Graph (PMFG), and others.