Top Qs
Timeline
Chat
Perspective
Event (probability theory)
In statistics and probability theory, set of outcomes to which a probability is assigned From Wikipedia, the free encyclopedia
Remove ads
In probability theory, an event is a subset of outcomes of an experiment (a subset of the sample space) to which a probability is assigned.[1] A single outcome may be an element of many different events,[2] and different events in an experiment are usually not equally likely, since they may include very different groups of outcomes.[3] An event consisting of only a single outcome is called an elementary event or an atomic event; that is, it is a singleton set. An event that has more than one possible outcome is called a compound event. An event is said to occur if contains the outcome of the experiment (or trial) (that is, if ).[4] The probability (with respect to some probability measure) that an event occurs is the probability that contains the outcome of an experiment (that is, it is the probability that ). An event defines a complementary event, namely the complementary set (the event not occurring), and together these define a Bernoulli trial: did the event occur or not?
This article needs additional citations for verification. (January 2018) |
Typically, when the sample space is finite, any subset of the sample space is an event (that is, all elements of the power set of the sample space are defined as events).[5] However, this approach does not work well in cases where the sample space is uncountably infinite. So, when defining a probability space it is possible, and often necessary, to exclude certain subsets of the sample space from being events (see § Events in probability spaces, below).
Remove ads
A simple example
Summarize
Perspective
If we assemble a deck of 52 playing cards with no jokers, and draw a single card from the deck, then the sample space is a 52-element set, as each card is a possible outcome. An event, however, is any subset of the sample space, including any singleton set (an elementary event), the empty set (an impossible event, with probability zero) and the sample space itself (a certain event, with probability one). Other events are proper subsets of the sample space that contain multiple elements. So, for example, potential events include:

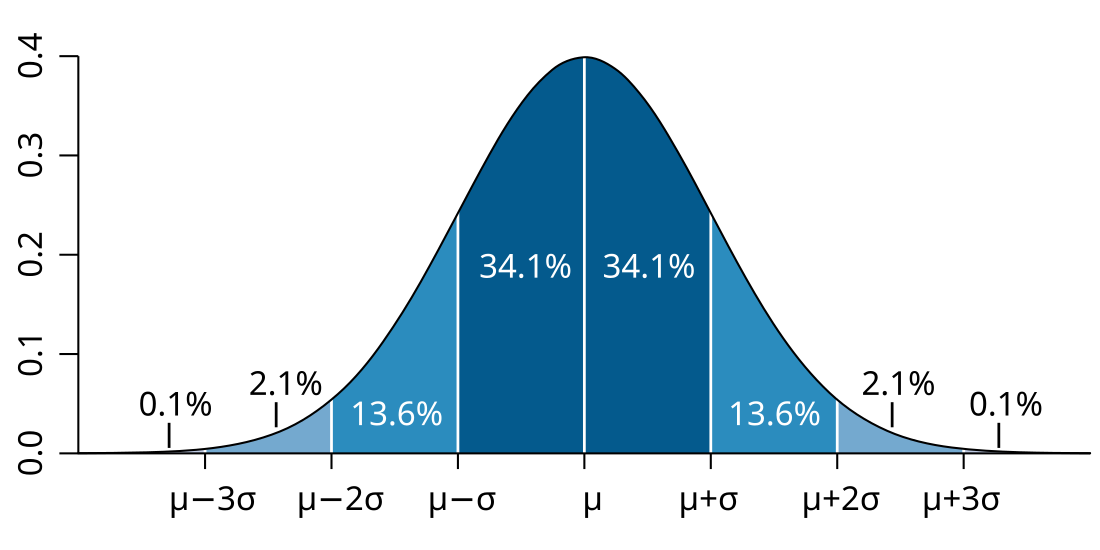
By the ratio of their areas, the probability of is approximately 0.4.
- "Red and black at the same time without being a joker" (0 elements),
- "The 5 of Hearts" (1 element),
- "A King" (4 elements),
- "A Face card" (12 elements),
- "A Spade" (13 elements),
- "A Face card or a red suit" (32 elements),
- "A card" (52 elements).
Since all events are sets, they are usually written as sets (for example, {1, 2, 3}), and represented graphically using Venn diagrams. In the situation where each outcome in the sample space Ω is equally likely, the probability of an event is the following formula: This rule can readily be applied to each of the example events above.
Remove ads
Events in probability spaces
Summarize
Perspective
Defining all subsets of the sample space as events works well when there are only finitely many outcomes, but gives rise to problems when the sample space is infinite. For many standard probability distributions, such as the normal distribution, the sample space is the set of real numbers or some subset of the real numbers. Attempts to define probabilities for all subsets of the real numbers run into difficulties when one considers 'badly behaved' sets, such as those that are nonmeasurable. Hence, it is necessary to restrict attention to a more limited family of subsets. For the standard tools of probability theory, such as joint and conditional probabilities, to work, it is necessary to use a σ-algebra, that is, a family closed under complementation and countable unions of its members. The most natural choice of σ-algebra is the Borel measurable set derived from unions and intersections of intervals. However, the larger class of Lebesgue measurable sets proves more useful in practice.
In the general measure-theoretic description of probability spaces, an event may be defined as an element of a selected 𝜎-algebra of subsets of the sample space. Under this definition, any subset of the sample space that is not an element of the 𝜎-algebra is not an event, and does not have a probability. With a reasonable specification of the probability space, however, all events of interest are elements of the 𝜎-algebra.
Remove ads
A note on notation
Even though events are subsets of some sample space they are often written as predicates or indicators involving random variables. For example, if is a real-valued random variable defined on the sample space the event can be written more conveniently as, simply, This is especially common in formulas for a probability, such as The set is an example of an inverse image under the mapping because if and only if
See also
- Atom (measure theory) – Minimal measurable set with positive measure
- Complementary event – Opposite of a probability event
- Elementary event – Event that contains only one outcome
- Independent event – When the occurrence of one event does not affect the likelihood of another
- Outcome (probability) – Possible result of an experiment or trial
- Pairwise independent events – Set of random variables of which any two are independent
Remove ads
Notes
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads













![{\displaystyle \omega \in X^{-1}((u,v])}](http://wikimedia.org/api/rest_v1/media/math/render/svg/df27f32adf9e5444ae9926d66af8bd2fc6151c58)
