Top Qs
Timeline
Chat
Perspective
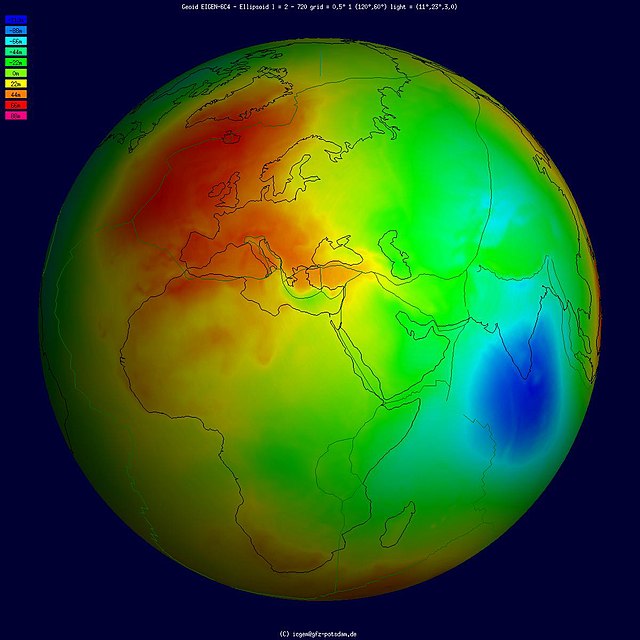
Geoid
Ocean shape without winds and tides From Wikipedia, the free encyclopedia
Remove ads
The geoid (/ˈdʒiː.ɔɪd/ JEE-oyd) is the shape that the ocean surface would take under the influence of the gravity of Earth, including gravitational attraction and Earth's rotation, if other influences such as winds and tides were absent. This surface is extended through the continents (such as might be approximated with very narrow hypothetical canals). According to Carl Friedrich Gauss, who first described it, it is the "mathematical figure of the Earth", a smooth but irregular surface whose shape results from the uneven distribution of mass within and on the surface of Earth.[2] It can be known only through extensive gravitational measurements and calculations. Despite being an important concept for almost 200 years in the history of geodesy and geophysics, it has been defined to high precision only since advances in satellite geodesy in the late 20th century.

The geoid is often expressed as a geoid undulation or geoidal height above a given reference ellipsoid, which is a slightly flattened sphere whose equatorial bulge is caused by the planet's rotation. Generally the geoidal height rises where the Earth's material is locally more dense and exerts greater gravitational force than the surrounding areas. The geoid in turn serves as a reference coordinate surface for various vertical coordinates, such as orthometric heights, geopotential heights, and dynamic heights (see Geodesy).
All points on a geoid surface have the same geopotential (the sum of gravitational potential energy and centrifugal potential energy). At this surface, apart from temporary tidal fluctuations, the force of gravity acts everywhere perpendicular to the geoid, meaning that plumb lines point perpendicular and bubble levels are parallel to the geoid. Being an equigeopotential means the geoid corresponds to the free surface of water at rest (if only the Earth's gravity and rotational acceleration were at work); this is also a sufficient condition for a ball to remain at rest instead of rolling over the geoid. Earth's gravity acceleration (the vertical derivative of geopotential) is thus non-uniform over the geoid.[3]

Remove ads
Description
Summarize
Perspective
The geoid surface is irregular, unlike the reference ellipsoid (which is a mathematical idealized representation of the physical Earth as an ellipsoid), but is considerably smoother than Earth's physical surface. Although the "ground" of the Earth has excursions on the order of +8,800 m (Mount Everest) and −11,000 m (Marianas Trench), the geoid's deviation from an ellipsoid ranges from +85 m (Iceland) to −106 m (southern India), less than 200 m total.[4]
If the ocean were of constant density and undisturbed by tides, currents or weather, its surface would resemble the geoid. The permanent deviation between the geoid and mean sea level is called ocean surface topography. If the continental land masses were crisscrossed by a series of tunnels or canals, the sea level in those canals would also very nearly coincide with the geoid. Geodesists are able to derive the heights of continental points above the geoid by spirit leveling.
Being an equipotential surface, the geoid is, by definition, a surface upon which the force of gravity is perpendicular everywhere, apart from temporary tidal fluctuations. This means that when traveling by ship, one does not notice the undulation of the geoid; neglecting tides, the local vertical (plumb line) is always perpendicular to the geoid and the local horizon tangential to it. Likewise, spirit levels will always be parallel to the geoid.
Simplified example
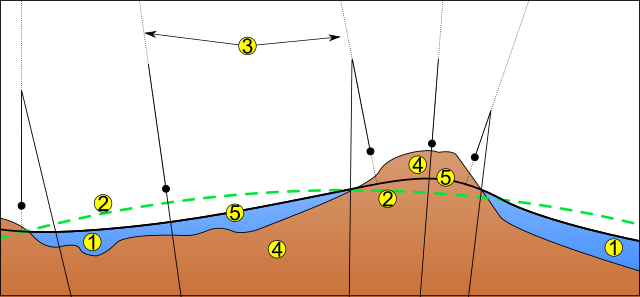
- Ocean
- Ellipsoid
- Local plumb line
- Continent
- Geoid
Earth's gravitational field is not uniform. An oblate spheroid is typically used as the idealized Earth, but even if the Earth were spherical and did not rotate, the strength of gravity would not be the same everywhere because density varies throughout the planet. This is due to magma distributions, the density and weight of different geological compositions in the Earth's crust, mountain ranges, deep sea trenches, crust compaction due to glaciers, and so on.
If that sphere were then covered in water, the water would not be the same height everywhere. Instead, the water level would be higher or lower with respect to Earth's center, depending on the integral of the strength of gravity from the center of the Earth to that location. The geoid level coincides with where the water would be. Generally the geoid rises where the Earth's material is locally more dense, exerts greater gravitational force, and pulls more water from the surrounding area.
Remove ads
Formulation
Summarize
Perspective

The geoid undulation (also known as geoid height or geoid anomaly), N, is the height of the geoid relative to a given ellipsoid of reference. The undulation is not standardized, as different countries use different mean sea levels as reference, but most commonly refers to the EGM96 geoid.
In maps and common use, the height over the mean sea level (such as orthometric height, H) is used to indicate the height of elevations while the ellipsoidal height, h, results from the GPS system and similar GNSS: (An analogous relationship exists between normal heights and the quasigeoid, which disregards local density variations.) In practice, many handheld GPS receivers interpolate N in a pre-computed geoid map (a lookup table).[5]
So a GPS receiver on a ship may, during the course of a long voyage, indicate height variations, even though the ship will always be at sea level (neglecting the effects of tides). That is because GPS satellites, orbiting about the center of gravity of the Earth, can measure heights only relative to a geocentric reference ellipsoid. To obtain one's orthometric height, a raw GPS reading must be corrected. Conversely, height determined by spirit leveling from a tide gauge, as in traditional land surveying, is closer to orthometric height. Modern GPS receivers have a grid implemented in their software by which they obtain, from the current position, the height of the geoid (e.g., the EGM96 geoid) over the World Geodetic System (WGS) ellipsoid. They are then able to correct the height above the WGS ellipsoid to the height above the EGM96 geoid. When height is not zero on a ship, the discrepancy is due to other factors such as ocean tides, atmospheric pressure (meteorological effects), local sea surface topography, and measurement uncertainties.

Remove ads
Determination
Summarize
Perspective
The undulation of the geoid N is closely related to the disturbing potential T according to Bruns' formula (named after Heinrich Bruns):
where is the force of normal gravity, computed from the normal field potential .
Another way of determining N is using values of gravity anomaly , differences between true and normal reference gravity, as per Stokes formula (or Stokes' integral), published in 1849 by George Gabriel Stokes:
The integral kernel S, called Stokes function, was derived by Stokes in closed analytical form.[6] Note that determining anywhere on Earth by this formula requires to be known everywhere on Earth, including oceans, polar areas, and deserts. For terrestrial gravimetric measurements this is a near-impossibility, in spite of close international co-operation within the International Association of Geodesy (IAG), e.g., through the International Gravity Bureau (BGI, Bureau Gravimétrique International).
Another approach for geoid determination is to combine multiple information sources: not just terrestrial gravimetry, but also satellite geodetic data on the figure of the Earth, from analysis of satellite orbital perturbations, and lately from satellite gravity missions such as GOCE and GRACE. In such combination solutions, the low-resolution part of the geoid solution is provided by the satellite data, while a 'tuned' version of the above Stokes equation is used to calculate the high-resolution part, from terrestrial gravimetric data from a neighbourhood of the evaluation point only.
Calculating the undulation is mathematically challenging.[7][8] The precise geoid solution by Petr Vaníček and co-workers improved on the Stokesian approach to geoid computation.[9] Their solution enables millimetre-to-centimetre accuracy in geoid computation, an order-of-magnitude improvement from previous classical solutions.[10][11][12][13]
Geoid undulations display uncertainties which can be estimated by using several methods, e.g., least-squares collocation (LSC), fuzzy logic, artificial neural networks, radial basis functions (RBF), and geostatistical techniques. Geostatistical approach has been defined as the most-improved technique in prediction of geoid undulation.[14]
Remove ads
Relationship to mass density
Summarize
Perspective

Variations in the height of the geoidal surface are related to anomalous density distributions within the Earth. Geoid measures thus help understanding the internal structure of the planet. Synthetic calculations show that the geoidal signature of a thickened crust (for example, in orogenic belts produced by continental collision) is positive, opposite to what should be expected if the thickening affects the entire lithosphere. Mantle convection also changes the shape of the geoid over time.[15]

The surface of the geoid is higher than the reference ellipsoid wherever there is a positive gravity anomaly or negative disturbing potential (mass excess) and lower than the reference ellipsoid wherever there is a negative gravity anomaly or positive disturbing potential (mass deficit).[16]
This relationship can be understood by recalling that gravity potential is defined so that it has negative values and is inversely proportional to distance from the body. So, while a mass excess will strengthen the gravity acceleration, it will decrease the gravity potential. As a consequence, the geoid's defining equipotential surface will be found displaced away from the mass excess. Analogously, a mass deficit will weaken the gravity pull but will increase the geopotential at a given distance, causing the geoid to move towards the mass deficit.
The presence of a localized inclusion in the background medium will rotate the gravity acceleration vectors slightly towards or away from a denser or lighter body, respectively, causing a bump or dimple in the equipotential surface.[17]
The largest absolute deviation can be found in the Indian Ocean Geoid Low, 106 meters below the average sea level.[18] Another large feature is the North Atlantic Geoid High (or North Atlantic Geoid Swell), caused in part by the weight of ice cover over North America and northern Europe in the Late Cenozoic Ice Age.[19]
Remove ads
Temporal change
Recent satellite missions, such as the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE) and GRACE, have enabled the study of time-variable geoid signals. The first products based on GOCE satellite data became available online in June 2010, through the European Space Agency.[20][21] ESA launched the satellite in March 2009 on a mission to map Earth's gravity with unprecedented accuracy and spatial resolution. On 31 March 2011, a new geoid model was unveiled at the Fourth International GOCE User Workshop hosted at the Technical University of Munich, Germany.[22] Studies using the time-variable geoid computed from GRACE data have provided information on global hydrologic cycles,[23] mass balances of ice sheets,[24] and postglacial rebound.[25] From postglacial rebound measurements, time-variable GRACE data can be used to deduce the viscosity of Earth's mantle.[26]
Remove ads
Spherical harmonics representation
Summarize
Perspective
Spherical harmonics are often used to approximate the shape of the geoid. The current best such set of spherical harmonic coefficients is EGM2020 (Earth Gravitational Model 2020), determined in an international collaborative project led by the National Imagery and Mapping Agency (now the National Geospatial-Intelligence Agency, or NGA). The mathematical description of the non-rotating part of the potential function in this model is:[27]
where and are geocentric (spherical) latitude and longitude respectively, are the fully normalized associated Legendre polynomials of degree and order , and and are the numerical coefficients of the model based on measured data. The above equation describes the Earth's gravitational potential , not the geoid itself, at location the co-ordinate being the geocentric radius, i.e., distance from the Earth's centre. The geoid is a particular equipotential surface,[27] and is somewhat involved to compute. The gradient of this potential also provides a model of the gravitational acceleration. The most commonly used EGM96 contains a full set of coefficients to degree and order 360 (i.e., ), describing details in the global geoid as small as 55 km (or 110 km, depending on the definition of resolution). The number of coefficients, and , can be determined by first observing in the equation for that for a specific value of there are two coefficients for every value of except for . There is only one coefficient when since . There are thus coefficients for every value of . Using these facts and the formula, , it follows that the total number of coefficients is given by
using the EGM96 value of .
For many applications, the complete series is unnecessarily complex and is truncated after a few (perhaps several dozen) terms.
Still, even higher resolution models have been developed. Many of the authors of EGM96 have published EGM2008. It incorporates much of the new satellite gravity data (e.g., the Gravity Recovery and Climate Experiment), and supports up to degree and order 2160 (1/6 of a degree, requiring over 4 million coefficients),[28] with additional coefficients extending to degree 2190 and order 2159.[29] EGM2020 is the international follow-up that was originally scheduled for 2020 (still unreleased in 2025), containing the same number of harmonics generated with better data.[30]
Remove ads
See also
References
Further reading
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads









![{\displaystyle V={\frac {GM}{r}}\left(1+{\sum _{n=2}^{n_{\text{max}}}}\left({\frac {a}{r}}\right)^{n}{\sum _{m=0}^{n}}{\overline {P}}_{nm}(\sin \phi )\left[{\overline {C}}_{nm}\cos m\lambda +{\overline {S}}_{nm}\sin m\lambda \right]\right),}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9b89c24db57cda0eefb0ebfbca3f5bd031e193fa)

















