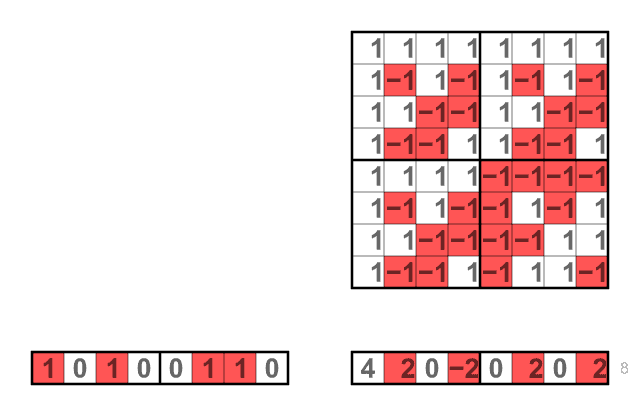
Hadamard transform
Involutive change of basis in linear algebra / From Wikipedia, the free encyclopedia
Dear Wikiwand AI, let's keep it short by simply answering these key questions:
Can you list the top facts and stats about Hadamard gate?
Summarize this article for a 10 year old
The Hadamard transform (also known as the Walsh–Hadamard transform, Hadamard–Rademacher–Walsh transform, Walsh transform, or Walsh–Fourier transform) is an example of a generalized class of Fourier transforms. It performs an orthogonal, symmetric, involutive, linear operation on 2m real numbers (or complex, or hypercomplex numbers, although the Hadamard matrices themselves are purely real).
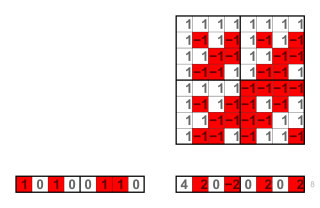
(1, 0, 1, 0, 0, 1, 1, 0) × H(8) = (4, 2, 0, −2, 0, 2, 0, 2)


The Hadamard transform can be regarded as being built out of size-2 discrete Fourier transforms (DFTs), and is in fact equivalent to a multidimensional DFT of size 2 × 2 × ⋯ × 2 × 2.[2] It decomposes an arbitrary input vector into a superposition of Walsh functions.
The transform is named for the French mathematician Jacques Hadamard (French: [adamaʁ]), the German-American mathematician Hans Rademacher, and the American mathematician Joseph L. Walsh.