Loading AI tools
Spiral asymptotic to a line From Wikipedia, the free encyclopedia
A hyperbolic spiral is a type of spiral with a pitch angle that increases with distance from its center, unlike the constant angles of logarithmic spirals or decreasing angles of Archimedean spirals. As this curve widens, it approaches an asymptotic line. It can be found in the view up a spiral staircase and the starting arrangement of certain footraces, and is used to model spiral galaxies and architectural volutes.

As a plane curve, a hyperbolic spiral can be described in polar coordinates by the equation for an arbitrary choice of the scale factor
Because of the reciprocal relation between and it is also called a reciprocal spiral.[1] The same relation between Cartesian coordinates would describe a hyperbola, and the hyperbolic spiral was first discovered by applying the equation of a hyperbola to polar coordinates.[2] Hyperbolic spirals can also be generated as the inverse curves of Archimedean spirals,[3][4] or as the central projections of helixes.[5]
Hyperbolic spirals are patterns in the Euclidean plane, and should not be confused with other kinds of spirals drawn in the hyperbolic plane. In cases where the name of these spirals might be ambiguous, their alternative name, reciprocal spirals, can be used instead.[6]
Pierre Varignon first studied the hyperbolic spiral in 1704,[7][8] as an example of the polar curve obtained from another curve (in this case the hyperbola) by reinterpreting the Cartesian coordinates of points on the given curve as polar coordinates of points on the polar curve. Varignon and later James Clerk Maxwell were interested in the roulettes obtained by tracing a point on this curve as it rolls along another curve; for instance, when a hyperbolic spiral rolls along a straight line, its center traces out a tractrix.[2]
Johann Bernoulli[9] and Roger Cotes also wrote about this curve, in connection with Isaac Newton's discovery that bodies that follow conic section trajectories must be subject to an inverse-square law, such as the one in Newton's law of universal gravitation. Newton asserted that the reverse was true: that conic sections were the only trajectories possible under an inverse-square law. Bernoulli criticized this step, observing that in the case of an inverse-cube law, multiple trajectories were possible, including both a logarithmic spiral (whose connection to the inverse-cube law was already observed by Newton) and a hyperbolic spiral. Cotes found a family of spirals, the Cotes's spirals, including the logarithmic and hyperbolic spirals, that all required an inverse-cube law. By 1720, Newton had resolved the controversy by proving that inverse-square laws always produce conic-section trajectories.[10][11][12][13]
For a hyperbolic spiral with equation , a circular arc centered at the origin, continuing clockwise for length from any of its points, will end on the -axis.[3] Because of this equal-length property, the starting marks of 200m and 400m footraces are placed in staggered positions along a hyperbolic spiral. This ensures that the runners, restricted to their concentric lanes, all have equal-length paths to the finish line. For longer races where runners move to the inside lane after the start, a different spiral (the involute of a circle) is used instead.[14]
The increasing pitch angle of the hyperbolic spiral, as a function of distance from its center, has led to the use of these spirals to model the shapes of some spiral galaxies, which in some cases have a similarly increasing pitch angle. However, this model does not provide a good fit to the shapes of all spiral galaxies.[16][17] In architecture, it has been suggested that hyperbolic spirals are a good match for the design of volutes from columns of the Corinthian order.[18] It also describes the perspective view up the axis of a spiral staircase or other helical structure.[5]
Along with the Archimedean and logarithmic spiral, the hyperbolic spiral has been used in psychological experiments on the perception of rotation.[19]
The hyperbolic spiral has the equation for polar coordinates and scale coefficient . It can be represented in Cartesian coordinates by applying the standard polar-to-Cartesian conversions and , obtaining a parametric equation for the Cartesian coordinates of this curve that treats as a parameter rather than as a coordinate:[20] Relaxing the constraint that to and using the same equations produces a reflected copy of the spiral, and some sources treat these two copies as branches of a single curve.[4][21]
The hyperbolic spiral is a transcendental curve, meaning that it cannot be defined from a polynomial equation of its Cartesian coordinates.[20] However, one can obtain a trigonometric equation in these coordinates by starting with its polar defining equation in the form and replacing its variables according to the Cartesian-to-polar conversions and , giving:[22]
It is also possible to use the polar equation to define a spiral curve in the hyperbolic plane, but this is different in some important respects from the usual form of the hyperbolic spiral in the Euclidean plane. In particular, the corresponding curve in the hyperbolic plane does not have an asymptotic line.[6]

Circle inversion through the unit circle is a transformation of the plane that, in polar coordinates, maps the point (excluding the origin) to and vice versa.[23] The image of an Archimedean spiral under this transformation (its inverse curve) is the hyperbolic spiral with equation .[8]
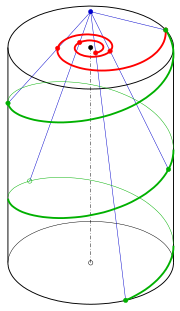
The central projection of a helix onto a plane perpendicular to the axis of the helix describes the view that one would see of the guardrail of a spiral staircase, looking up or down from a viewpoint on the axis of the staircase.[5] To model this projection mathematically, consider the central projection from point onto the image plane . This will map a point to the point .[24]
The image under this projection of the helix with parametric representation is the curve with the polar equation which describes a hyperbolic spiral.[24]
The hyperbolic spiral approaches the origin as an asymptotic point.[22] Because the curve has an asymptotic line with equation .[20]

From vector calculus in polar coordinates one gets the formula for the pitch angle between the tangent of any curve and the tangent of its corresponding polar circle.[25] For the hyperbolic spiral the pitch angle is[19]
The curvature of any curve with polar equation is[26] From the equation and its derivatives and one gets the curvature of a hyperbolic spiral, in terms of the radius or of the angle of any of its points:[27]
The length of the arc of a hyperbolic spiral between the points and can be calculated by the integral:[20] Here, the bracket notation means to calculate the formula within the brackets for both and , and to subtract the result for from the result for .
The area of a sector (see diagram above) of a hyperbolic spiral with equation is:[20] That is, the area is proportional to the difference in radii, with constant of proportionality .[13][20]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.