Top Qs
Timeline
Chat
Perspective
Nerve (category theory)
Simplicial set constructed from the objects and morphisms of a small category From Wikipedia, the free encyclopedia
Remove ads
In category theory, a discipline within mathematics, the nerve N(C) of a small category C is a simplicial set constructed from the objects and morphisms of C. The geometric realization of this simplicial set is a topological space, called the classifying space of the category C. These closely related objects can provide information about some familiar and useful categories using algebraic topology, most often homotopy theory.
Remove ads
Motivation
The nerve of a category is often used to construct topological versions of moduli spaces. If X is an object of C, its moduli space should somehow encode all objects isomorphic to X and keep track of the various isomorphisms between all of these objects in that category. This can become rather complicated, especially if the objects have many non-identity automorphisms. The nerve provides a combinatorial way of organizing this data. Since simplicial sets have a good homotopy theory, one can ask questions about the meaning of the various homotopy groups πn(N(C)). One hopes that the answers to such questions provide interesting information about the original category C, or about related categories.
The notion of nerve is a direct generalization of the classical notion of classifying space of a discrete group; see below for details.
Remove ads
Construction
Summarize
Perspective
Let C be a small category. There is a 0-simplex of N(C) for each object of C. There is a 1-simplex for each morphism f : x → y in C. Now suppose that f: x → y and g : y → z are morphisms in C. Then we also have their composition gf : x → z.

The diagram suggests our course of action: add a 2-simplex for this commutative triangle. Every 2-simplex of N(C) comes from a pair of composable morphisms in this way. The addition of these 2-simplices does not erase or otherwise disregard morphisms obtained by composition, it merely remembers that this is how they arise.
In general, N(C)k consists of the k-tuples of composable morphisms
of C. To complete the definition of N(C) as a simplicial set, we must also specify the face and degeneracy maps. These are also provided to us by the structure of C as a category. The face maps
are given by composition of morphisms at the ith object (or removing the ith object from the sequence, when i is 0 or k).[1] This means that di sends the k-tuple
to the (k − 1)-tuple
That is, the map di composes the morphisms Ai−1 → Ai and Ai → Ai+1 into the morphism Ai−1 → Ai+1, yielding a (k − 1)-tuple for every k-tuple.
Similarly, the degeneracy maps
are given by inserting an identity morphism at the object Ai.
Simplicial sets may also be regarded as functors Δop → Set, where Δ is the category of totally ordered finite sets and order-preserving morphisms. Every partially ordered set P yields a (small) category i(P) with objects the elements of P and with a unique morphism from p to q whenever p ≤ q in P. We thus obtain a functor i from the category Δ to the category of small categories. We can now describe the nerve of the category C as the functor Δop → Set
This description of the nerve makes functoriality transparent; for example, a functor between small categories C and D induces a map of simplicial sets N(C) → N(D). Moreover, a natural transformation between two such functors induces a homotopy between the induced maps. This observation can be regarded as the beginning of one of the principles of higher category theory. It follows that adjoint functors induce homotopy equivalences. In particular, if C has an initial or final object, its nerve is contractible.
Remove ads
Examples
Summarize
Perspective
The primordial example is the classifying space of a discrete group G. We regard G as a category with one object whose endomorphisms are the elements of G. Then the k-simplices of N(G) are just k-tuples of elements of G. The face maps act by multiplication, and the degeneracy maps act by insertion of the identity element. If G is the group with two elements, then there is exactly one nondegenerate k-simplex for each nonnegative integer k, corresponding to the unique k-tuple of elements of G containing no identities. After passing to the geometric realization, this k-tuple can be identified with the unique k-cell in the usual CW structure on infinite-dimensional real projective space. The latter is the most popular model for the classifying space of the group with two elements. See (Segal 1968) for further details and the relationship of the above to Milnor's join construction of BG.
Most spaces are classifying spaces
Every "reasonable" topological space is homeomorphic to the classifying space of a small category. Here, "reasonable" means that the space in question is the geometric realization of a simplicial set. This is obviously a necessary condition; it is also sufficient. Indeed, let X be the geometric realization of a simplicial set K. The set of simplices in K is partially ordered, by the relation x ≤ y if and only if x is a face of y. We may consider this partially ordered set as a category with the relations as morphisms. The nerve of this category is the barycentric subdivision of K, and thus its realization is homeomorphic to X, because X is the realization of K by hypothesis and barycentric subdivision does not change the homeomorphism type of the realization.
The nerve of an open covering
If X is a topological space with open cover Ui, the nerve of the cover is obtained from the above definitions by replacing the cover with the category obtained by regarding the cover as a partially ordered set with set inclusions as relations (and hence morphisms). Note that the realization of this nerve is not generally homeomorphic to X (or even homotopy equivalent): homotopy equivalence will usually hold only for a good cover by contractible sets having contractible intersections.
A moduli example
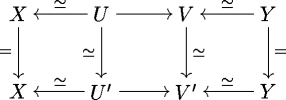
One can use the nerve construction to recover mapping spaces, and even get "higher-homotopical" information about maps. Let D be a category, and let X and Y be objects of D. One is often interested in computing the set of morphisms X → Y. We can use a nerve construction to recover this set. Let C = C(X,Y) be the category whose objects are diagrams
such that the morphisms U → X and Y → V are isomorphisms in D. Morphisms in C(X, Y) are diagrams of the following shape:
Here, the indicated maps are to be isomorphisms or identities. The nerve of C(X, Y) is the moduli space of maps X → Y. In the appropriate model category setting, this moduli space is weak homotopy equivalent to the simplicial set of morphisms of D from X to Y.
Remove ads
Nerve theorem
This section needs expansion with: Actually define the Segal condition. You can help by adding to it. (July 2024) |
The next theorem is due to Grothendieck.
Theorem—A simplicial set is the nerve of a category if and only if it satisfies the Segal conditions.[2]
See also: Segal space, Homotopy category of an ∞-category
Homotopy coherent nerve
This section needs expansion. You can help by adding to it. (March 2025) |
Like a nerve functor, but more generally, the homotopy coherent nerve functor associates to a simplicially enriched category a simpllicial set; i.e.,[3]
For example, the Duskin nerve of a strict 2-category is a special case of this.
See also https://ncatlab.org/nlab/show/homotopy+coherent+nerve for more details.
Remove ads
References
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads