Poncelet–Steiner theorem

In Euclidean geometry, the Poncelet–Steiner theorem is a result about compass and straightedge constructions with certain restrictions. This result states that whatever can be constructed by straightedge and compass together can be constructed by straightedge alone, provided that a single circle and its centre are given.

Construction of a parallel (h) to a diameter g through any given point P, using only a straightedge

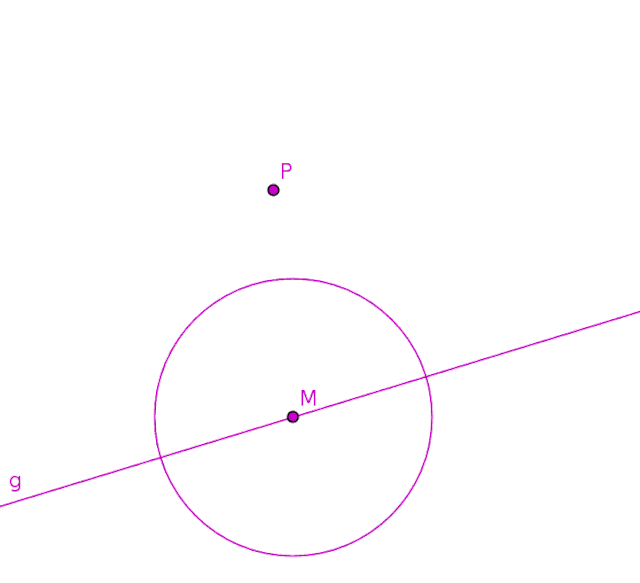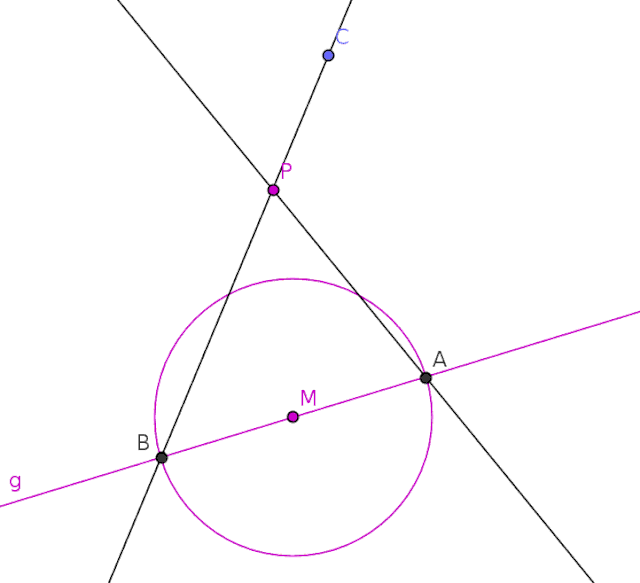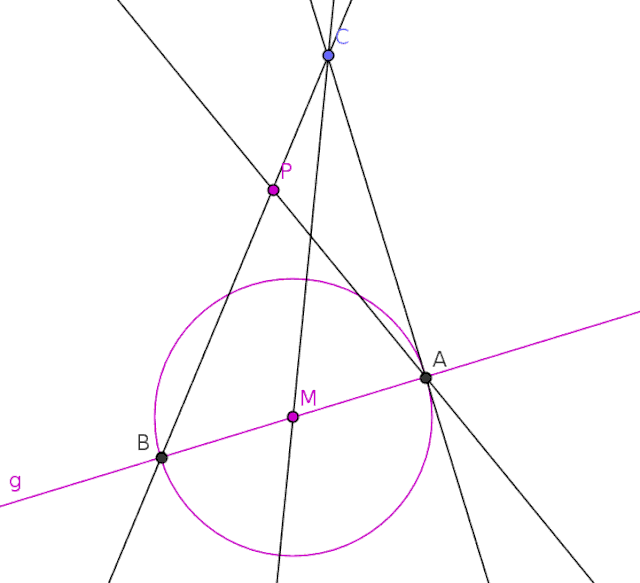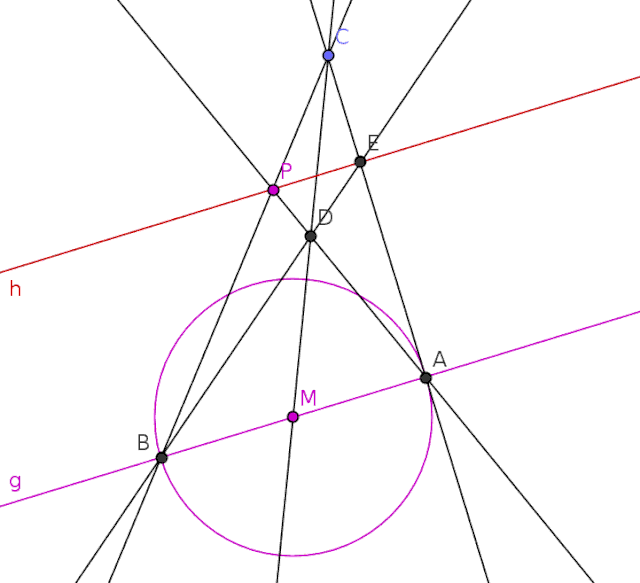
This shows that, while a compass can make constructions easier, it is no longer needed once the first circle has been drawn. All constructions thereafter can be performed using only the straightedge, although the arcs of circles themselves cannot be drawn without the compass. This means the compass may be used for aesthetic purposes, but it is not required for the construction itself.

History

"The geometrical constructions, carried out using the straight line and a fixed circle, as a subject of teaching at higher educational institutions and for practical use; by Jacob Steiner, Doctor of philosophy, Royal Prussian professor and distinguished teacher of mathematics at the commercial school in Berlin. With two copper plaques. Berlin, with Ferdinand Dummler. 1833."

In the tenth century, the Persian mathematician Abu al-Wafa' Buzjani (940−998) considered geometric constructions using a straightedge and a compass with a fixed opening, a so-called rusty compass. Constructions of this type appeared to have some practical significance as they were used by artists Leonardo da Vinci and Albrecht Dürer in Europe in the late fifteenth century. A new viewpoint developed in the mid sixteenth century when the size of the opening was considered fixed but arbitrary and the question of how many of Euclid's constructions could be obtained was paramount.^[1]

Renaissance mathematician Lodovico Ferrari, a student of Gerolamo Cardano in a "mathematical challenge" against Niccolò Fontana Tartaglia was able to show that "all of Euclid" (that is, the straightedge and compass constructions in the first six books of Euclid's Elements) could be accomplished with a straightedge and rusty compass. Within ten years additional sets of solutions were obtained by Cardano, Tartaglia and Tartaglia's student Benedetti.^[2] During the next century these solutions were generally forgotten until, in 1673, Georg Mohr published (anonymously and in Dutch) Euclidis Curiosi containing his own solutions. Mohr had only heard about the existence of the earlier results and this led him to work on the problem.^[3]

Showing that "all of Euclid" could be performed with straightedge and rusty compass is not the same as proving that all straightedge and compass constructions could be done with a straightedge and just a rusty compass. Such a proof would require the formalization of what a straightedge and compass could construct. This groundwork was provided by Jean Victor Poncelet in 1822, having been motivated by Mohr's work on the Mohr–Mascheroni theorem. He also conjectured and suggested a possible proof that a straightedge and rusty compass would be equivalent to a straightedge and compass, and moreover, the rusty compass need only be used once. The result of this theorem, that a straightedge and single circle with given centre is equivalent to a straightedge and compass was proved by Jakob Steiner in 1833.^[4][1]

Related constructs

Constructs related to the Poncelet–Steiner theorem.

Steiner constructions

Named after Jakob Steiner, the term Steiner construction refers to any geometric construction that only utilizes the straightedge, and is sometimes called a straightedge-only construction.^[5] The Poncelet–Steiner theorem covers a particular subset of Steiner constructions: those in which a fixed circle and its center are present on the plane. In this sense, all constructions adhering to the Poncelet–Steiner theorem are Steiner constructions, though not all Steiner constructions abide by the same restrictions.

Rusty compass

The rusty compass describes a compass whose distance is fixed — its hinge is so rusted that its legs are unable to adjust width. Circles may be drawn centered at any arbitrary point, but the radius is unchangeable. Historically, it was shown that all Euclid constructions can be performed with a rusty compass and straightedge. The Poncelet–Steiner theorem generalizes this further, showing that a single arbitrarily placed circle with its center is sufficient to replace all further use of the compass.

Constructive proof

Outline

To prove the Poncelet–Steiner theorem, it suffices to show that each of the basic constructions of compass and straightedge is possible using a straightedge alone (provided that a circle and its center exist in the plane), as these are the foundations of all other constructions. All constructions can be written as a series of steps involving these five basic constructions:

The basic constructions 1 through 5 illustrated, from left to right. The top row being the information given, the bottom row being the desired construction; red indicating the newer information.

1. Creating the line through two existing points.
2. Creating the circle through one point with centre another point.
3. Creating the point which is the intersection of two existing, non-parallel lines.
4. Creating the one or two points in the intersection of a line and a circle (if they intersect).
5. Creating the one or two points in the intersection of two circles (if they intersect).

Constructions (1) and (3) can be done with a straightedge alone. For construction (2), a circle is considered to be given by any two points, one defining the center and one existing on the circumference at radius. It is understood that the arc of a circle cannot be drawn without a compass, so in keeping with the intent of the theorem, the actual circle need not be drawn.

Thus, the proof of the theorem lies in showing that constructions (4) and (5) are possible using only a straightedge, along with a fixed circle and its center. Once this is done, it follows that every compass-straightedge construction can be done under the restrictions of the theorem.

The following proof is based on the one given by Howard Eves in 1963.^[1]

Notation

In the constructions below, a circle defined by a center point P and a point on its circumference, Q, through which the arc of the circle passes (or would pass if compass-drawn), is denoted as P(Q). The given circle is denoted as O(r) with center O, and is the only compass-drawn circle on the plane.

Some preliminary constructions

To prove the above constructions (4) and (5), a few necessary intermediary constructions are also explained below since they are used and referenced frequently. These are also straightedge-only constructions.

Constructing a parallel of a line having a bisected segment

This construction does not require the use of the given circle. Naturally any line that passes through the center of the given circle implicitly has a bisected segment: the diameter is bisected by the center. The animated GIF file embedded at the introduction to this article demonstrates this construction, which is reiterated here without the circle and with enumerated steps.

Construction of a parallel line through an arbitrary point, of a given arbitrary line having a bisected segment embedded.

Given an arbitrary line n (in black) with two marked points A and B, and their midpoint M, and an arbitrary point P in the plane (assumed not to be on line n), we wish to construct the parallel of line n through P:

1. Construct a line AP (in red).
2. Construct a line BP (in orange).
3. Choose an arbitrary point R on line AP.
4. Construct a line BR (in green).
5. Construct a line MR (in light blue).
6. Lines MR and BP intersect at point X.
7. Construct a line AX (in magenta).
8. Lines BR and AX intersect at point Q.
9. Construct a line PQ (in dark blue), the desired parallel.

This construction is a special case of the projective harmonic conjugate construction.

Constructing a bisected segment on a line

If the line passes through the center of a circle, the segment defined by the diameter through the circle is bisected by the center. In the general case, however, any other line in the plane may have a bisected segment constructed onto it. This construction makes use of the given circle, O(r).

Construction of an arbitrary bisected line segment on a given line.

Given a line, m (in black), we wish to construct points A, B, and C on the line such that B is the midpoint:

1. Draw an arbitrary line (in red) passing through the given circle's center, O, and the desired midpoint B (chosen arbitrarily) on the line m.
   • Notice that the red line, OB, passes through the center of the circle and highlights a diameter, bisected by the circle center. Any parallel may be made from this line according to the previous construction.
2. Choose an arbitrary point D on the given circle
   • The point D should be chosen such that line OD and line OB are not perpendicular.
3. Construct a line (in orange), passing through D, that is parallel to the red line OB.
   • This parallel intersects the given circle at E.
   • This parallel also intersects the black line m at A, defining one end of the line segment.
4. Create two lines (in green), OD and OE, that each pass through the given circle's center.
   • These green lines intersect the given circle at points F and G, respectively.
5. Line FG (in blue) intersects the line m at C, defining the other endpoint of the line segment.
   • Segment EH now exists coincident with line m and having midpoint B.

Constructing a parallel of any line

This construction generalizes the parallel line construction to all possible lines, not just the ones with a collinear bisected line segment.

To construct a parallel line of any given line, through any point in the plane, we combine the two previous constructions:

1. Any line from which a parallel is to be made must have a bisected segment constructed onto it, if one does not already exist.
2. A parallel is then constructed according to the previous parallel construction involving the collinear bisected segment.

Constructing a perpendicular line

Construction of a perpendicular line.

This construction makes use of the given circle O(r) by taking advantage of Thales's theorem.

Given a line m and a point A in the plane, we wish to construct a perpendicular to line m through A:

1. If line m does not pass through the given circle (as depicted), or it passes through the given circle's center, then a new parallel line (in red) is constructed arbitrarily such that it does pass through the given circle but not its center, and the perpendicular is to be made from this line instead.
2. This red line which passes through the given circle but not its center, will intersect the given circle in two points, B and C.
3. Draw a line BO (in orange), through the circle center.
   • This line intersects the given circle at point D.
4. Draw a line DC (in light green).
   • By Thales's theorem, ∠BCD is a right angle, so this line is perpendicular to the red (and therefore the black) lines, BC and m.
5. Construct a parallel of line DC through point A using previous constructions.
   • This line is perpendicular to line m and passes through point A.

Another option in the event the line passes through the circle's center would be to construct a parallel to it through the circle at an arbitrary point. An isosceles trapezoid (or potentially an isosceles triangle) is formed by the intersection points to the circle of both lines. The two non-parallel sides of which may be extended to an intersection point between them, and a line drawn from there through the circle's center. This line is perpendicular, and the diameter is bisected by the center.

Constructing the midpoint of any segment (segment bisection)

Construction of the midpoint of an arbitrary line segment from a non-collinear parallel line.

Given a line segment AB, we wish to construct its midpoint M:

1. Construct a line m parallel to line segment AB using previous constructions.
   • The parallel may be placed in the plane arbitrarily, as long as it does not coincide with the line segment.
2. Choose an arbitrary point C in the plane which is not collinear with the line or the line segment.
3. Draw a line AC (in red), intersecting line m at point D.
4. Draw a line BC (in orange), intersecting line m at point E.
5. Draw two lines, AE and BD (each in light green), intersecting each other at point X
6. Draw a line CX (in blue), intersecting segment AB at point M.
   • Point M is the desired midpoint of segment AB.

This construction is the same as the previous construction of a parallel from a bisected line segment, but with the steps done in reverse.

Constructing the radical axis between circles

Straightedge-only construction of the radical axis between circles.

Suppose two circles A(B) and C(D) are implicitly given, defined only by the points A, B, C, and D in the plane, with their centers defined, but are not compass-drawn. The radical axis, line m (in dark blue), between the two circles may be constructed:

1. Draw a line AC (in orange) through the circle centers.
2. Draw a line segment BD (in red) between the points on the circumference of the circles.
3. Find the midpoint, M, of segment BD.
4. Draw lines AM and CM (both in light green), connecting the segment midpoint with each of the circle centers.
5. Construct a line j (in purple) passing through point B, and perpendicular to AM.
   • Line j is the radical axis between circle M(B) and circle A(B), as it passes through the point of intersection B and is perpendicular to the line through centers, AM.
6. Construct a line k (in dark green) passing through point D, and perpendicular to CM.
   • Line k is the radical axis between circle M(B) = M(C) and circle C(D).
7. Lines j and k intersect at point X.
   • Point X is the power center between circles A(B), C(D), and M(B), and is therefore the unique point that lies on the radical axis between any two of the three circles.
   • By transitivity, therefore, point X exists on the radical axis between circles A(B) and C(D).
   • If the lines j and k are parallel then the segment midpoint M is on the line AC — the centers of circles A(B), C(D), and M(B) are collinear — and the construction will fail. An alternative approach is required (see below).
8. Construct a line m (in dark blue) perpendicular to line AC and passing through point X.
   • Line m is the desired radical axis.

In the event that the construction of the radical axis fails due to there not being an intersection point X between parallel lines j and k, which results from the coincidental placement of the midpoint M on the line AC, an alternative approach might be required. One such approach is to choose a different point M' on the perpendicular bisector of segment BD (constructed by drawing the perpendicular through M), then continuing the construction using point M' instead of M.

Intersecting a line with a circle

The straightedge-only construction of the intersection points between a line and a circle.

The fourth basic construction concerns the intersection of a line with a circle. The construction below makes use of the given circle, O(r), by taking advantage of homothety.

In the diagram, there is a homothety sending circle P(Q) to the given circle O(r). By mapping line m under the same homothety, the problem of finding the intersections to P(Q) can be reduced to finding the intersections to O(r).

Given a line m (in black) and a circle P(Q), which is not compass-drawn, we wish to create their intersection points A and B:

1. Draw a line PQ (in red) through the points defining the circle.
   • If point O is collinear with line PQ, an alternative approach might be required (see below).
2. Construct a parallel (in orange) of line PQ through the center O of the provided circle.
   • The parallel intersects the provided circle at two points, one of which is arbitrarily chosen: R.
3. Draw a line PO (in light green), through the centers of the two circles.
4. Draw a line QR (in light blue), connecting the two points on the circumferences of the two circles.
5. Intersect the lines PO and QR at point X.
   • Point X is the center of homothety sending circle P(Q) to the circle O(r).
   • If point X does not exist due to lines PO and QR being parallel — which results from circles P(Q) and O(r) having equal radii — an alternative approach might be required (see below).
6. Choosing a point M arbitrarily on line m, such that it is not on line PO, draw a line PM (in magenta).
   • If point M does not exist due to lines PO and m coinciding, an alternative approach might be required (see below).
7. Draw a line MX (in brown).
8. Construct a parallel (in dark purple) of line PM through the center O of the given circle.
   • The parallel intersects the line MX at a point N.
9. Construct a parallel (in yellow) of line m through the point N.
   • The parallel intersects the provided circle at points C and D.
   • If the parallel does not intersect the provided circle then neither does the line m intersect circle P(Q).
10. Draw lines CX and DX (both in dark blue).
    • These lines both intersect line m at points A and B, respectively.
11. Points A and B are the desired points of intersection between the line m and the circle P(Q).

In the event that the construction fails due to coincidental placement of points or lines, an alternative approach might be required. One such approach is to choose an arbitrary point on the plane, and performing an intermediate homothety about that point to avoid issues with the construction:

1. Construct an arbitrary point T.
2. Construct the midpoints P' and Q' of PT
3. Construct the midline m' between line m and point T.
   • This can be done by choosing any two points U, V on line m, constructing midpoints U' and V' of UT and VT, then drawing line U'V' .
4. Use the construction above to get the intersection points A' and B' between the line m' and the circle P'(Q').
5. Draw lines A'T and B'T.
   • These lines intersect line m at points A and B respectively.
6. Points A and B are the desired points of intersection between the line m and the circle P(Q).

Intersecting two circles

The fifth basic construction concerns the intersection of two circles, which can be constructed by combining two earlier constructions.

Suppose two circles A(B) and C(D) are implicitly given, defined only by the points A, B, C, and D in the plane, with their centers defined, but are not compass-drawn. Their intersection points, U and V, may be constructed:

1. Construct the radical axis, line m, between the two circles.
2. Construct the intersection points, U and V, between the radical axis, line m, and either one of the two circles arbitrarily chosen.
   • The radical axis is a line, so this construction is possible per the previous circle-line intersection construction.
3. These points are the desired points of intersection of the circles.
   • The two circles and the radical axis all intersect at the same loci of points: two distinct points, one point if they are tangent, or none if they do not intersect.
   • If the radical axis does not intersect one circle then it intersects neither, and neither do the two circles intersect.

Conclusion

Since all five basic constructions have been shown to be achievable with only a straightedge, provided that a single circle with its center is placed in the plane, this proves the Poncelet–Steiner theorem. Any compass-straightedge construction may be achieved with the straightedge alone by describing their constructive steps in terms of the five basic constructions.

Alternative proofs

Alternative proofs do exist for the Poncelet–Steiner theorem, originating in an algebraic approach to geometry. Relying on equations and numerical values in real coordinate space, ${\displaystyle \mathbb {R} ^{2}}$, via an isomorphism to the Euclidean plane, this is a fairly modern interpretation which requires the notions of length, distance, and coordinate positions to be imported into the plane.

Other types of restricted construction

Compass-Only Constructions

Main article: Mohr–Mascheroni theorem

The Poncelet–Steiner theorem can be contrasted with the Mohr–Mascheroni theorem, which states that any compass and straightedge construction can be performed with only a compass. The straightedge is not required, except for aesthetic purposes. Constructions carried out using only the compass are often called Mascheroni constructions, or simply compass-only constructions.

Rusty Compass

The rusty compass restriction allows the use of a compass and straightedge, provided that the compass produces circles of fixed radius. Although the rusty compass constructions were explored since the 10th century, and all of Euclid was shown to be constructable with a rusty compass by the 17th century, the Poncelet–Steiner theorem proves that the rusty compass and straightedge together are more than sufficient for any and all Euclidean construction.

Alternative scenarios to Poncelet–Steiner

The Poncelet–Steiner theorem requires a circle and its center to be present on the plane. If either one of these is removed, it no longer becomes possible to perform every straightedge-compass construction. Several generalizations of the theorem allow the circle center to be removed or the circle to be relaxed into an incomplete circular arc.

Poncelet–Steiner without the circle center

If the center of the circle is removed, leaving only a single circle on the plane, it is not possible to reconstruct the center using straightedge-only constructions.

This was first proven by David Hilbert using an argument from projective geometry: there exists a projective transformation of the plane to itself such that the given circle is fixed, but the center of the circle is not preserved. The existence of such a transformation means that if a straightedge-only construction for finding the circle center exists, applying the projective transformation would move it to a different point than the center. Hence, such a construction is not possible.^[6]

As a result, a single circle without its center is not sufficient to perform general straightedge-compass constructions. Consequently, the requirements on the Poncelet–Steiner theorem cannot be weakened with respect to the circle center.

However, the center of a circle may be reconstructed as long as sufficient additional information is given on the plane. In each of the following scenarios, it becomes possible to recover the center of a circle, and therefore making every straightedge-compass construction possible:

• one circle and two distinct sets of parallel lines
• one circle and three parallel lines equidistant from each other
• two intersecting or tangent circles^[5][7]
• two concentric circles^[7]
• two circles and a point on the line connecting their centers^[8] or on their radical axis
• two circles and a single set of parallel lines
• two circles that can inscribe and circumscribe a bicentric polygon with an even number of sides^[9]
• three non-intersecting circles not all in the same coaxial system^[5]
• any conic section with its foci (or with the center and one focus)^[10]

Given only two circles without their centers, it is generally not possible to construct their centers using only a straightedge. However, in certain special cases, it is possible, such as when the two circles intersect or are concentric.^[11]

Poncelet–Steiner without a complete circular arc

In 1904, Francesco Severi proved that any small arc (of the circle), together with the centre, will suffice.^[12] Severi's proof illustrates that any arc of the circle fully characterizes the circumference and allows intersection points (of lines) with it to be found, regardless of the absence of some portion of the completed arc. Consequently, the completeness of the circle is not essential, provided an arc and the center are available.

Further generalizations

The Poncelet–Steiner theorem has been generalized to higher dimensions, such as, for example, a three-dimensional variation where the straightedge is replaced with a plane, and the compass is replaced with a sphere. It has been shown that n-dimensional "straightedge and compass" constructions can still be performed using only n-dimensional planes, provided that a single n-dimensional sphere with its center is given.^[13] Many of the properties that apply to the two dimensional case also apply to higher dimensions, as implementations of projective geometry.

Additionally, some research is underway to generalize the Poncelet–Steiner theorem to non-Euclidean geometries.

See also

• Apollonian circles
• Constructible polygon
• Drafting
• Geometric algebra
• Geometric invariant theory
• Geometrography
• Inversive geometry
• Steel square
• T-Square