Top Qs
Timeline
Chat
Perspective
Ramanujan's master theorem
Mathematical theorem From Wikipedia, the free encyclopedia
Remove ads
In mathematics, Ramanujan's master theorem, named after Srinivasa Ramanujan,[1] is a technique that provides an analytic expression for the Mellin transform of an analytic function.
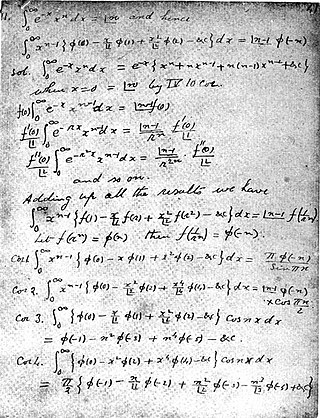
The result is stated as follows:
If a complex-valued function has an expansion of the form
then the Mellin transform of is given by
where is the gamma function.
It was widely used by Ramanujan to calculate definite integrals and infinite series.
Higher-dimensional versions of this theorem also appear in quantum physics through Feynman diagrams.[2]
Remove ads
Alternative formalism
Summarize
Perspective
An alternative formulation of Ramanujan's master theorem is as follows:
which gets converted to the above form after substituting and using the functional equation for the gamma function.
The integral above is convergent for subject to growth conditions on .[4]
Remove ads
Proof
Summarize
Perspective
A proof subject to "natural" assumptions (though not the weakest necessary conditions) to Ramanujan's master theorem was provided by G. H. Hardy[5](chapter XI) employing the residue theorem and the well-known Mellin inversion theorem.
Ramanujan's proof of his master theorem[1] |
|---|
|
Recall Euler's representation of the Gamma function choosing , multiplying both sides by and then summing over to obtain: Observing the sum in the RHS is a Taylor Series and writing in its series expansion:
Rewriting the LHS:
Then once again observing the sum over is a Taylor series: Finally defining and letting we gain the master theorem: |
Remove ads
Application to Bernoulli polynomials
Summarize
Perspective
The generating function of the Bernoulli polynomials is given by:
These polynomials are given in terms of the Hurwitz zeta function:
by for . Using the Ramanujan master theorem and the generating function of Bernoulli polynomials one has the following integral representation:[7]
which is valid for .
Remove ads
Application to the gamma function
Summarize
Perspective
Weierstrass's definition of the gamma function
is equivalent to expression
where is the Riemann zeta function.
Then applying Ramanujan master theorem we have:
valid for .
Special cases of and are
Remove ads
Application to Bessel functions
Summarize
Perspective
The Bessel function of the first kind has the power series
By Ramanujan's master theorem, together with some identities for the gamma function and rearranging, we can evaluate the integral
valid for .
Equivalently, if the spherical Bessel function is preferred, the formula becomes
valid for .
The solution is remarkable in that it is able to interpolate across the major identities for the gamma function. In particular, the choice of gives the square of the gamma function, gives the duplication formula, gives the reflection formula, and fixing to the evaluable or gives the gamma function by itself, up to reflection and scaling.
Remove ads
Bracket integration method
Summarize
Perspective
The bracket integration method (method of brackets) applies Ramanujan's master theorem to a broad range of integrals.[8] The bracket integration method generates the integrand's series expansion, creates a bracket series, identifies the series coefficient and formula parameters and computes the integral.[9]
Integration formulas
This section identifies the integration formulas for integrand's with and without consecutive integer exponents and for single and double integrals. The integration formula for double integrals may be generalized to any multiple integral. In all cases, there is a parameter value or array of parameter values that solves one or more linear equations derived from the exponent terms of the integrand's series expansion.
Consecutive integer exponents, 1 variable
This is the function series expansion, integral and integration formula for an integral whose integrand's series expansion contains consecutive integer exponents.[10] The parameter is a solution to this linear equation.
General exponents, 1 variable
Applying the substitution generates the function series expansion, integral and integration formula for an integral whose integrand's series expansion may not contain consecutive integer exponents.[9] The parameter is a solution to this linear equation.
Consecutive integer exponents, double integral
This is the function series expansion, integral and integration formula for a double integral whose integrand's series expansion contains consecutive integer exponents.[11] The parameters and are solutions to these linear equations.
General exponents, double integral
This section describes the integration formula for a double integral whose integrand's series expansion may not contain consecutive integer exponents. Matrices contain the parameters needed to express the exponents in a series expansion of the integrand, and the determinant of invertible matrix is .[12] Applying the substitution generates the function series expansion, integral and integration formula for a double integral whose integrand's series expansion may not contain consecutive integer exponents.[11] The integral and integration formula are[13][14] The parameter matrix is a solution to this linear equation.[15] .
Positive complexity index
In some cases, there may be more sums then variables. For example, if the integrand is a product of 3 functions of a common single variable, and each function is converted to a series expansion sum, the integrand is now a product of 3 sums, each sum corresponding to a distinct series expansion.
- The number of brackets is the number of linear equations associated with an integral. This term reflects the common practice of bracketing each linear equation.[16]
- The complexity index is the number of integrand sums minus the number of brackets (linear equations). Each series expansion of the integrand contributes one sum.[16]
- The summation indices (variables) are the indices that index terms in a series expansion. In the example, there are 3 summation indices and because the integrand is a product of 3 series expansions.[17]
- The free summation indices (variables) are the summation indices that remain after completing all integrations. Integration reduces the number of sums in the integrand by replacing the series expansions (sums) with an integration formula. Therefore, there are fewer summation indices after integration. The number of chosen free summation indices equals the complexity index.[17]
Integrals with a positive complexity index
The free summation indices are elements of set . The matrix of free summation indices is and the coefficients of the free summation indices is matrix . The remaining indices are set containing indices . Matrices and contain matrix elements that multiply or sum with the non-summation indices. The selected free summation indices must leave matrix non-singular. . This is the function's series expansion, integral and integration formula.[18] The parameters are linear functions of the parameters .[19] .
Bracket series
Bracket series notations are notations that substitute for common power series notations (Table 1).[20] Replacing power series notations with bracket series notations transforms the power series to a bracket series. A bracket series facilitates identifying the formula parameters needed for integration. It is also recommended to replace a sum raised to a power:[20] with this bracket series expression:
Algorithm
This algorithm describes how to apply the integral formulas.[9][10][21]
- Input Integral expression
- Output Integral value or integral cannot be assigned a value
- Express the integrand as a power series.
- Transform the integrand's power series to a bracket series.
- Obtain the complexity index, formula parameters and series coefficient function.
- Complexity index is the number of integrand sums minus number of brackets.
- Parameters or array are solutions to linear equations (zero complexity index, single integral), (zero complexity index, single integral) or (positive complexity index).
- Identify parameter or (zero complexity index, single integral) or compute (all other cases) from the associated linear equations.
- Identify the series coefficient function of the bracket series.
- If the complexity index is negative, return integral cannot be assigned a value.
- If the complexity index is zero, select the formula from table 2 for zero complexity index, single or multiple integral, compute the integral value with this formula, and return this integral value.
- If the complexity index is positive, select the formula from table 2 for positive complexity index, and compute the integral value as a series expansion with this formula for all possible choices of the free summation indices. Select the lowest complexity index, convergent series expansion, adding series that converge in the same region.
- If all series expansions are divergent series or null series (all series terms zero), then return integral cannot be assigned a value.
- If the series expansion is non-null and non-divergent, return this series expansion as the integral value.
Examples
Zero complexity index
The bracket method will integrate this integral.
- Express the integrand as a power series.
- Transform the power series to a bracket series.
- Obtain the complexity index, formula parameters and series coefficient function.
- Complexity index is zero.
- .
- Use table 2 to compute the integral.
Positive complexity index
The bracket method will integrate this integral. 1. Express the integrand as a power series. Use the sum raised to a power formula. 2. Transform the power series to a bracket series. 3. Obtain the complexity index, formula parameters and series coefficient function.
- Complexity index is 1 as 3 sums and 2 brackets.
- Select as the free index, . The linear equations, solutions, determinant and series coefficient are
4. Use table 2 to compute the integral
Remove ads
Citations
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
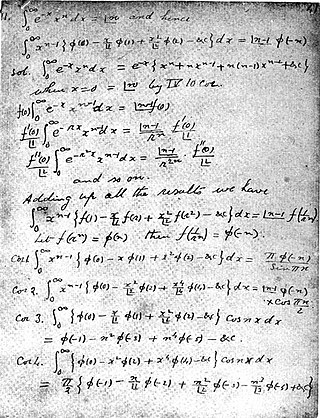





















 ...
...











































































































