Series expansion

In mathematics, a series expansion is a technique that expresses a function as an infinite sum, or series, of simpler functions. It is a method for calculating a function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division).^[1]

An animation showing the cosine function being approximated by successive truncations of its Maclaurin series.

The resulting so-called series often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non-analytic functions.^{[2][verification needed]}

Types of series expansions

There are several kinds of series expansions, listed below.

Taylor series

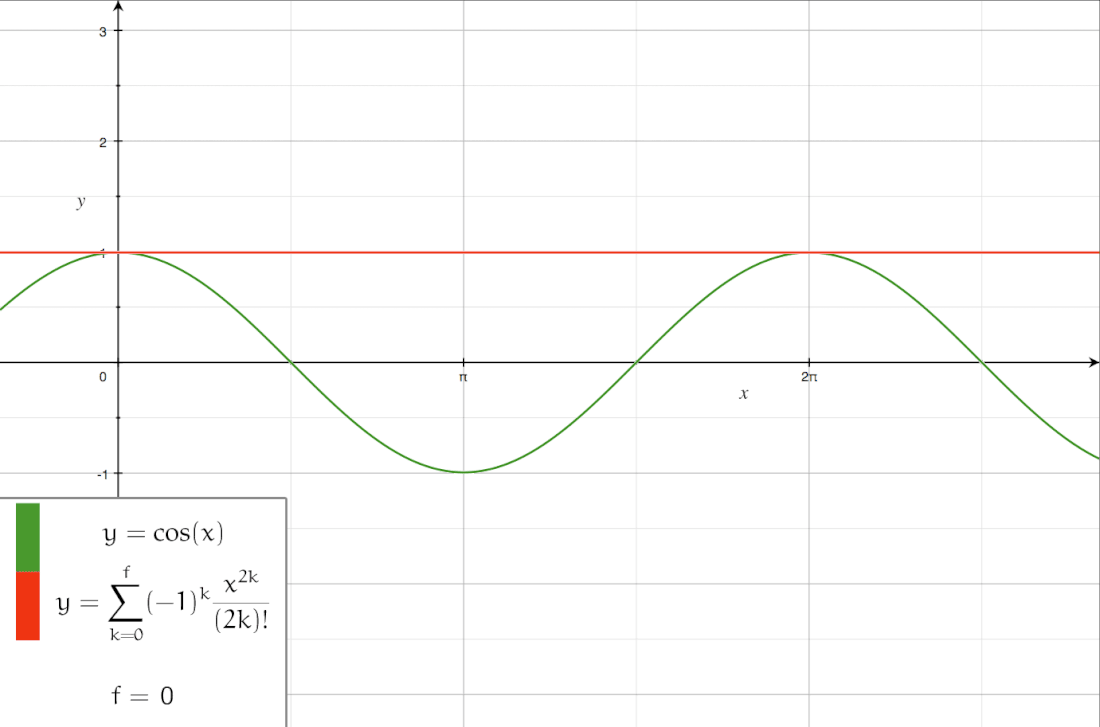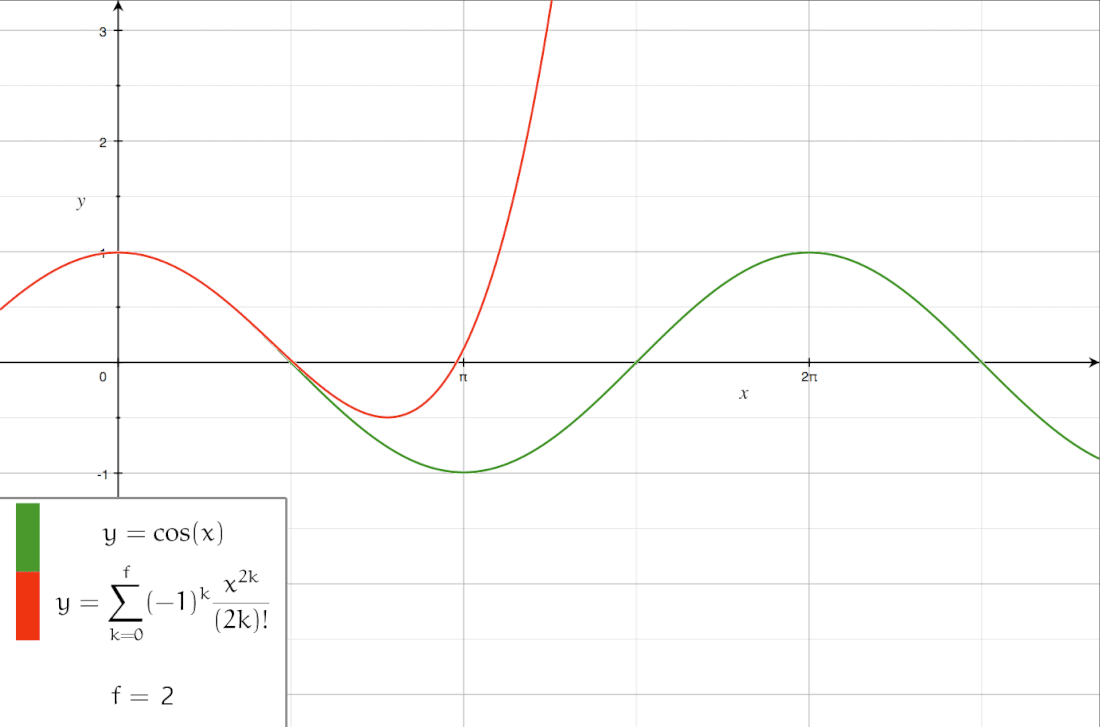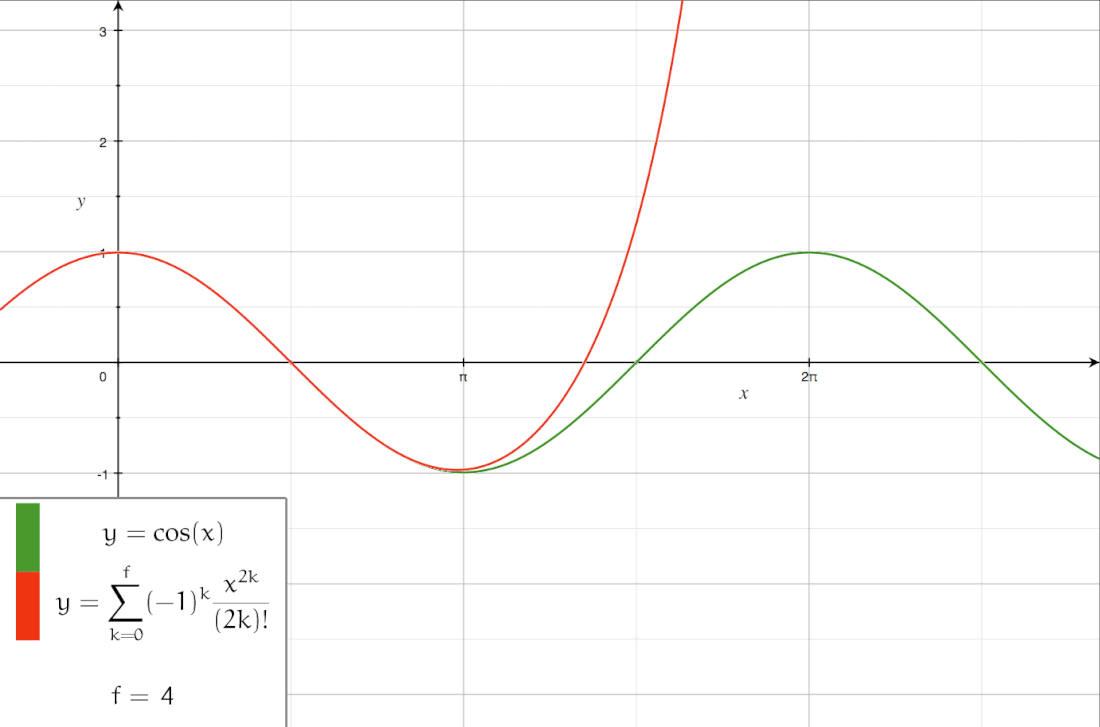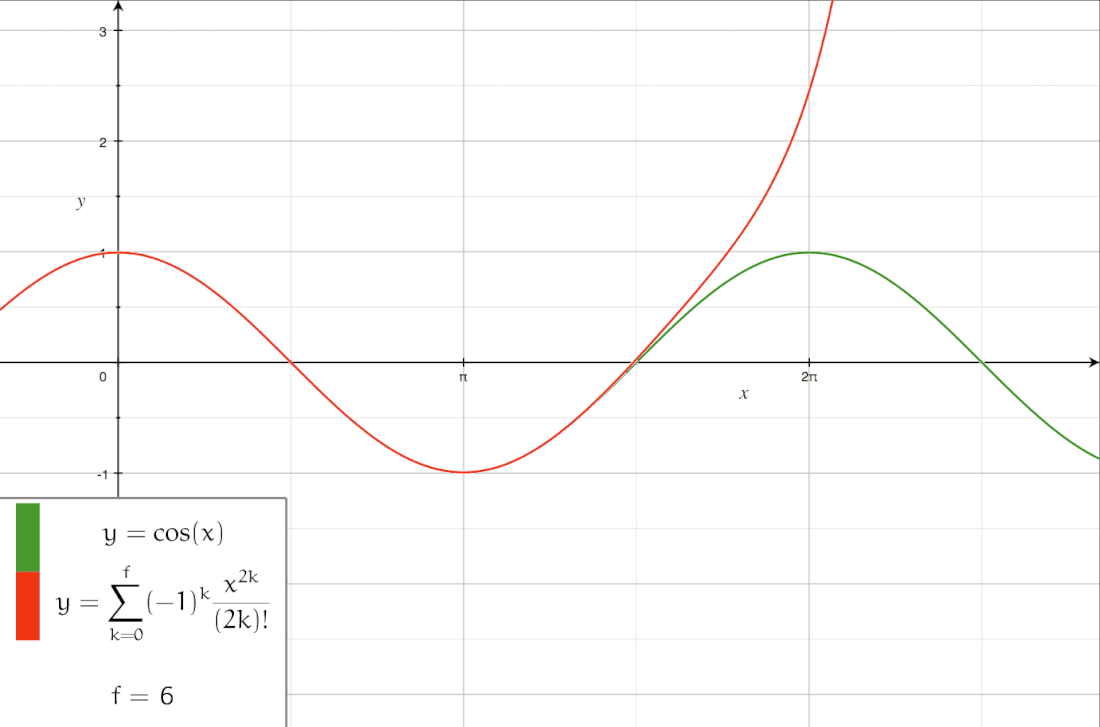
A Taylor series is a power series based on a function's derivatives at a single point.^[3] More specifically, if a function ${\displaystyle f:U\to \mathbb {R} }$ is infinitely differentiable around a point ${\displaystyle x_{0}}$, then the Taylor series of f around this point is given by

${\displaystyle \sum _{n=0}^{\infty }{\frac {f^{(n)}(x_{0})}{n!}}(x-x_{0})^{n}}$

under the convention ${\displaystyle 0^{0}:=1}$.^[3][4] The Maclaurin series of f is its Taylor series about ${\displaystyle x_{0}=0}$.^[5][4]

Laurent series

A Laurent series is a generalization of the Taylor series, allowing terms with negative exponents; it takes the form ${\textstyle \sum _{k=-\infty }^{\infty }c_{k}(z-a)^{k}}$ and converges in an annulus.^[6] In particular, a Laurent series can be used to examine the behavior of a complex function near a singularity by considering the series expansion on an annulus centered at the singularity.

Dirichlet series

Convergence and divergence of partial sums of the Dirichlet series defining the Riemann zeta function. Here, the yellow line represents the first fifty successive partial sums ${\textstyle \sum _{n=1}^{k}n^{-s},}$ the magenta dotted line represents ${\displaystyle {\tfrac {n^{-s+1}}{-s+1}}+\zeta (s),}$ and the green dot represents ${\displaystyle \zeta (s)}$ as s is varied from -0.5 to 1.5.

A general Dirichlet series is a series of the form ${\textstyle \sum _{n=1}^{\infty }a_{n}e^{-\lambda _{n}s}.}$ One important special case of this is the ordinary Dirichlet series ${\textstyle \sum _{n=1}^{\infty }{\frac {a_{n}}{n^{s}}}.}$^[7] Used in number theory.^{[citation needed]}

Fourier series

A Fourier series is an expansion of periodic functions as a sum of many sine and cosine functions.^[8] More specifically, the Fourier series of a function ${\displaystyle f(x)}$ of period ${\displaystyle 2L}$ is given by the expression$${\displaystyle a_{0}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left({\frac {n\pi x}{L}}\right)+b_{n}\sin \left({\frac {n\pi x}{L}}\right)\right]}$$where the coefficients are given by the formulae^[8][9]$${\displaystyle {\begin{aligned}a_{n}&:={\frac {1}{L}}\int _{-L}^{L}f(x)\cos \left({\frac {n\pi x}{L}}\right)dx,\\b_{n}&:={\frac {1}{L}}\int _{-L}^{L}f(x)\sin \left({\frac {n\pi x}{L}}\right)dx.\end{aligned}}}$$

Other series

• In acoustics, e.g., the fundamental tone and the overtones together form an example of a Fourier series.^{[citation needed]}

• Newtonian series^{[citation needed]}

• Legendre polynomials: Used in physics to describe an arbitrary electrical field as a superposition of a dipole field, a quadrupole field, an octupole field, etc.^{[citation needed]}

• Zernike polynomials: Used in optics to calculate aberrations of optical systems. Each term in the series describes a particular type of aberration.^{[citation needed]}

The relative error in a truncated Stirling series vs. n, for 0 to 5 terms. The kinks in the curves represent points where the truncated series coincides with ${\displaystyle \Gamma (n+1).}$

• The Stirling series$${\displaystyle {\text{Ln}}\Gamma \left(z\right)\sim \left(z-{\tfrac {1}{2}}\right)\ln z-z+{\tfrac {1}{2}}\ln \left(2\pi \right)+\sum _{k=1}^{\infty }{\frac {B_{2k}}{2k(2k-1)z^{2k-1}}}}$$is an approximation of the log-gamma function.^[10]

Examples

The following is the Taylor series of ${\displaystyle e^{x}}$:$${\displaystyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}...}$$^[11][12]

The Dirichlet series of the Riemann zeta function is$${\displaystyle \zeta (s):=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+\cdots }$$^[7]