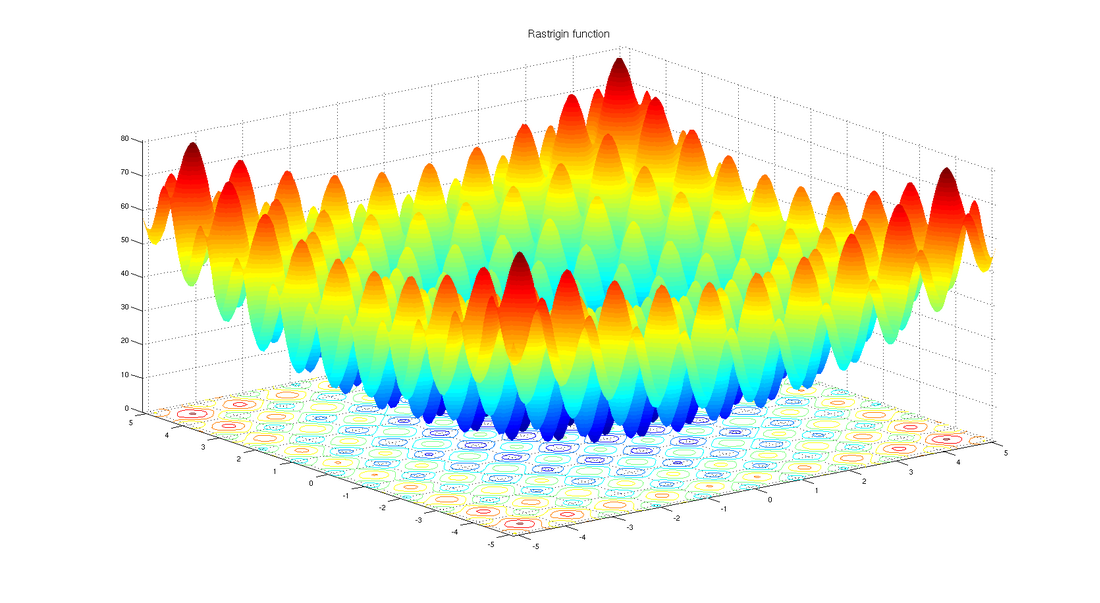
Rastrigin function

In mathematical optimization, the Rastrigin function is a non-convex function used as a performance test problem for optimization algorithms. It is a typical example of non-linear multimodal function. It was first proposed in 1974 by Rastrigin^[1] as a 2-dimensional function and has been generalized by Rudolph.^[2] The generalized version was popularized by Hoffmeister & Bäck^[3] and Mühlenbein et al.^[4] Finding the minimum of this function is a fairly difficult problem due to its large search space and its large number of local minima.

Rastrigin function of two variables

In 3D

Contour

On an ${\displaystyle n}$-dimensional domain it is defined by:

${\displaystyle f(\mathbf {x} )=An+\sum _{i=1}^{n}\left[x_{i}^{2}-A\cos(2\pi x_{i})\right]}$

where ${\displaystyle A=10}$ and ${\displaystyle x_{i}\in [-5.12,5.12]}$. There are many extrema:

• The global minimum is at ${\displaystyle \mathbf {x} =\mathbf {0} }$ where ${\displaystyle f(\mathbf {x} )=0}$.
• The maximum function value for ${\displaystyle x_{i}\in [-5.12,5.12]}$ is located at ${\displaystyle \mathbf {x} =(\pm 4.52299366...,...,\pm 4.52299366...)}$:

Number of dimensions	Maximum value at ${\displaystyle \pm 4.52299366}$
1	40.35329019
2	80.70658039
3	121.0598706
4	161.4131608
5	201.7664509
6	242.1197412
7	282.4730314
8	322.8263216
9	363.1796117

Here are all the values at 0.5 interval listed for the 2D Rastrigin function with ${\displaystyle x_{i}\in [-5.12,5.12]}$:

${\displaystyle f(x)}$		${\displaystyle x_{1}}$
		${\displaystyle 0}$	${\displaystyle \pm 0.5}$	${\displaystyle \pm 1}$	${\displaystyle \pm 1.5}$	${\displaystyle \pm 2}$	${\displaystyle \pm 2.5}$	${\displaystyle \pm 3}$	${\displaystyle \pm 3.5}$	${\displaystyle \pm 4}$	${\displaystyle \pm 4.5}$	${\displaystyle \pm 5}$	${\displaystyle \pm 5.12}$
${\displaystyle x_{2}}$	${\displaystyle 0}$	0	20.25	1	22.25	4	26.25	9	32.25	16	40.25	25	28.92
	${\displaystyle \pm 0.5}$	20.25	40.5	21.25	42.5	24.25	46.5	29.25	52.5	36.25	60.5	45.25	49.17
	${\displaystyle \pm 1}$	1	21.25	2	23.25	5	27.25	10	33.25	17	41.25	26	29.92
	${\displaystyle \pm 1.5}$	22.25	42.5	23.25	44.5	26.25	48.5	31.25	54.5	38.25	62.5	47.25	51.17
	${\displaystyle \pm 2}$	4	24.25	5	26.25	8	30.25	13	36.25	20	44.25	29	32.92
	${\displaystyle \pm 2.5}$	26.25	46.5	27.25	48.5	30.25	52.5	35.25	58.5	42.25	66.5	51.25	55.17
	${\displaystyle \pm 3}$	9	29.25	10	31.25	13	35.25	18	41.25	25	49.25	34	37.92
	${\displaystyle \pm 3.5}$	32.25	52.5	33.25	54.5	36.25	58.5	41.25	64.5	48.25	72.5	57.25	61.17
	${\displaystyle \pm 4}$	16	36.25	17	38.25	20	42.25	25	48.25	32	56.25	41	44.92
	${\displaystyle \pm 4.5}$	40.25	60.5	41.25	62.5	44.25	66.5	49.25	72.5	56.25	80.5	65.25	69.17
	${\displaystyle \pm 5}$	25	45.25	26	47.25	29	51.25	34	57.25	41	65.25	50	53.92
	${\displaystyle \pm 5.12}$	28.92	49.17	29.92	51.17	32.92	55.17	37.92	61.17	44.92	69.17	53.92	57.85

The abundance of local minima underlines the necessity of a global optimization algorithm when needing to find the global minimum. Local optimization algorithms are likely to get stuck in a local minimum.

See also

• Test functions for optimization