Riemann surface

In mathematics, particularly in complex analysis, a Riemann surface is a connected one-dimensional complex manifold. These surfaces were first studied by and are named after Bernhard Riemann. Riemann surfaces can be thought of as deformed versions of the complex plane: locally near every point they look like patches of the complex plane, but the global topology can be quite different. For example, they can look like a sphere or a torus or several sheets glued together.

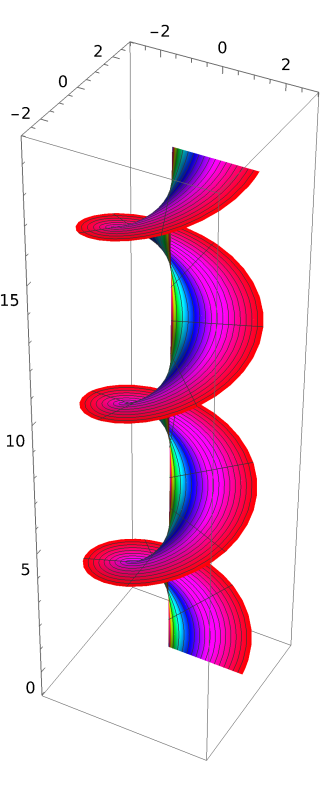
The main interest in Riemann surfaces is that holomorphic functions may be defined between them. Riemann surfaces are nowadays considered the natural setting for studying the global behavior of these functions, especially multi-valued functions such as the square root and other algebraic functions, or the logarithm.

Every Riemann surface is a two-dimensional real analytic manifold (i.e., a surface), but it contains more structure (specifically a complex structure) which is needed for the unambiguous definition of holomorphic functions. A two-dimensional real manifold can be turned into a Riemann surface (usually in several inequivalent ways) if and only if it is orientable and metrizable. So the sphere and torus admit complex structures, but the Möbius strip, Klein bottle and real projective plane do not.

Geometrical facts about Riemann surfaces are as "nice" as possible, and they often provide the intuition and motivation for generalizations to other curves, manifolds or varieties. The Riemann–Roch theorem is a prime example of this influence.