Top Qs
Timeline
Chat
Perspective
Right-hand rule
Mnemonic for understanding orientation of vectors in 3D space From Wikipedia, the free encyclopedia
Remove ads
In mathematics and physics, the right-hand rule is a convention and a mnemonic, utilized to define the orientation of axes in three-dimensional space and to determine the direction of the cross product of two vectors, as well as to establish the direction of the force on a current-carrying conductor in a magnetic field.
The various right- and left-hand rules arise from the fact that the three axes of three-dimensional space have two possible orientations. This can be seen by holding your hands together with palms up and fingers curled. If the curl of the fingers represents a movement from the first or x-axis to the second or y-axis, then the third or z-axis can point along either right thumb or left thumb.
Remove ads
History
Summarize
Perspective
The right-hand rule dates back to the 19th century when it was implemented as a way for identifying the positive direction of coordinate axes in three dimensions. William Rowan Hamilton, recognized for his development of quaternions, a mathematical system for representing three-dimensional rotations, is often attributed with the introduction of this convention. In the context of quaternions, the Hamiltonian product of two vector quaternions yields a quaternion comprising both scalar and vector components.[1] Josiah Willard Gibbs recognized that treating these components separately, as dot and cross product, simplifies vector formalism. Following a substantial debate,[2] the mainstream shifted from Hamilton's quaternionic system to Gibbs' three-vectors system. This transition led to the prevalent adoption of the right-hand rule in the contemporary contexts. In specific, Gibbs outlines his intention for establishing a right-handed coordinate system in his pamphlet on vector analysis.[3] In Article 11 of the pamphlet, Gibbs states "The letters , , and are appropriated to the designation of a normal system of unit vectors, i.e., three unit vectors, each of which is at right angles to the other two ... We shall always suppose that is on the side of the plane on which a rotation from to (through one right angle) appears counter-clockwise." While Gibbs did not use the term right-handed in his discussion, his instructions for defining the normal coordinate orientation are a clear statement of his intent for coordinates that follow the right-hand rule.

The cross product of vectors and is a vector perpendicular to the plane spanned by and with the direction given by the right-hand rule: If you put the index of your right hand on and the middle finger on , then the thumb points in the direction of .[4]

The right-hand rule in physics was introduced in the late 19th century by John Fleming in his book Magnets and Electric Currents.[5] Fleming described the orientation of the induced electromotive force by referencing the motion of the conductor and the direction of the magnetic field in the following depiction: “If a conductor, represented by the middle finger, be moved in a field of magnetic flux, the direction of which is represented by the direction of the forefinger, the direction of this motion, being in the direction of the thumb, then the electromotive force set up in it will be indicated by the direction in which the middle finger points."[5]
Remove ads
Coordinates
Summarize
Perspective

right-handed coordinates on the right.
For right-handed coordinates, if the thumb of a person's right hand points along the z-axis in the positive direction (third coordinate vector), then the fingers curl from the positive x-axis (first coordinate vector) toward the positive y-axis (second coordinate vector). When viewed at a position along the positive z-axis, the ¼ turn from the positive x- to the positive y-axis is counter-clockwise.
For left-handed coordinates, the above description of the axes is the same, except using the left hand; and the ¼ turn is clockwise.
Interchanging the labels of any two axes reverses the handedness. Reversing the direction of one axis (or three axes) also reverses the handedness. Reversing two axes amounts to a 180° rotation around the remaining axis, also preserving the handedness. These operations can be composed to give repeated changes of handedness.[6] (If the axes do not have a positive or negative direction, then handedness has no meaning.)
Remove ads
Rotations
Summarize
Perspective
A rotating body

In mathematics, a rotating body is commonly represented by a pseudovector along the axis of rotation. The length of the vector gives the speed of rotation and the direction of the axis gives the direction of rotation according to the right-hand rule: right fingers curled in the direction of rotation and the right thumb pointing in the positive direction of the axis. This allows some simple calculations using the vector cross-product. No part of the body is moving in the direction of the axis arrow. If the thumb is pointing north, Earth rotates according to the right-hand rule (prograde motion). This causes the Sun, Moon, and stars to appear to revolve westward according to the left-hand rule.
Helixes and screws

A helix is a curved line formed by a point rotating around a center while the center moves up or down the z-axis. Helices are either right or left handed with curled fingers giving the direction of rotation and thumb giving the direction of advance along the z-axis.
The threads of a screw are helical and therefore screws can be right- or left-handed. To properly fasten or unfasten a screw, one applies the above rules: if a screw is right-handed, pointing one's right thumb in the direction of the hole and turning in the direction of the right hand's curled fingers (i.e. clockwise) will fasten the screw, while pointing away from the hole and turning in the new direction (i.e. counterclockwise) will unfasten the screw.
Curve orientation and normal vectors
In vector calculus, it is necessary to relate a normal vector of a surface to the boundary curve of the surface. Given a surface S with a specified normal direction n̂ (a choice of "upward direction" with respect to S), the boundary curve C around S is defined to be positively oriented provided that the right thumb points in the direction of n̂ and the fingers curl along the orientation of the bounding curve C.
Remove ads
Electromagnetism
Summarize
Perspective
- When electricity flows (with direction given by conventional current) in a long straight wire, it creates a cylindrical magnetic field around the wire according to the right-hand rule. The conventional direction of a magnetic line is given by a compass needle.
- Electromagnet: The magnetic field around a wire is relatively weak. If the wire is coiled into a helix, all the field lines inside the helix point in the same direction and each successive coil reinforces the others. The advance of the helix, the non-circular part of the current, and the field lines all point in the positive z direction. Since there is no magnetic monopole, the field lines exit the +z end, loop around outside the helix, and re-enter at the −z end. The +z end where the lines exit is defined as the north pole. If the fingers of the right hand are curled in the direction of the circular component of the current, the right thumb points to the north pole.
- Lorentz force: If an electric charge moves across a magnetic field, it experiences a force according to the Lorentz force, with the direction given by the right-hand rule. If the index finger represents the direction of flow of charge (i.e. the current) and the middle finger represents the direction of the magnetic field in space, the direction of the force on the charge is represented by the thumb. Because the charge is moving, the force causes the particle path to bend. The bending force is computed by the vector cross-product. This means that the bending force increases with the velocity of the particle and the strength of the magnetic field. The force is maximum when the particle direction and magnetic fields are perpendicular, is less at any other angle, and is zero when the particle moves parallel to the field.
Ampère's right-hand grip rule
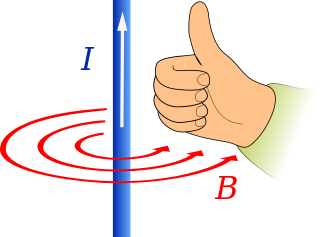

Ampère's right-hand grip rule,[7] also called the right-hand screw rule, coffee-mug rule or the corkscrew-rule; is used either when a vector (such as the Euler vector) must be defined to represent the rotation of a body, a magnetic field, or a fluid, or vice versa, when it is necessary to define a rotation vector to understand how rotation occurs. It reveals a connection between the current and the magnetic field lines in the magnetic field that the current created. Ampère was inspired by fellow physicist Hans Christian Ørsted, who observed that needles swirled when in the proximity of an electric current-carrying wire and concluded that electricity could create magnetic fields.
Application
This rule is used in two different applications of Ampère's circuital law:
- To determine the direction of the magnetic flux around the conductor. The direction of the magnetic field (counterclockwise rotation instead of clockwise rotation of coordinates when viewing the tip of the thumb) is a result of this convention and not an underlying physical phenomenon
- The Right-Hand Thumb Rule: Describes the magnetic field around a current-carrying conductor. When electric current passes through a straight wire, point the thumb of your right hand in the direction of the conventional current (from positive to negative). The curled fingers will then point in the direction of the magnetic flux lines around the conductor.
- The Right-Hand Screw Rule (Maxwell’s Corkscrew Rule): This rule helps determine the direction of the magnetic field. If you imagine screwing a right-handed screw in the direction of the conventional current (from positive to negative), the direction the screw moves indicates the magnetic field. The field direction follows a counterclockwise rotation of coordinates when viewed from the tip of the thumb, based on this convention.
- To determine the direction of the magnetic north pole in a Solenoid.
- An electric current passes through a solenoid, resulting in a magnetic field. When wrapping the right hand around the solenoid with the fingers in the direction of the conventional current, the thumb points in the direction of the magnetic north pole.
Remove ads
Cross products
Summarize
Perspective

The cross product of two vectors is often taken in physics and engineering. For example, as discussed above, the force exerted on a moving charged particle when moving in a magnetic field B is given by the magnetic term of Lorentz force:
- (vector cross product)
The direction of the cross product may be found by application of the right-hand rule as follows:
- The index finger points in the direction of the velocity vector v.
- The middle finger points in the direction of the magnetic field vector B.
- The thumb points in the direction of the cross product F.
For example, for a positively charged particle moving to the north, in a region where the magnetic field points west, the resultant force points up.[6]
Applications
The right-hand rule has widespread use in physics. A list of physical quantities whose directions are related by the right-hand rule is given below. (Some of these are related only indirectly to cross products, and use the second form.)
- For a rotating object, if the right-hand fingers follow the curve of a point on the object, then the thumb points along the axis of rotation in the direction of the angular velocity vector.
- A torque, the force that causes it, and the position of the point of application of the force.
- A magnetic field, the position of the point where it is determined, and the electric current (or change in electric flux) that causes it.
- A magnetic field in a coil of wire and the electric current in the wire.
- The force of a magnetic field on a charged particle, the magnetic field itself, and the velocity of the object.
- The vorticity at any point in the field of the flow of a fluid
- The induced current from motion in a magnetic field (known as Fleming's right-hand rule).
- The x, y and z unit vectors in a Cartesian coordinate system can be chosen to follow the right-hand rule. Right-handed coordinate systems are often used in rigid body and kinematics.
Remove ads
Meta-mathematical issues
Unlike most mathematical concepts, the meaning of a right-handed coordinate system cannot be expressed in terms of any mathematical axioms. Rather, the definition depends on chiral phenomena in the physical world, for example the culturally transmitted meaning of right and left hands, a majority human population with dominant right hand, or certain phenomena involving the weak force.
See also
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads







