Top Qs
Timeline
Chat
Perspective
Selection sort
Sorting algorithm From Wikipedia, the free encyclopedia
Remove ads
In computer science, selection sort is an in-place comparison sorting algorithm. It has a O(n2) time complexity, which makes it inefficient on large lists, and generally performs worse than the similar insertion sort. Selection sort is noted for its simplicity and has performance advantages over more complicated algorithms in certain situations, particularly where auxiliary memory is limited.
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (May 2019) |
The algorithm divides the input list into two parts: a sorted sublist of items which is built up from left to right at the front (left) of the list and a sublist of the remaining unsorted items that occupy the rest of the list. Initially, the sorted sublist is empty and the unsorted sublist is the entire input list. The algorithm proceeds by finding the smallest (or largest, depending on sorting order) element in the unsorted sublist, exchanging (swapping) it with the leftmost unsorted element (putting it in sorted order), and moving the sublist boundaries one element to the right.
The time efficiency of selection sort is quadratic, so there are a number of sorting techniques which have better time complexity than selection sort.
Remove ads
Example
Summarize
Perspective
Here is an example of this sort algorithm sorting five elements:
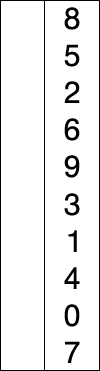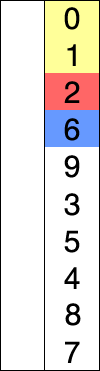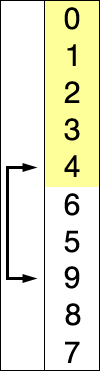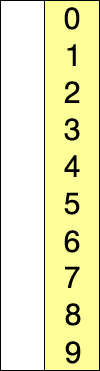
(Nothing appears changed on these last two lines because the last two numbers were already in order.)
Selection sort can also be used on list structures that make add and remove efficient, such as a linked list. In this case it is more common to remove the minimum element from the remainder of the list, and then insert it at the end of the values sorted so far. For example:
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning <11> 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 <12> 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 <22> 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 <25> 64
Remove ads
Implementations
Below is an implementation in C.
/* a[0] to a[aLength-1] is the array to sort */
int i,j;
int aLength; // initialise to a's length
/* advance the position through the entire array */
/* (could do i < aLength-1 because single element is also min element) */
for (i = 0; i < aLength-1; i++)
{
/* find the min element in the unsorted a[i .. aLength-1] */
/* assume the min is the first element */
int jMin = i;
/* test against elements after i to find the smallest */
for (j = i+1; j < aLength; j++)
{
/* if this element is less, then it is the new minimum */
if (a[j] < a[jMin])
{
/* found new minimum; remember its index */
jMin = j;
}
}
if (jMin != i)
{
swap(&a[i], &a[jMin]);
}
}
Remove ads
Complexity
Summarize
Perspective
Selection sort is not difficult to analyze compared to other sorting algorithms, since none of the loops depend on the data in the array. Selecting the minimum requires scanning elements (taking comparisons) and then swapping it into the first position. Finding the next lowest element requires scanning the remaining elements (taking comparisons) and so on. Therefore, the total number of comparisons is
which is of complexity in terms of number of comparisons.
Remove ads
Comparison to other sorting algorithms
Summarize
Perspective
Among quadratic sorting algorithms (sorting algorithms with a simple average-case of Θ(n2)), selection sort almost always outperforms bubble sort and gnome sort. Insertion sort is very similar in that after the kth iteration, the first elements in the array are in sorted order. Insertion sort's advantage is that it only scans as many elements as it needs in order to place the st element, while selection sort must scan all remaining elements to find the st element.
Simple calculation shows that insertion sort will therefore usually perform about half as many comparisons as selection sort, although it can perform just as many or far fewer depending on the order the array was in prior to sorting. It can be seen as an advantage for some real-time applications that selection sort will perform identically regardless of the order of the array, while insertion sort's running time can vary considerably. However, this is more often an advantage for insertion sort in that it runs much more efficiently if the array is already sorted or "close to sorted."
While selection sort is preferable to insertion sort in terms of number of writes ( swaps versus up to swaps, with each swap being two writes), this is roughly twice the theoretical minimum achieved by cycle sort, which performs at most n writes. This can be important if writes are significantly more expensive than reads, such as with EEPROM or Flash memory, where every write lessens the lifespan of the memory.
Selection sort can be implemented without unpredictable branches for the benefit of CPU branch predictors, by finding the location of the minimum with branch-free code and then performing the swap unconditionally.
Finally, selection sort is greatly outperformed on larger arrays by divide-and-conquer algorithms such as mergesort. However, insertion sort or selection sort are both typically faster for small arrays (i.e. fewer than 10–20 elements). A useful optimization in practice for the recursive algorithms is to switch to insertion sort or selection sort for "small enough" sublists.
Remove ads
Variants
Summarize
Perspective
Heapsort has been described as "nothing but an implementation of selection sort using the right data structure."[1] It greatly improves the basic algorithm by using an implicit heap data structure to find and remove each lowest element in time, instead of normal selection sort's inner loop, reducing the total running time to .
A bidirectional variant of selection sort (called double selection sort or sometimes cocktail sort due to its similarity to cocktail shaker sort) finds both the minimum and maximum values in the list in every pass. This requires three comparisons per two items (a pair of elements is compared, then the greater is compared to the maximum and the lesser is compared to the minimum) rather than regular selection sort's one comparison per item, but requires only half as many passes, a net 25% savings.
Selection sort can be implemented as a stable sort if, rather than swapping in step 2, the minimum value is inserted into the first position and the intervening values shifted up. However, this modification either requires a data structure that supports efficient insertions or deletions, such as a linked list, or it leads to performing writes.
In the bingo sort variant, items are sorted by repeatedly looking through the remaining items to find the greatest value and moving all items with that value to their final location.[2] Like counting sort, this is an efficient variant if there are many duplicate values: selection sort does one pass through the remaining items for each item moved, while Bingo sort does one pass for each value. After an initial pass to find the greatest value, subsequent passes move every item with that value to its final location while finding the next value as in the following pseudocode (arrays are zero-based and the for-loop includes both the top and bottom limits, as in Pascal):
bingo(array A)
{ This procedure sorts in ascending order by
repeatedly moving maximal items to the end. }
begin
last := length(A) - 1;
{ The first iteration is written to look very similar to
the subsequent ones, but without swaps. }
nextMax := A[last];
for i := last - 1 downto 0 do
if A[i] > nextMax then
nextMax := A[i];
while (last > 0) and (A[last] = nextMax) do
last := last - 1;
while last > 0 do begin
{ Each main loop searches for the new nextMax while
swapping items equal to prevMax into place. }
prevMax := nextMax;
nextMax := A[last];
for i := last - 1 downto 0 do
if A[i] > nextMax then
if A[i] <> prevMax then
nextMax := A[i];
else begin
swap(A[i], A[last]);
last := last - 1;
end
while (last > 0) and (A[last] = nextMax) do
last := last - 1;
end;
end;
Thus, if on average there are more than two items with the same value, bingo sort can be expected to be faster because it executes the inner loop fewer times than selection sort.
Remove ads
See also
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads














