Top Qs
Timeline
Chat
Perspective
Singularity theory
Mathematical theory From Wikipedia, the free encyclopedia
Remove ads
In mathematics, singularity theory studies spaces that are almost manifolds, but not quite. A string can serve as an example of a one-dimensional manifold, if one neglects its thickness. A singularity can be made by balling it up, dropping it on the floor, and flattening it. In some places the flat string will cross itself in an approximate "X" shape. The points on the floor where it does this are one kind of singularity, the double point: one bit of the floor corresponds to more than one bit of string. Perhaps the string will also touch itself without crossing, like an underlined "U". This is another kind of singularity. Unlike the double point, it is not stable, in the sense that a small push will lift the bottom of the "U" away from the "underline".
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
Vladimir Arnold defines the main goal of singularity theory as describing how objects depend on parameters, particularly in cases where the properties undergo sudden change under a small variation of the parameters. These situations are called perestroika (Russian: перестройка), bifurcations or catastrophes. Classifying the types of changes and characterizing sets of parameters which give rise to these changes are some of the main mathematical goals. Singularities can occur in a wide range of mathematical objects, from matrices depending on parameters to wavefronts.[1]
Remove ads
How singularities may arise
In singularity theory the general phenomenon of points and sets of singularities is studied, as part of the concept that manifolds (spaces without singularities) may acquire special, singular points by a number of routes. Projection is one way, very obvious in visual terms when three-dimensional objects are projected into two dimensions (for example in one of our eyes); in looking at classical statuary the folds of drapery are amongst the most obvious features. Singularities of this kind include caustics, very familiar as the light patterns at the bottom of a swimming pool.
Other ways in which singularities occur is by degeneration of manifold structure. The presence of symmetry can be good cause to consider orbifolds, which are manifolds that have acquired "corners" in a process of folding up, resembling the creasing of a table napkin.
Remove ads
Singularities in algebraic geometry
Summarize
Perspective
Algebraic curve singularities
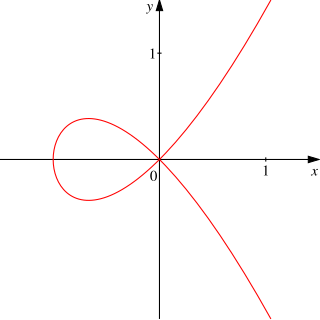

Historically, singularities were first noticed in the study of algebraic curves. The double point at (0, 0) of the curve
and the cusp there of
are qualitatively different, as is seen just by sketching. Isaac Newton carried out a detailed study of all cubic curves, the general family to which these examples belong. It was noticed in the formulation of Bézout's theorem that such singular points must be counted with multiplicity (2 for a double point, 3 for a cusp), in accounting for intersections of curves.
It was then a short step to define the general notion of a singular point of an algebraic variety; that is, to allow higher dimensions.
The general position of singularities in algebraic geometry
Such singularities in algebraic geometry are the easiest in principle to study, since they are defined by polynomial equations and therefore in terms of a coordinate system. One can say that the extrinsic meaning of a singular point isn't in question; it is just that in intrinsic terms the coordinates in the ambient space don't straightforwardly translate the geometry of the algebraic variety at the point. Intensive studies of such singularities led in the end to Heisuke Hironaka's fundamental theorem on resolution of singularities (in birational geometry in characteristic 0). This means that the simple process of "lifting" a piece of string off itself, by the "obvious" use of the cross-over at a double point, is not essentially misleading: all the singularities of algebraic geometry can be recovered as some sort of very general collapse (through multiple processes). This result is often implicitly used to extend affine geometry to projective geometry: it is entirely typical for an affine variety to acquire singular points on the hyperplane at infinity, when its closure in projective space is taken. Resolution says that such singularities can be handled rather as a (complicated) sort of compactification, ending up with a compact manifold (for the strong topology, rather than the Zariski topology, that is).
Remove ads
The smooth theory and catastrophes
Summarize
Perspective
At about the same time as Hironaka's work, the catastrophe theory of René Thom was receiving a great deal of attention. This is another branch of singularity theory, based on earlier work of Hassler Whitney on critical points. Roughly speaking, a critical point of a smooth function is where the level set develops a singular point in the geometric sense. This theory deals with differentiable functions in general, rather than just polynomials. To compensate, only the stable phenomena are considered. One can argue that in nature, anything destroyed by tiny changes is not going to be observed; the visible is the stable. Whitney had shown that in low numbers of variables the stable structure of critical points is very restricted, in local terms. Thom built on this, and his own earlier work, to create a catastrophe theory supposed to account for discontinuous change in nature.
Arnold's view
While Thom was an eminent mathematician, the subsequent fashionable nature of elementary catastrophe theory as propagated by Christopher Zeeman caused a reaction, in particular on the part of Vladimir Arnold.[2] He may have been largely responsible for applying the term singularity theory to the area including the input from algebraic geometry, as well as that flowing from the work of Whitney, Thom and other authors. He wrote in terms making clear his distaste for the too-publicised emphasis on a small part of the territory. The foundational work on smooth singularities is formulated as the construction of equivalence relations on singular points, and germs. Technically this involves group actions of Lie groups on spaces of jets; in less abstract terms Taylor series are examined up to change of variable, pinning down singularities with enough derivatives. Applications, according to Arnold, are to be seen in symplectic geometry, as the geometric form of classical mechanics.
Duality
An important reason why singularities cause problems in mathematics is that, with a failure of manifold structure, the invocation of Poincaré duality is also disallowed. A major advance was the introduction of intersection cohomology, which arose initially from attempts to restore duality by use of strata. Numerous connections and applications stemmed from the original idea, for example the concept of perverse sheaf in homological algebra.
Remove ads
Other possible meanings
The theory mentioned above does not directly relate to the concept of mathematical singularity as a value at which a function is not defined. For that, see for example isolated singularity, essential singularity, removable singularity. The monodromy theory of differential equations, in the complex domain, around singularities, does however come into relation with the geometric theory. Roughly speaking, monodromy studies the way a covering map can degenerate, while singularity theory studies the way a manifold can degenerate; and these fields are linked.
Remove ads
See also
Notes
References
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads

