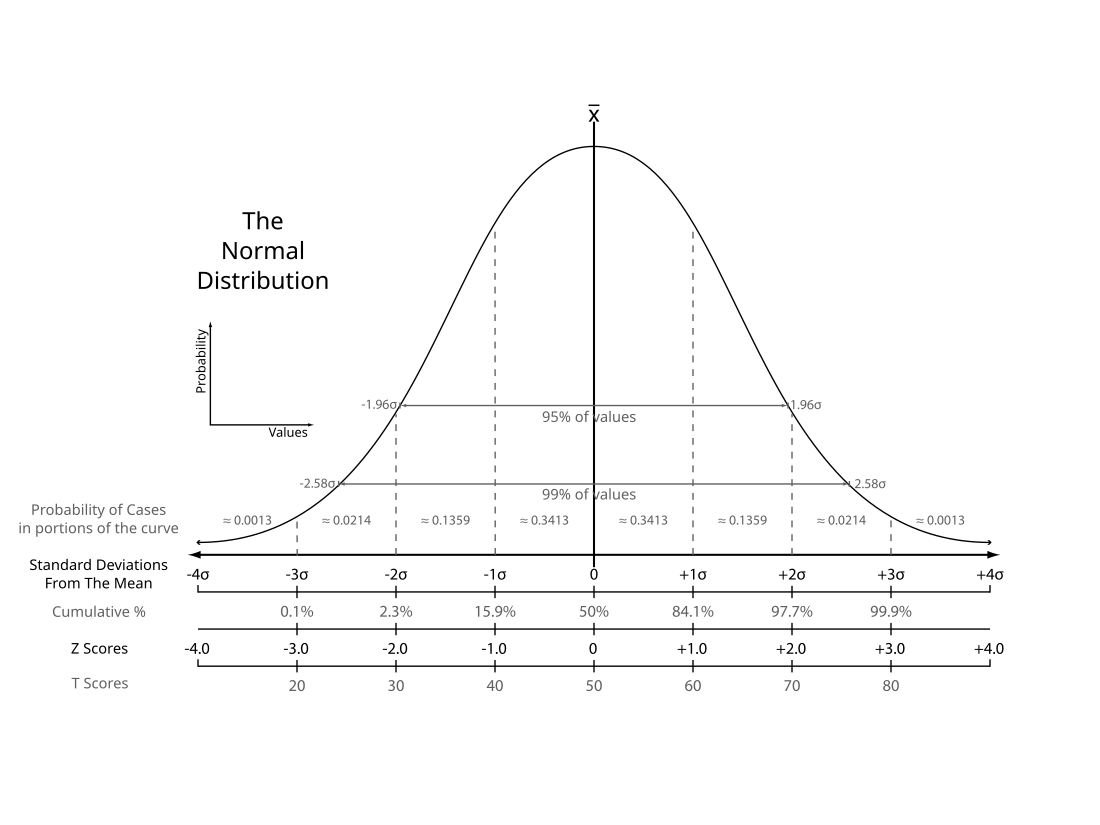
Standard score

In statistics, the standard score is the number of standard deviations by which the value of a raw score (i.e., an observed value or data point) is above or below the mean value of what is being observed or measured. Raw scores above the mean have positive standard scores, while those below the mean have negative standard scores.

It is calculated by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation. This process of converting a raw score into a standard score is called standardizing or normalizing (however, "normalizing" can refer to many types of ratios; see normalization for more).

Standard scores are most commonly called z-scores; the two terms may be used interchangeably, as they are in this article. Other equivalent terms in use include z-values, normal scores, standardized variables and pull in high energy physics.[1][2]

Computing a z-score requires knowledge of the mean and standard deviation of the complete population to which a data point belongs; if one only has a sample of observations from the population, then the analogous computation using the sample mean and sample standard deviation yields the t-statistic.